解析有缺口效应的K值求解方法

1.缺口应力估算

如先前所讨论，自平衡应力反映了缺口效应的响应，且不影响假定裂纹平面的整体平衡（图6-2中A—A截面）。但是当裂纹无限小时的应力状态下，自平衡的应力分布将扩大局部应力强度从而影响裂纹的扩展。

为了使自平衡的应力状态与应力强度因子求解相联系，利用平衡原理，在假定的裂纹面上（实际并不存在），定义等效的裂纹面上的应力p_m和p_b。为了实现这一目的，假定由缺口引起的自平衡应力可以根据具有任意裂纹深度l（图6-2），且以p_m和p_b表示的等效平衡应力得到，如图6-2中任意给定的裂纹深度l，可以通过σ^t_m、σ^t_b、σ_m和σ_b在另外的交叉区域重新分配而完成对p_m和p_b的计算。a_l=l/t表示相对裂纹，省略中间推导过程后可以得到：

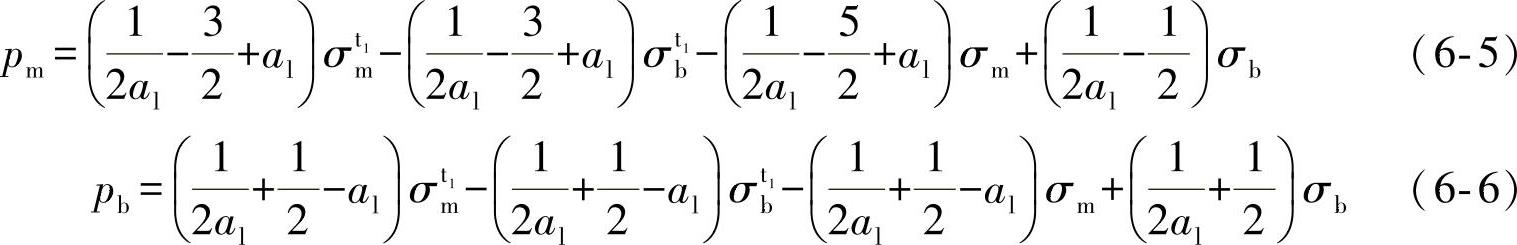
这样缺口应力的自平衡条件就因此而被保留下来。

2.具有缺口效应的应力强度因子

如上面所讨论的缺口应力具有假定裂纹面（图6-2）的应力自平衡的特点，在断裂力学的文章中被表达为式（6-5）和式（6-6）。设a=1，并用式（6-1）和二维板边裂纹试样有关的叠加方法，于是包括缺口效应Ⅰ模式（张开型）的应力强度因子在任意给定的裂纹大小为a的情况下其表达式为(www.xing528.com)

p_s=p_m+p_b，r_l=p_b/p_s。

同样，对于椭圆裂纹，缺口应力强度因子可表达为

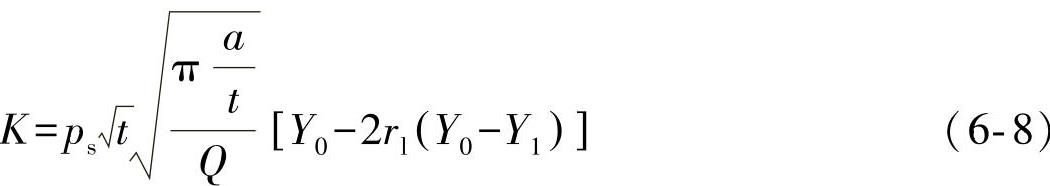
p_m和p_b已经在式（6-5）和式（6-6）中给出。