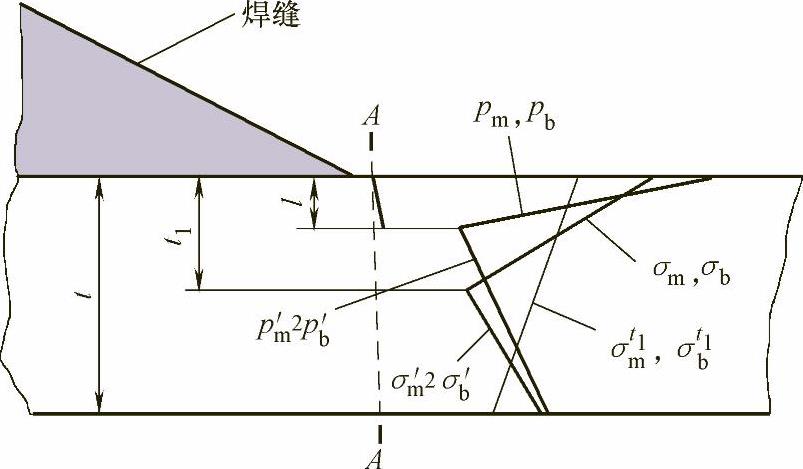
【摘要】:结构应力K估值为通用的K估值提供了便利方法,下面将分别考虑两种情况:板边裂纹的K值求解和椭圆裂纹的K值求解。如先前所讨论,σtm和σtb表示远场的结构应力分量,认为与整个厚度t上的定义有关,如图6-2所示。图6-2 沿厚度方向自平衡的应力对小裂纹应力强度因子的影响2.椭圆裂纹形态下的K值求解一旦获得结构应力分量,相应的椭圆裂纹K值求解就可以通过和板边裂纹K值求解一样的方法建立。
这部分内容是要建立通用的K估值方法,以使它能用于几乎所有的接头形式和载荷状态,这样和不同接头形式以及载荷状态相关的等效结构应力就可以被明确地推导出来。结构应力K估值为通用的K估值提供了便利方法,下面将分别考虑两种情况:板边裂纹的K值求解和椭圆裂纹的K值求解。
1.板边裂纹形态下的K值求解
对于具有板厚为t、边缘裂纹深度为a、远端承受膜应力σtm和弯应力σtb的二维试样,在没有缺口效应的Ⅰ模式(张开型)的应力强度因子Kn,可以应用叠加原理求得,即:受膜应力时的应力强度因子Knm与受弯应力时的应力强度因子Knb之和:
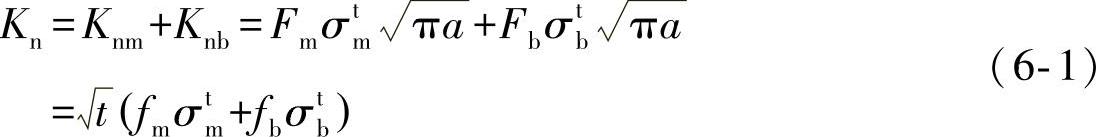
式(6-1)中的形状参fmfb,分别对应膜应力和弯曲应力情况下的形状参数,可通过权函数法求得,或直接查找应力强度因子手册[1]。
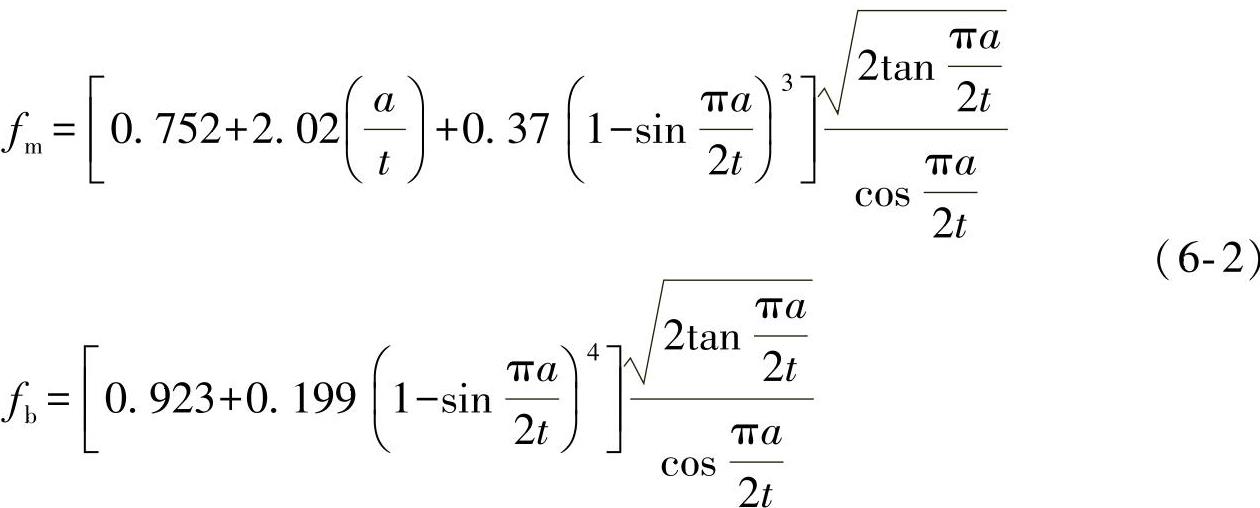
如先前所讨论,σtm和σtb表示远场的结构应力分量,认为与整个厚度t上的定义有关,如图6-2所示。一旦获得结构应力,应力强度因子就很容易从式(6-1)计算得到。
 (https://www.xing528.com)
(https://www.xing528.com)
图6-2 沿厚度方向自平衡的应力对小裂纹应力强度因子的影响
2.椭圆裂纹形态下的K值求解
一旦获得结构应力分量(σtm,σtb),相应的椭圆裂纹K值求解就可以通过和板边裂纹K值求解一样的方法建立。可参阅文献[2],与简单拉伸(σm0)和简单弯曲(σb0)类似,沿着厚度方向分布的结构应力有:
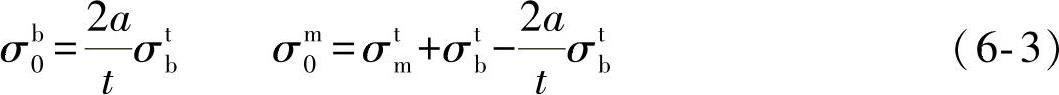
式(6-4)是文献[2]给出的椭圆裂纹应力强度因子K的解:
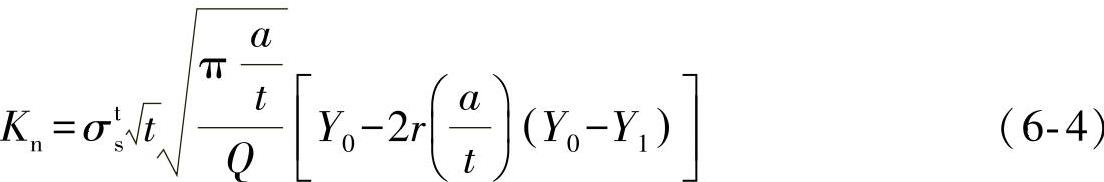
这里,σts=σtm+σtb,r=σtb/σts,空间参数Q、Y0和Y1可以从文献[2]中查到。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




