结构应力的力学解释与实验验证

基于有限元的基本理论，网格不敏感的结构应力法的力学解释并不困难。结构应力的计算基础是认为截面上节点力的合力一定与外力平衡，这样在划分有限元网格时，假如在给定外力的前提下划分20个网格的节点力的合力与这个外力平衡，那么划分10个节点力的合力也应与这个外力平衡。

图5-9a给出的是一个承受拉伸疲劳的搭接接头。图5-9b给出了壳单元离散模型（假定1/4对称），图中搭接焊缝通过一排倾斜单元来表示，焊脚等于板厚t。图5-9c给出了焊趾位置结构应力计算结果的归一化比较，其中壳单元类型不同：一个是4节点线性壳元，一个是8节点的二次壳元；网格大小也不同，它们的网格尺寸分别是0.5t、t、2t（t为板厚），但是比较以后可以看到，尽管单元尺寸与单元类型的积分阶次不同，焊趾上基于结构应力的应力集中因子却基本相同。

事实上，网格不敏感的原因完全可以从力的平衡角度去解释，因为在外力给定的情况下，同样一条焊趾或焊线上的节点力的个数无论多少，其合力都将与这个外力平衡，所以结构应力对有限元网格一定不敏感。当创建有限元模型时，注意在基于虚功原理将节点力转换为线力或线力矩时，要有足够的节点。

注意，结构应力的网格不敏感与通常的应力计算过程中为了提高计算精度而加密网格是完全不同的两个思考方向，在计算结构应力时追求过细的网格是没有必要的。结构应力对有限元网格不敏感这一特点在应用过程中有重要的价值，因为这将显著降低有限元网格数量，从而降低了对计算机硬件能力的要求，在硬件配置不是很高的计算机上，也可以完成较大规模的计算任务。

与名义应力、热点应力的概念相比，结构应力本身的物理意义更为明确，因为它是基于力的平衡这样一个物理概念推演而得到的，是具有整体一致性的应力。既然结构应力的物理意义明确，那么结构应力的存在是否可以用试验的手段进行验证呢？下面将要给出的结构应力测量方法可以回答这个问题^[2]。

如图5-10所示，结构应力定义中的膜力和弯曲分量可以通过同时在上表面和下表面使用一系列应变片的测试结果进行计算，例如A—A截面处的结构应力。如果两排应变片（B—B截面和C—C截面）被置于焊趾附近为线性应力分布区域，则截面B—B和C—C处的弯曲应力可以基于上下表面的测量结果计算得到：

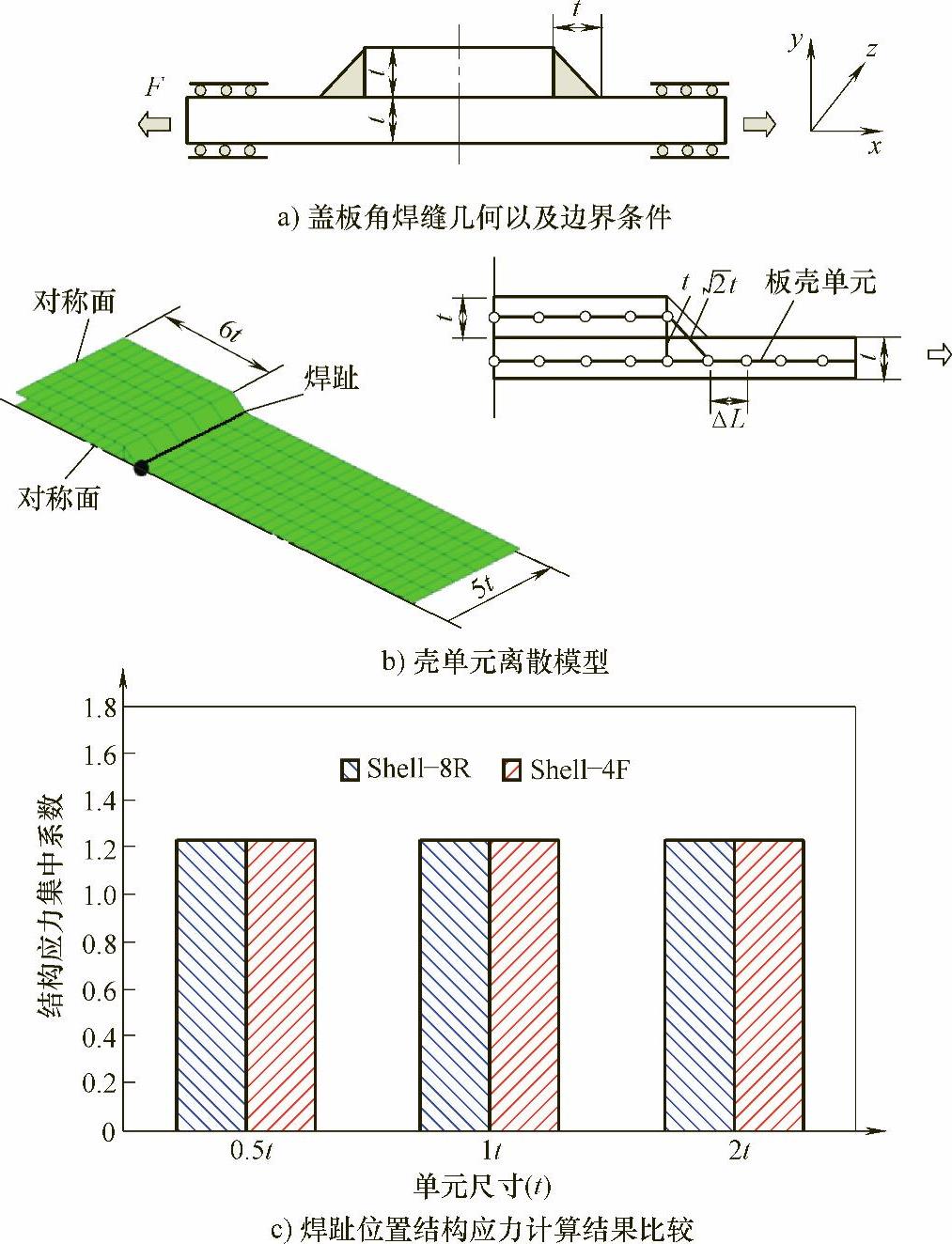
图5-9 结构应力的网格不敏感特性示意图

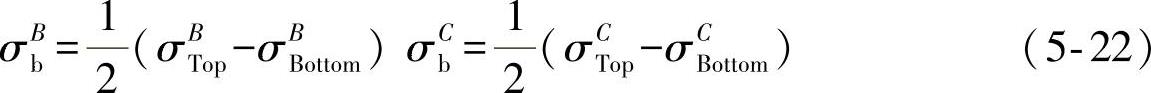
需要注意的是，如果截面B—B和C—C之间没有外载荷存在，则截面弯矩的变化可以表示为

式中 I——z方向单位长度的截面惯性矩。

注意到膜应力可以在测试中直接得到，这样在焊缝（A—A）处的结构应力就可以根据相应于B—B和C—C处的弯曲应力使用外推方法进行计算：(www.xing528.com)

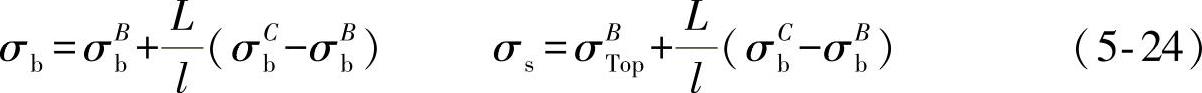
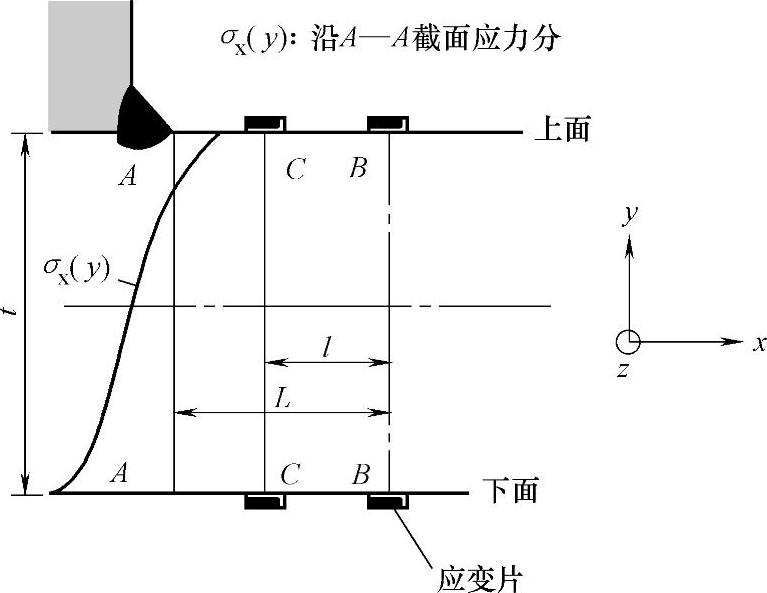
图5-10 结构应力测量

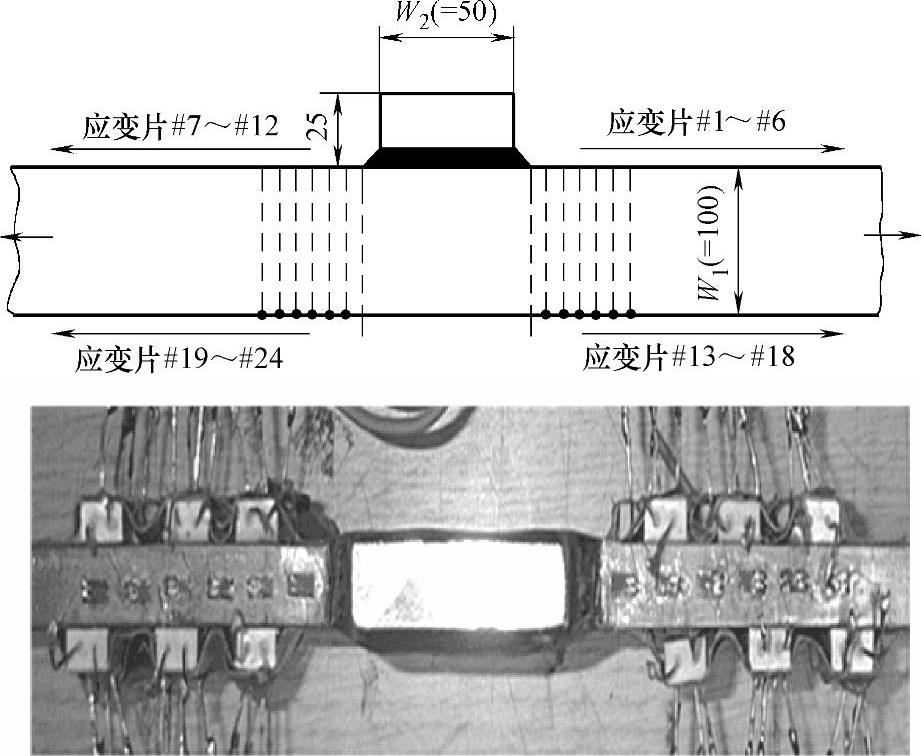
图5-11 结构应力测量试验

美国Battelle焊接研究所对结构应力进行了试验测试，对有限元计算的结构应力与试验测量的结果进行了对比。图5-11是一个典型的测试试件，图中给出了实际应变片的布置位置，图5-12～图5-13总结了对比结果[3-4]。

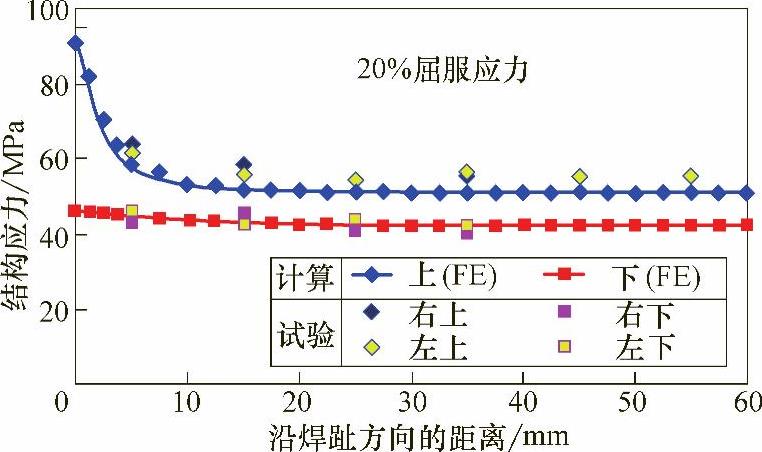
图5-12 20%屈服应力载荷情况下结构应力计算与试验对比

试验得到的结构应力的误差是由于试验手段的误差引起的，对于基于应变片的测量方法是可以接受的。为了降低误差的影响，使用位于试件左右两侧对称位置应变片的平均值，以确定焊趾位置结构应力，通过这样的处理，在20%屈服载荷和50%屈服载荷之间测量的结构应力结果基本一致，而且试验测量计算的结果和使用节点力计算的结果基本相同。

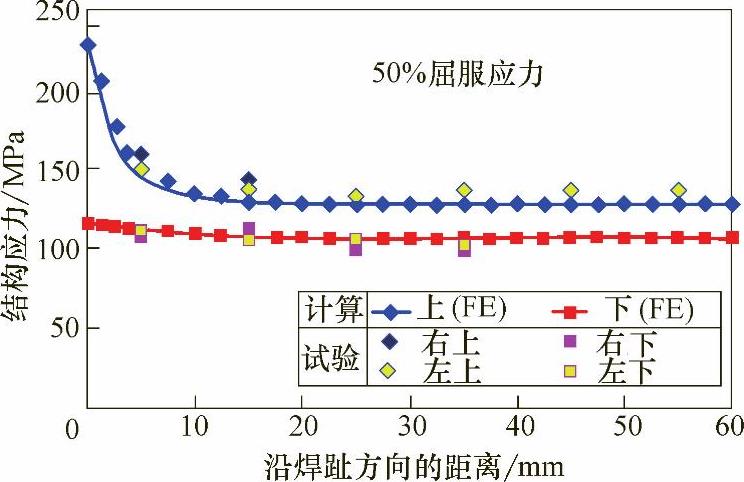
图5-13 50%屈服应力载荷情况下结构应力计算与试验对比