结构应力的定义与计算方法

图5-5a给出了外力作用下在焊缝截面上沿着厚度方向的应力分布，这个应力分布因含有缺口应力而呈现出高度非线性。虽然理论上或数值上直接求解这个非线性应力分布是很困难的，但是可以将这个高度非线性的应力进行分解^[2]。分解后，第一部分应力是只与外力相关，且与外力互相平衡的那一部分。

分解后，第二部分应力则是去掉了第一部分而余下的应力，被称为缺口应力。它虽然包含了非线性部分，但是由于第一部分已经与外力平衡，因此这部分应力的分布一定处于自平衡状态，图5-5b给出了分解为两部分应力的示意。

图5-5 截面内的应力分解示意

有了上述分析就可以定义第一部分为结构应力，第二部分为缺口应力，二者之和，就是原来截面上非线性应力的分布。这里忽略了剪切应力的影响，一个原因是它对焊缝开裂的贡献很小，如果剪切应力不能被忽略，那将是多轴疲劳问题，这里暂不讨论。

那么，为什么第一部分应力称为结构应力呢？因为它是满足平衡条件并可以用结构力学的方法计算得到。不失一般性，假设一个焊接接头的远场外力在截面上既有拉伸贡献的膜应力也有弯曲贡献的拉应力，参考图5-5，与外力平衡的是膜应力与弯曲应力之和。在给定板厚以后，截面内均匀分布的膜应力可以按照下式计算：

而截面内产生的弯曲应力可以按照下式计算：

由于已经定义的结构应力与外力平衡，因此结构应力即为膜应力与弯曲应力之和：

由式（5-13）可知，在计算结构应力时首先要计算线力f_y和线矩m_x，线力与线矩是指焊线（焊线是为计算需要而自行定义的线，该线可以定义在焊缝里，也可以定义在热影响区，由于焊趾是焊接结构的薄弱处，所以通常将焊线定义在焊趾上），单位长度上的力与力矩。在有限元计算时，单元边上的分布载荷要向节点转化，而结构应力法在利用节点力求线力和线矩时，却是这个过程的逆过程，还要将有限元求得的节点力和力矩转化为线力和线矩。

如图5-6所示，节点1和2在y轴方向的节点力及绕x轴的力矩分别为F_y1、F_y2和M_x1、M_x2；y轴方向单元边的线力及绕x轴的线力矩分别为f_y1、f_y2和m_x1、m_x2，根据力的平衡方程，可以求得式（5-14）。

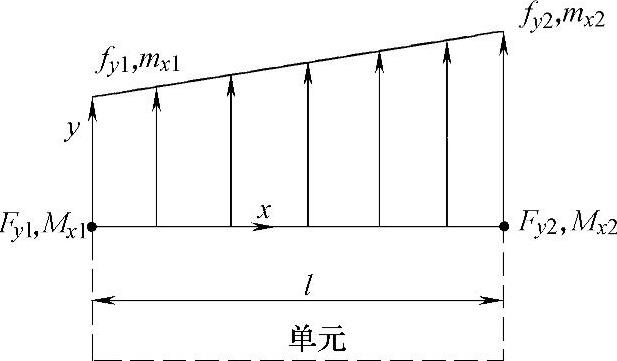
图5-6 两个节点时节点力及线力分布

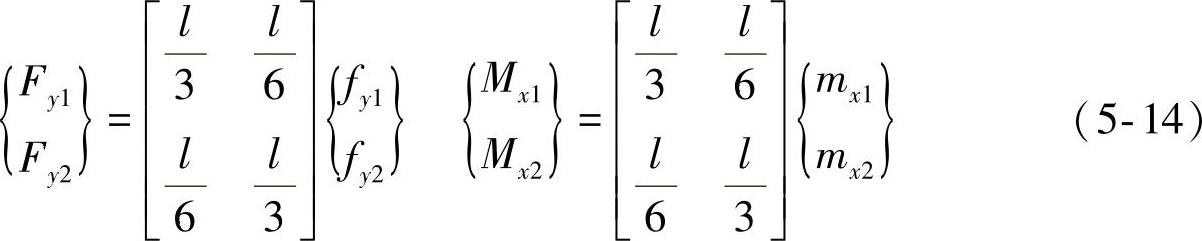
求式（5-14）右侧项矩阵的逆可得

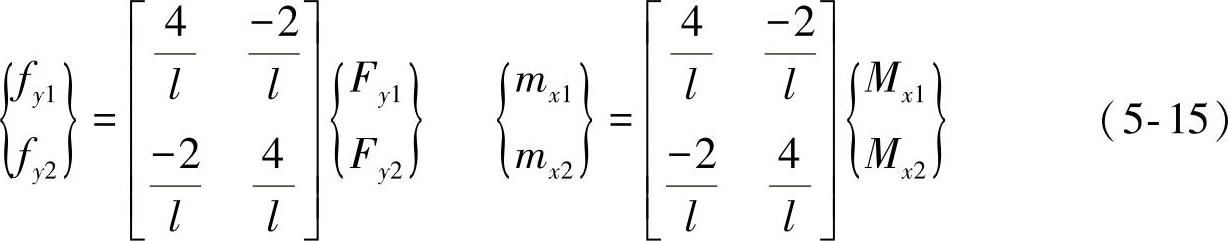
所以节点1及节点2的结构应力为

不失一般性，将一段焊缝划分成n个单元时，节点编号由1至n，焊线上的各节点距离为l₁至l_n-1，根据力的平衡方程，可求得各节点力F_yn与线力f_yn的对应关系。

(www.xing528.com)

式（5-17）中矩阵L只与节点距离相关，这里定义为单元长度等效矩阵：

为计算方便，下面给出了单元长度等效矩阵的逆矩阵L^-1的表达式：

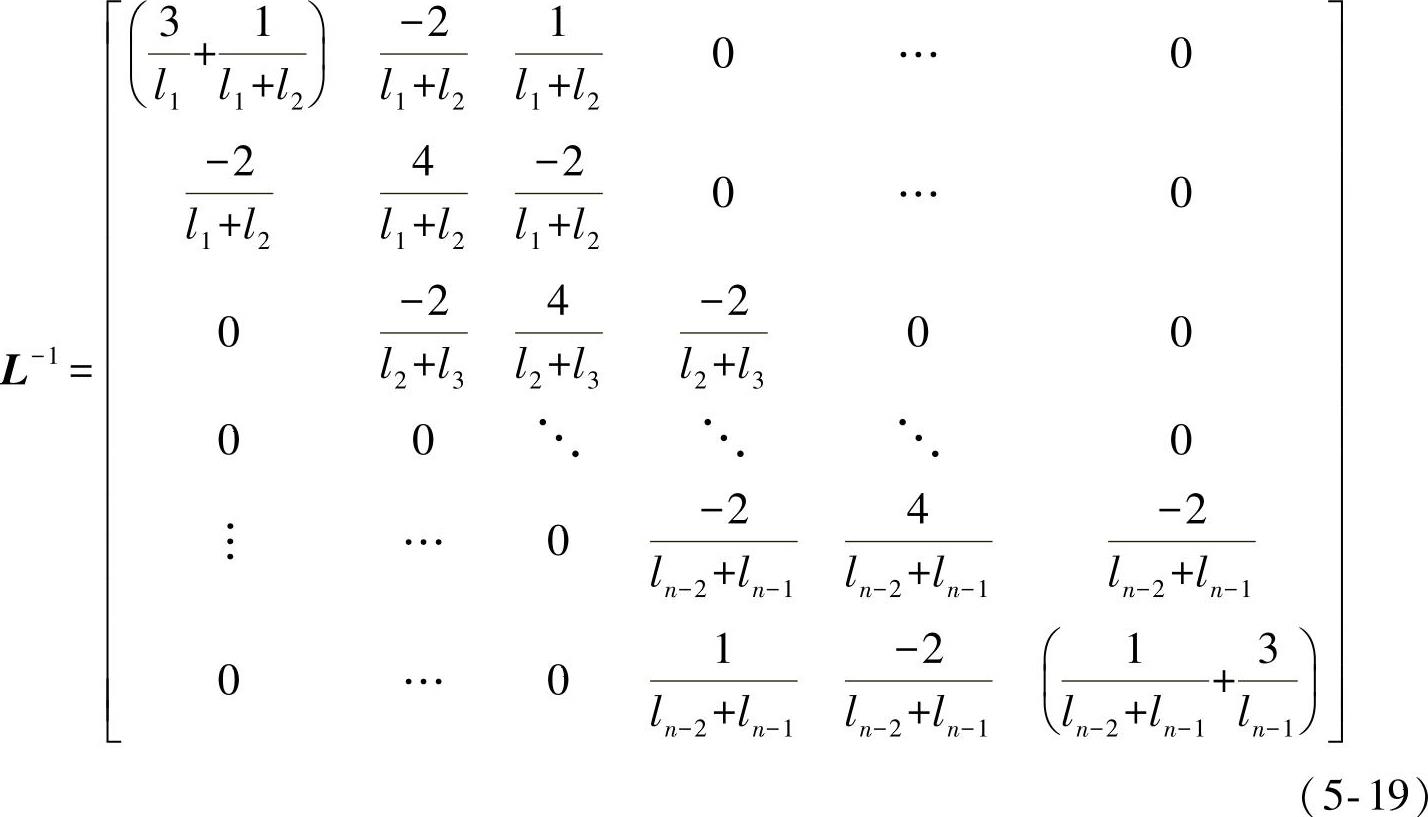
由此可得线力与节点力的对应关系：

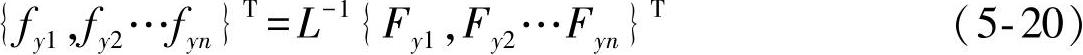
同理，线矩m_x与节点力矩M_x与上述表达式形式相同，这样当有n个节点在相同的单元厚度t的情况下，各节点的结构应力σ_n，以及各节点力F_yn和力矩M_xn可用矩阵方式表示为

式（5-21）即为结构应力计算公式，由上述分析及公式可见，结构应力有以下特征：

1）力学特征完全由外力模式与接头本身的板厚控制。

2）该公式是基于力的平衡概念而提出来的，且可以直接用结构力学公式计算。

3）在焊趾处，它给出了外力在焊趾上产生的应力集中。

4）在截面内，它给出了所在截面内沿着板厚方向的应力分布状态。

在利用有限元法计算结构应力时，要对给定的焊接结构创建有限元模型，这时最好采用板壳单元离散建模，当然也可以用三维块体单元离散建模，但是板的厚度方向至少要有两层以上的单元离散，且需要注意沿着板厚方向的节点要共线，因为只有这样才能如图5-7所示的那样将块体单元上的节点力顺利等效为板厚度中面上的力与弯矩。

然而不管用哪一种模型，在建模时均需要根据焊缝焊脚的实际位置定义焊线，即焊缝的焊趾与焊线对应。有焊缝建模和无焊缝建模的板壳模型中的焊线定义如图5-8所示。

图5-7 焊趾节点力和弯矩绕板中面在整个截面上力矩的形成

在采用板壳单元模型时，模型中可以建立焊缝对应的单元，也可以在模型中不考虑焊缝对应的单元。理论上，模型中不考虑焊缝单元的计算结果与考虑焊缝单元的计算结果相差很小，因为焊缝本身的单元对整体刚度的贡献很小。根据式（5-10）可以判断其对位移解的影响也将很小，而节点力的计算需要节点位移，因而对节点力的计算结果的影响也将很小。

基于力的平衡，可以将这些节点力等效为图5-7中等效的力与弯矩，然后利用式（5-21）可以得到线性系统下的结构应力的具体数值。

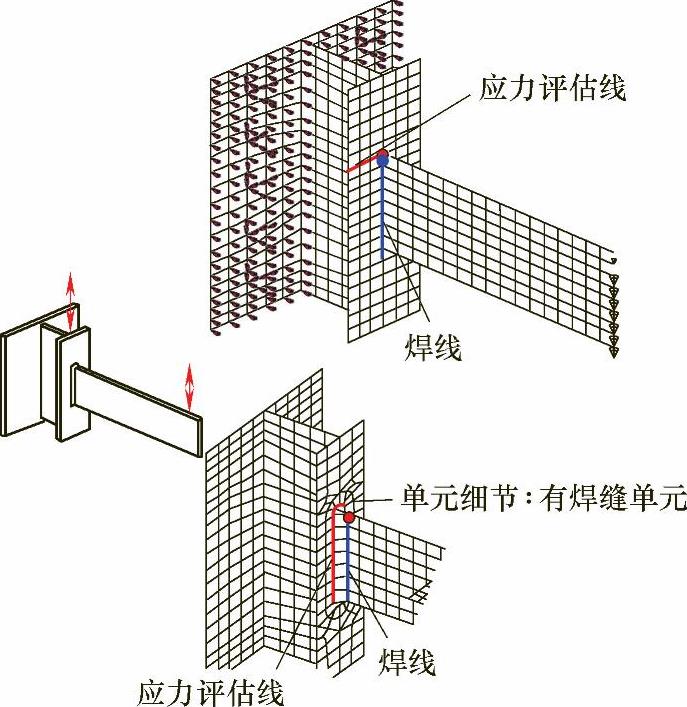
图5-8 有焊缝建模和无焊缝建模的板壳模型中焊线的定义