「从头学起」有限元方法：基础知识解析

考虑到本章即将引进的结构应力的计算过程中需要从有限元计算结果中提取节点力，也考虑到以后几章内容的需要，因此本节将简要介绍一些有限元的相关知识。

有限单元法（Finite Element Method，称FEM）是结构应力法的计算基础之一。有限元法的发展始于力学，但是其数学本质却是用数值法求解偏微分方程。因篇幅所限，这里只概括地介绍有限元法中与求解节点力相关的基础知识。

首先从一个简单的静力平衡的微分方程问题入手。设有一个承受均匀载荷的小变形悬臂梁，如图5-1所示。已知材料物理参数：杨氏模量E、梁截面几何形状、梁截面抗弯惯性矩I等。在均布载荷q（x）的作用下，根据材料力学知识就可以推导出它处于平衡状态下的变形微分方程。

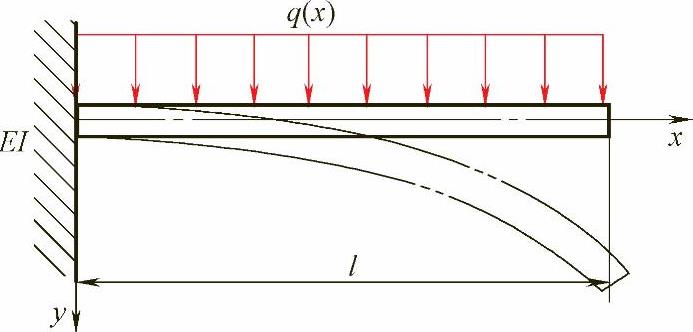
图5-1 承受均匀载荷的小变形悬臂梁

式中 y（x）——待求梁的变形曲线。

式（5-1）表明，所研究的梁的平衡状态等价于求解这个带有边界条件的微分方程。考虑到悬臂梁的具体边界条件，求解微分方程式（5-1）后，得到了它处于平衡状态下的变形表达式y（x）：

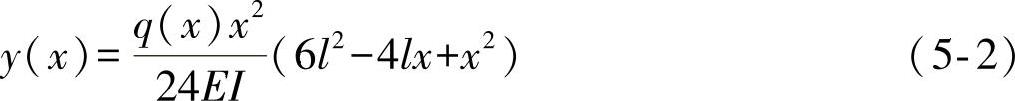
由式（5-2）很容易进一步求得梁内任意一点上的应变与应力。结构受力后处于平衡状态，可以用类似式（5-2）这样的微分方程来描写，但是求解这些微分方程时必须考虑相应的边界条件，而工程实际问题的复杂边界条件又很难用数学关系模型化，所以采用直接求解这些微分方程的方法会在工程上遇到一定困难，于是就出现了基于变分原理的有限元法。当前常用的商业有限元软件的基础算法是基于最小总位能原理，以位移为基本变量的位移有限元法。

在力学理论中最小总位能原理是这样定义的：在所有满足内部连续性和运动学边界条件的位移中，满足平衡方程的位移使得位能取驻值，如果驻值是极小值，则平衡是稳定的。简言之，如果受力系统处于稳定状态，那么该系统的总位能一定最小。这样当研究平衡状态时，最小总位能原理就可从能量的角度来设立另外一个求解途径，而这个途径与前面通过求解微分方程去研究平衡问题殊途同归。

为了解释能量原理，下面用图5-2所示的简单的受力弹簧系统给出能量原理的内涵^[1]。

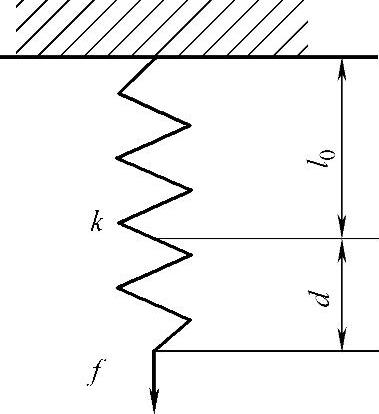
图5-2 一个受力弹簧系统

已知弹簧刚度系数为k，原长为l₀，下端施加垂向载荷f后，弹簧获得变形而处于稳定平衡状态。求解它的平衡状态，可以直接用力的平衡方程。下面不用力的平衡方程，而用最小总位能原理来求解由位移d度量的平衡状态，具体过程如下：

首先，假定位移为零的位置作为能量参考点，施加载荷后系统因获得变形而处于平衡状态。这时该系统的位能由两部分组成：第一部分是弹簧因拉伸变形而获得的位能，其大小为（kd²）/2；第二部分是载荷f因做功而损失的位能，其大小是fd，于是系统获得位移d后的平衡位置上系统的总位能是二者之和：

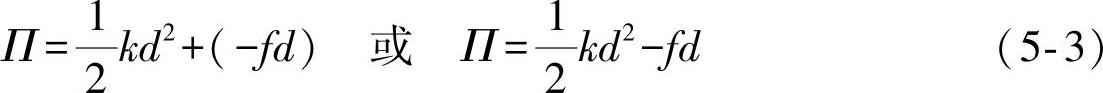
式中，第一项是弹簧获得的位能，第二项是载荷失去的位能。不难看出，系统总的位能Π是位移d的函数。

由最小总位能原理，真正的稳定平衡位置一定使总位能取极小值，即δΠ=0（式中δ为变分记号，类似于微分记号），所以对式（5-3）进行关于d的变分运算（类似于微分运算）得

（kd-f）δd=0 （5-4）

由于δd是不为零的任意小的假想虚位移，所以

kd-f=0 或 kd=f

即

d=f/k （5-5）

式中，d即为平衡位置，它与图5-3中系统总位能曲线的A点一致，该点为总位能最小点，即取极小值的那一点，也恰是描写系统处于平衡状态的点。

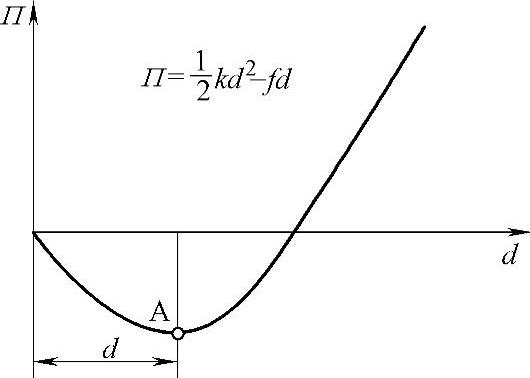
图5-3 系统总位能(www.xing528.com)

从这个简单的例子中可以看出：研究某个线性系统的平衡状态时，可以直接求解系统力的平衡方程，但也可以用最小总位能原理求解，二者虽然等价，但是内涵截然不同。

仍以图5-1所示的简单悬臂梁为例，该悬臂梁在均匀载荷作用下必然发生变形，且假设小变形条件下变形曲线为y（x），在图5-4中假设了几种可能的变形状态，但不论是哪一种满足边界条件的变形状态，总可以求出与之对应的总位能，即梁上载荷因变形而失去的位能与梁弯曲获得的应变能总和。

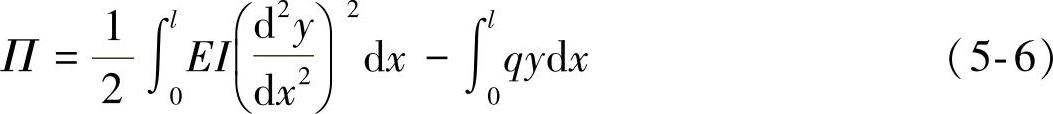
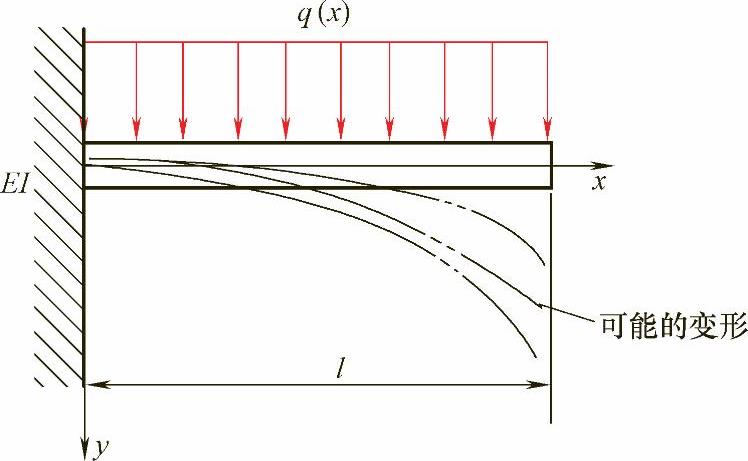
图5-4 寻找悬臂梁平衡状态

显然，总位能是关于变形曲线y（x）的函数（数学上称其为泛函，因为它是函数的函数）。不同的变形状态y（x）对应不同的总位能，那么哪个变形状态是真正的平衡状态下的变形状态呢？这个判断依据就是最小总位能原理，即：使能量取极小值的变形状态是真正的平衡状态。

由于工程上被研究对象的复杂性，人们可以将需要研究的对象人为地离散成有限多的小“单元”，在每个单元之间用若干个“节点”互相连接。在外力作用下，每个单元的节点将产生一定的位移，而在每个单元内部，任意一点的位移则可以由该单元节点上的位移按照某一种约定关系插值获得，这样在给定边界上的位移约束条件与外载荷F之后，每个单元都将获得类似于图5-2中小弹簧所获得的变形能量，对每个单元变形能求和，就可以获得结构离散后的总变形能，同时再考虑外力离开初始位置而失去的位能，那么系统获得的总位能就是：

式中Π_e——一个单元获得的能量；

m——单元总数；

D——离散后维数为n的自由度向量；

F——外载荷向量。

式（5-7）给出了系统的总能量，它从能量等价的角度实现了原力学模型的有限元模型替代。由于已经将结构的总位能表示为位移的函数，类似地对式（5-7）的每个自由度引入最小总位能原理，最后将得到满足平衡条件的一组方程：

可以证明结构总位能是位移的二次函数，运算式（5-8），将得到n个互相联立的关于位移的线性方程组，即式（5-9），式（5-9）可以简写为式（5-10）：

式中 k——单元刚度矩阵；

K——结构整体刚度矩阵，它是根据单元节点编号信息对每个单元累加而成的，其中每个k仅取决于构成单元的材料特性及几何形状。

根据几何形状及力学特点，许多商业有限元软件中定义了多种类型的单元，并存放在单元库里供建模时调用。

简言之，有限元法的力学特点是：①基于位移插值技术实现了有限个节点位移向单元内部任意一点位移的转换；②基于能量原理实现了微分方程向一组线性方程组的数学转换。许多文献都对有限元方法做了很好的介绍，如果读者有较好的力学基础，推荐阅读文献[1]。

清楚了有限元法的基本原理，就可以利用该方法获得结构应力所需的节点力，计算节点力的基本步骤如下：

1）引入位移约束条件求解式（5-10），首先得到的是全局位移解。

2）根据单元节点编号信息，从全局位移中提出单元上的节点位移。

3）将这些位移转换到单元的局部坐标系，然后与单元刚度矩阵相乘以后得到该单元的所有节点力。

在一些著名的商业有限元软件中，求解后的单元节点力已经被存储在结果文件之中，例如ANSYS软件的RST文件，提取单元节点力时用户只要清楚结果文件的存储格式即可。