费克第二定律求解非稳态传质问题

非稳态传质是指物质传递随时间变化而变化。例如，一片蔬菜受到热空气干燥时其中的水分传递、将糖果放入水中其中糖分子在固体到液体之间的传递等，这些都是瞬间非稳态传质的例子。

费克第二定律（Fick's Second Law）是在第一定律的基础上推导出来的，用于解决溶质浓度随时间变化的情况，即dc/dt≠0。

图7-3 物质传递过程示意图

如图7-3所示，将距离x处的扩散质浓度定义为C（x，t），通过A面的扩散通量为J（x）。费克第二定律指出，在非稳态扩散过程中，在距离x处，浓度随时间的变化率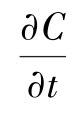等于该处的扩散通量随距离变化率的负值，即：

将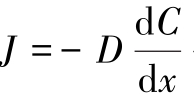代入上式，可以推出费克第二定律：

式中 C——扩散质的浓度，kg/m；

t——扩散时间，s；

x——扩散距离，m。

实际应用中，食品中溶质分子的扩散系数D都是随浓度变化的，但为了简化扩散方程，往往将D近似为恒量进行处理，再结合初始条件和边界条件求出方程的解，利用通解可以解决非稳态传质的具体问题。下面介绍利用费克第二定律分别求解在半无限长介质、无限长介质和有限长介质中的非稳态扩散情况。

所谓半无限长介质，是以x=0平面为边界，在x的正方向可以无限延展的物体。尺寸无限大的物体只存在于理论中，它所表示的实际意义为：分子在极长的物体内传质或者传质时间非常短时，即可将该物体视为半无限大物体。如图7-4所示，相B为半无限长介质，扩散质在相A中的浓度为C_s，其数值不随时间发生改变。

图7-4 半无限长介质中的扩散过程

对于此类物体的求解，首先应确定初始条件及边界条件。

初始条件：

C（x，t=0）=C₀

t=0时，相B中各处粒子浓度为C₀。

边界条件：

C（x=0）=C_sC（x=+∞）=C₀

在相A和相B的界面处（x=0），扩散质的浓度始终为C_s；在介质的无穷远处（x=+∞），扩散质的浓度为C₀。

结合费克第二定律，可得到该问题的通解为：

式中 C_x——扩散质在半无限长介质内距表层x时的浓度，kg/m³；

C₀——扩散质在半无限长介质中的初始浓度，kg/m³；

C_s——扩散质在半无限长介质外的表层浓度，kg/m³；

D——扩散质在半无限长介质中的扩散系数，m²/s；

t——扩散时间，s；

x——扩散距离，m。

注：erf（error function）为误差函数，自变量x的误差函数定义为：

图7-5所示为随时间推移，扩散质在半无限长介质中的浓度分布情况。

当物体的总浓度和密度恒定时，式（7-25）可以进一步表示为：

图7-5 不同时间下扩散质在半无限长介质中的浓度分布（t₂＞t₁）

式中 w_x——扩散质在半无限长介质内距表层x时的质量分数，%；

w₀——扩散质在半无限长介质中的初始质量分数，%；

w_s——扩散质在半无限长介质外的表层质量分数，%。

[例7-3] 塑料包装中双酚A在食品中的渗透。

双酚A型环氧树脂和双酚A型聚碳酸酯等材料，从20世纪60年代以来就被用于制造塑料（乳）瓶以及饮料罐内测涂层等，是常见的食品包装材料。研究人员通过动物实验发现，双酚A可能会增加女性患乳腺癌的危险。当一个装满牛乳的牛乳瓶在沸水浴中加热时，已知双酚A在100℃时在牛乳中的扩散系数为D=4.6×10^-10m²/s，包装盖中双酚A的质量分数w_s=1.2%。问：需要经过多长时间距离塑料瓶盖x=0.1mm处牛乳中双酚A的质量分数能够达到0.1%。

解：由题意可知，双酚A只渗漏到牛乳表面非常薄的地方，因此可将牛乳视为半无限大物体。

根据半无限大物体内分子扩散的通解，即式（7-26）：

求解erf反函数，即逆误差函数：

即：

无限长介质可以看作是两个半无限长介质相A和相B的连接，连接处界面表示为x=0。扩散质在相A和相B中的初始浓度分别为C₂和C₁，假定C₂>C₁，则扩散质由相A向相B发生扩散。在极短时间内，任何扩散过程都可以看作是发生在无限长介质中（图7-6）。

图7-6 无限长介质中的扩散过程

对于此类问题求解，首先应确定初始条件和边界条件。

初始条件：

C（x <0，t=0）=C₂C（x >0，t=0）=C₁

t=0时，相A中各处粒子浓度为C₂，相B中各处粒子浓度为C₁。

边界条件：

C（x=-∞）=C₂C（x=+∞）=C₁

随时间推移，在相A和相B的无限长边界处扩散质的浓度始终不变，分别保持为C₂和C₁。浓度变化趋势如图7-7所示。

图7-7 不同时间下扩散质在无限长介质中的浓度分布（t₂＞t₁）

结合费克第二定律，可得到该问题的通解为：

式中 C_x——扩散质距相A与相B界面处x时的浓度，kg/m³；

C₁——扩散质在相A中的初始浓度，kg/m³；

C₂——扩散质在相B中的初始浓度，kg/m³；

D——扩散质在无限长介质中的扩散系数，m²/s；

t——扩散时间，s；

x——扩散距离，m。

物质在有限长介质中扩散时，如图7-8所示，相B为有限长介质，为计算方便，将x的零点设置在扩散远端，在相A和相B的界面处，x=L，L为介质的长度。

该类问题的初始条件为：

C（x，t=0）=C₀(www.xing528.com)

t=0时，相B中各处粒子浓度为C₀。

图7-8 有限长介质中的扩散过程

边界条件为：

在相A和相B的界面x=L处，扩散质的浓度始终为C_s，在x=0处，扩散质随x的变化率为0，如图7-9所示。

图7-9 不同时间下扩散质在有限长介质中的浓度分布（t₂＞t₁）

结合费克第二定律，可得到该类问题的通解为：

式中 C_x——扩散质距扩散远端界面处x时的浓度，kg/m³；

C₀——扩散质在有限长介质中的初始浓度，kg/m³；

C_s——扩散质在相A和相B界面处的浓度，kg/m³；

D——扩散质在有限长介质中的扩散系数，m²/s；

2L——有限长介质的长度，m；

t——扩散时间，s；

x——扩散距离，m。

当相B中扩散质浓度高于相A时，扩散质由相B向相A扩散，式（7-28a）可变为：

当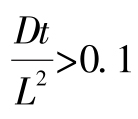时，式（7-28b）中的前三项（即n=0，1，2）足以进行系列收敛。对式（7-28b）两边进行求导可得：

式（7-29a）表明，当D为常数，则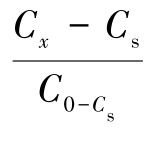与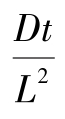的半对数图是线性的，扩散系数D可通过斜率进行计算。

表7-3 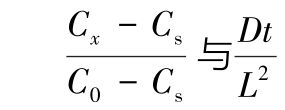的函数对应值

也可利用海斯勒图（Heisler Chart）进行求解，如图7-10所示。

图7-10 非稳态扩散浓度分布

有限长介质中的非稳态扩散过程是实际应用中最为常见的情况，其求解过程也最为复杂，需要结合复变函数及数学分析等方法共同解决。如腌制是常见的食品加工技术，食品中存在水分故在腌制过程中会产生渗透压，导致传质现象的发生。在渗透压的影响下，溶质会扩散进入组织，而水分子会渗透出来，最终形成腌制品。我们也可以用有限平板公式来模拟腌制过程中的盐分（或其他组分）在不同介质中的传递过程，探究在不同时间、不同部位的盐分渗透情况或含盐率，计算得出有效扩散系数。

[例7-4] 苹果片中水分的扩散。

10mm厚的苹果片中含有30%的水分，强制对流条件下可以保持苹果表面的水分与空气中水分含量保持平衡，空气中含水量为5%。水分的扩散系数为1×10^-9m²/s。计算苹果片中心水分干燥至10%所需的时间。

假定：水分从苹果片扩散到空气中的过程为一维扩散，水分扩散过程中不受阻力影响，苹果无收缩。

解：根据题意可得：

代入图7-10中，可找到：

求得：

t=0.52×0.01²×10⁹=52000（s）≈14.4（h）

[例7-5] 鹰嘴豆浸泡时的传质过程（Rui Costa，2018）。

鹰嘴豆最常见的食用方法是在浸泡后进行烹调，其浸泡过程中所发生的传质现象与浸泡时的水温密切相关，在常温水中浸泡时发生的基本是水分转移的变化；在高温水中浸泡时除了水分转移，还会发生淀粉凝胶化（温度55℃以上）等现象。对鹰嘴豆浸泡时的传质过程进行探究，建立传质数学建模，有利于进一步优化鹰嘴豆浸泡过程，实现最大产量和最小能耗。本例研究了鹰嘴豆浸泡过程中的水分传递、淀粉糊化等动力学过程。

鹰嘴豆的种皮—子叶之间有一定孔隙（图7-11），这些孔隙可以用来解释初始的水吸收。在浸泡时，吸水是由种皮吸收开始，然后扩散到子叶。在到达子叶表面后，水进一步进入鹰嘴豆并占据更多的自由空间，如开放的毛细管和胶束间空间，并被淀粉、蛋白质和纤维吸收。随着吸收的发生，分子的重排将导致肿胀即鹰嘴豆体积增大。同时，吸水提供的溶剂可以溶解固体和介质，导致可溶性固体损失。这些现象将一直持续到鹰嘴豆内部和外部溶液的浓度达到动态平衡。根据费克第二定律[式（7-24）]对吸水和固相损失进行建模。在传质模型中，将鹰嘴豆看作球形，平均半径为5mm。在浸泡过程中，假设鹰嘴豆表面的恒定特性，在没有外部阻力的情况下进行建模，对实验数据进行拟合，得到如下数学关系式：

式中 M——鹰嘴豆在浸泡一段时间后的水分含量（M_w）或固体含量（M_s），kg；

M_∞——鹰嘴豆在浸泡无限延长时的水分含量或固体含量，kg；

M_i——鹰嘴豆在浸泡中某时刻的水分含量或固体含量，kg；

D——扩散系数，m²/s；

r——种皮半径，m；

t——鹰嘴豆浸泡时间，s。

图7-11 鹰嘴豆种皮—子叶示意图

将鹰嘴豆浸在水里后，在第一分钟水分含量快速增加（图7-12）。水吸收的驱动力在浸泡过程中随着时间的延长而减小，最终达到零，这里认为水吸收的驱动力是无限时间后的平衡水含量M_∞和各时间点水含量M的差。在较高的温度下，淀粉和蛋白质开始吸收水分，所以最大含水量C_w，∞随温度的升高而增加。在25~100℃温度变化范围内，水扩散系数介于1.12×10^-10~3.83×10^-10m²/s。25~50℃以及75~100℃范围内可以观察到扩散系数明显增加。然而，在50~75℃范围内没有发现这种现象。这主要因为在该温度范围内，会发生糊化现象，即水与淀粉相结合。与淀粉结合的水无法进一步扩散到鹰嘴豆的核心，整体上减缓了水的扩散。另一方面，高温会导致水黏度降低，自扩散系数增大，因此水的扩散系数随着温度的升高而增加。当我们比较50℃（略低于糊化温度）和75℃（已经高于糊化温度）下得到的值时，这两种现象的净效应导致水的扩散率略有增加，但并不显著（表7-4）。除了原料的可变性外，由于扩散率与半径的平方成正比，所以扩散率的差异也受到所选择半径的影响。

图7-12 25、50、75和100℃时鹰嘴豆质量M_w随时间变化的实测数据与预测范围

表7-4 鹰嘴豆中水分扩散系数及固体（溶解）扩散系数

注：σ——样本的标准差，其单位与样本的单位相同；

σ（D）——相对标准偏差，由标准偏差除以相应的平均值乘100%所得，%；

C_w，∞——无限时间中单位物体中的含水量，g/100g；

f_s，∞——无限时间中固体颗粒在浸泡过程中损失的比例，g/100g；

d.b.——干基（Dry Basis），以单位质量无水固体为基准表示湿固体中的水分；

RMSE——均方根误差。

将鹰嘴豆浸泡过程中的传质变化分为三个周期。第一传质期的特征是密度的增加，到达这个点所需要的时间随温度升高而减少，密度增加与质量增加相对应。第二传质期对应于实现5%固体损失所需的时间，该周期的持续时间与固体扩散率成反比。在25~50℃以及75~100℃范围内可以观察到固体损失，但50~75℃范围内，因为此范围内发生的胶凝作用减缓了固体损失。在此过程中，水和固体的扩散转移与体积增大引起的流体流动同时发生。第三传质期发生在固体损失达到5%之后直至浸泡结束。其原因与上述类似，主要由于低于糊化温度下的固体损失，以及高于糊化温度时的吸水。

[例7-6] 白蘑菇菌盖渗透脱水时的传质过程（J.E.González-Pérez，2019）。

对白蘑菇菌盖渗透脱水时的传质过程进行探究。渗透脱水（Osmotic Dehydration，OD）是一种固液接触的部分脱水方法，将食品浸入高渗溶液中进行脱水，同时食品也可以从溶液中吸收溶质，其作为干燥的预处理可改善食品的最终特性。白蘑菇（双孢蘑菇）可以用NaCl水溶液渗透脱水来延长其保质期。将白蘑菇菌盖塑造成半球壳形状，使用非稳态2D扩散模型对水分损失和溶质富集进行建模，评估白蘑菇渗透脱水过程中传质情况，估算扩散期间扩散系数，并统计在不同浓度NaCl水溶液中脱水时水分流失随时间的变化。

图7-13是确定产品变形的图像所使用的分析步骤：首先拍摄原始图像，然后制作三个颜色簇的简化图像，再去除非产品颜色簇，形成灰度图像，最终描绘出产品轮廓（图像对应于在40℃，10% NaCl水溶液中处理180min的样品）。

图7-14是菌盖轮廓处理过程：将图7-13（1）中原始图像进行简化处理得到图7-13（4）。图7-14（1）中为多个经过简化处理的菌盖轮廓，对齐后得到图7-14（2），将图7-14（2）中图形进行平均后形成轮廓图7-14（3）（图像对应在40°C、10%NaCl溶液中处理5min的样品）。

图7-13 菌盖图像处理过程

图7-14 菌盖轮廓处理过程

图7-15表示菌盖分别在10%和25%NaCl水溶液中，当温度分别为40、60、80℃时水分随时间的流失程度[（1）和（2）]及溶质随时间的增加程度[（3）和（4）]。其中，点表示实验中所测得的数据，实线表示考虑脱水收缩的模型拟合，虚线表示未考虑收缩的模型拟合。在此模型中主要考虑两个传质过程，一个是水分从菌盖内部向外扩散的过程；另一个是溶质从溶剂中向菌盖内部扩散的过程。当模型考虑菌盖收缩时，水的扩散系数在1.1×10^-9~4.6×10^-9m²/s范围内，溶质扩散系数在1.1×10^-9~1.8×10^-9m²/s之间。在渗透脱水过程中升高温度会增加产品中的水和溶质迁移率（P<0.05）。温度和渗透浓度对传质速率没有显示出显著影响（P>0.05）。

图7-15 不同情况下白蘑菇菌盖的水分流失及溶质获得示意图

—〇—T=40℃ —□—T=60℃ —△—T=80℃