分子扩散只有在固体、静止或层流流动的流体内才会单独发生。在湍流流体中，由于存在大大小小的旋涡运动，而引起各部位流体间的剧烈混合。在流动着的流体中，不同浓度的质点依靠宏观运动相对碰撞混合导致浓度趋向于均匀地传质过程称为湍流扩散。显然，在湍流流体中，虽然有强烈的涡流扩散，分子扩散也是时刻存在的，但涡流扩散的通量远大于分子扩散的通量，一般可忽略分子扩散的影响。
对涡流扩散，其扩散通量的表达式为将上述式（7-5）中扩散系数D替换为涡流扩散系数De。其中，分子扩散系数D是物质的物理性质，它仅与温度、压强及组成等因素有关。而涡流扩散系数De与涡流黏度一样，与流体的性质无关，而与湍流的强度、流道中的位置、壁面粗糙度等因素有关，因此涡流扩散系数较难确定。
在一个系统中，传质过程几乎总是与介质的整体运动同时发生。对流一般可以分为自然对流和强制对流。自然对流是由于热量或质量传递本身引起的，而强制对流是由独立于传递的因素引起的。
对流传质是指壁面与运动流体之间，或两个有限互溶的运动流体之间的质量传递。传质单元操作多发生在流体湍流的情况下，此时的对流传质就是湍流主体与相界面之间的涡流扩散与分子扩散两种传质作用的总和。
描述对流传质的基本方程与描述对流传热的基本方程及牛顿冷却定律类似，可采用下式表述：
式中 NA——对流传质的通量，kg/（m2·s）；
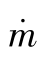——质量流率，kg/s；
ΔCA——组分A在界面处的浓度与流体主体浓度之差，kg/m3；
km——对流传质系数，m/s；
A——对流传质界面面积，m2。
在传质计算中可将变量无因次化，得出如下无因次数群：
例如，当气体或液体在降膜式吸收器内做湍流流动，Re>2100，Sc=0.6~3000时，实验获得的结果为：
Sh=0.023Re0.83Sc1/3，与圆管内对流给热的关联式Nu=0.023Re0.83Pr0.3~0.4相比较，不难看出传热与传质之间的类似性。
[例7-2] 不同食物在油炸时的传质过程（Afsaneh Safari，2018）。
油炸是食品加工的主要方法之一，在加工过程中热量和质量的传递是同时进行的。对流传热系数h和传质系数km直接影响油炸食品的质量和安全，因此在优化和控制过程中得到了广泛的关注。在油炸时，由于油的高温，产品在浸入后表面水分立即开始蒸发，由此产生的水分梯度导致水通过扩散从食品中心转移到表面。随后，油由食品表面向食品内部扩散。对流转移水分的速率很大程度上取决于传质系数km。
根据传热系数与传质系数的类比可知，随着时间的推移，两曲线的变化趋势相同，各影响传热系数的因素也会影响传质系数。因此，随着水分流失和由此产生的湍流，传质系数增加到最大值。然后，由于水分梯度随着时间的推移而减小，从而导致传质系数的降低，在过程结束时呈现下降趋势。在此基础上，提出了一些相关系数的关系式。例如，路易斯（Lewis）关系的正相关表述如下：
式中 h——传热系数，W/（m2·K）；
ρo——油的密度，kg/m3；
CPo——油的比热容，J/（kg·K）。
在该案例中，传质系数km随传热系数h的增大而增大。然而，有些油炸过程中传热系数和传质系数的趋势是不同的，传热系数呈现出急剧上升的趋势，而传质系数则是逐渐上升的，并且在不同的时间达到了最大值。但是，可以建立两系数最大值之间的相关性：
km（max）=- 8×10-11h2max+1×10-7hmax- 5×10-5R2=0.83
最大传热系数（Maximum Heat Transfer Coefficient，hmax）也与同时间相应的传质系数[Corresponding Mass Transfer Coefficient，km（corr.）]有关。
km（corr.）=- 9×10-11h2max+2×10-7hmax- 6×10-5R2=0.91
这些相关性已经建立，并可用于水分活度Aw=0.45~0.75、温度为20~180℃的甘薯及类似产品的油炸过程。
研究还发现，油炸传质系数还会受到温度及食物中不同组分添加量的影响。两种米果制作的温度范围为150~190℃，当温度升高时，传质系数随温度升高呈线性增加。此外，添加鱼粉的米果传质系数较低。
不同食物在油炸过程中的传质系数不同，如表7-1所示，将芋头、南瓜、番薯处理成相同的圆柱形并进行油炸，结果显示番薯的传质系数最高，其次是南瓜和芋头。这表明不同的食品基质和成分会对传质系数产生影响。
表7-1 部分食品油炸过程中传质系数
食品加工厂在180℃下油炸南瓜，已知此时的质量流率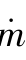
为0.5kg/s，对流传质界面面积为2m2。根据表7-1给出的数据，求此时南瓜在界面处的浓度与油中浓度之差及传质通量。(www.xing528.com)
解：根据式（7-12）得：
工程文献中充满了有关材料性能和操作条件传递系数的经验性或半经验性数据，这些数据一般以图形、图表或相关方程的形式出现。这里将讨论一些常用的相关经验式（表7-2）。
表7-2 对流传质常用的经验关联式
续表
注：契尔顿（Chilton）和柯尔本（Colbum）采用实验方法关联了对流传热系数与范宁摩擦因数（Fanning Friction Factor）、对流传质系数与范宁摩擦因数之间的关系，得到了以实验为基础的类比关系式，称为柯尔本类似律（Colbum Analogy）或J因数类比法。其中，jD为柯尔本传质因数，jH为柯尔本传热因数。
①爬流是指来流速度很小，流速缓慢，颗粒迎流面与背流面流线对称。
②空塔流速是指在精馏、吸收等操作中所应用的板式塔或填料塔，在计算通过塔内的流体速度时，不考虑塔内装入的物件，按空塔计算流体通过塔的平均流速，以流体的流量被塔的总截面积除而得到的数值。此处指流化床的空塔流速。
在众多过程中，物质间的质量传递是至关重要的。例如，干燥过程是以水分子从液体或湿物质转移到气体（通常是空气）为基础的；果汁的除氧过程是使氧气从在液体中溶解的状态到气体的过程；液—液萃取过程是溶质从一种液体溶剂向另一种液体溶剂的转移。
路易斯（Lewis）和惠特曼（Whitman）在1924年提出了双膜理论（Double-Film Theory）。该模型假设存在两个停滞或层流膜，每个都在两相之间边界的一侧。这两相可以是气体和液体，也可以是两种不混溶的液体，物质通过浓度或者分压的差异从一个相转移到另一个相（严格地说，这种转移是由于对介质亲和力不同而造成的，只有在理想混合物情况下，才能用浓度的差异取代物质对亲和力的差异）。
双膜模型把气液间的对流传质过程描述成图7-2的形式，可以作如下假设：
（1）模型假设存在两个停滞或层流膜，每个都在两相之间边界的一侧。
（2）在气液相界面处，气液两相处于平衡状态。
（3）在两个停滞或层流膜以外的气液两相主体中，由于流体的强烈湍动，各处的浓度保持一致。
图7-2 双膜模型表示的两个接触相的浓度或分压分布图
考虑图7-2气液接触情况，假设A物质从气体运输到液体，由于在界面上不存在累积，所以A从气体到界面的通量必须等于从界面到液体的通量：
式中 kG——气膜对流传质系数，kg/（m2·s·Pa）；
kL——液膜对流传质系数，m/s；
pA，G、pA，i——物质A在气体中和界面的分压，Pa；
CA，i、CA，L——分别是物质A在界面和液体中的浓度，kg/m3。
由于界面的平衡，CA，i和pA，i通过相应的平衡函数相互关联。例如，如果假设符合亨利定律，则相互关系为
式中 s——物质A在液相中的溶解度系数，kg/（m3·Pa）。
我们定义了以液相浓度差为驱动力的总传质系数（Overall Mass Transfer Coefficient，KL，m/s）：
同样，我们可以定义以气相总压差来表示驱动力的总传质系数[KG，kg/（m2·s·Pa）]：
总传质阻力（Overall Mass Transfer Frication）等于液膜和气膜两个单独阻力之和：
通常情况下，一侧阻力比另一侧阻力大得多，例如，假设气体中A的阻力比液体中要小得多，即kG≫kL，则在这个例子中：
以上所建立的方程，仅在液体—气体服从亨利定律的情况下有效，否则必须用更精确的平衡函数或吸附等温线等实验数据进行表征。
在食品加工过程中，物质传递过程都会随着时间的变化而变化，所以稳态传质在实际食品加工过程中是很难实现的，但其可作为一种理想状态模拟加工过程中的某些时间点。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
