如何优化食品工业中的非稳态传热过程？

食品工业中的许多过程，如罐头食品的热灭菌和食品速冻等，都属于非稳态热传递过程。非稳态导热过程中在热量传递方向上不同位置处的导热量处处不同，这是由于内能随时间发生了变化，是区别于稳态导热的一个特点。

以平板上的瞬时传热为例（图5-2）。假设热流在垂直于板表面的方向上单向传递。考虑与表面距离为z处的一切面，设切面厚度为d_z。

图5-2 平板上的非稳态传热

非稳态时，热吸收速率（q_i）与热释放速率（q_o）不相等，二者的差值是热积累q_a（数值可正可负）。如果平板上无热量产生，热平衡方程如下：

热传导时：

热积累速率与温度变化率有关，计算如下：

假设整个切片的特征常数k、C_P和ρ保持不变。代入热平衡方程中，消除所有S并结合热扩散系数α的定义，可得：

通过分析三维体积微元的热吸收和释放，将以上等式拓展应用至三维传热，可得：

式中 q_i——热吸收速率，W；

q_o——热释放速率，W；

q_a——热积累，W。

需要注意的是，如果材料不是各向同性的，则热扩散系数可能在x、y和z方向上有所不同。

式（5-26）被称为傅立叶第二定律（Fourier's Second Law），可反映温度分布和热流量分布随时间空间的变化规律。方程表示了固体内温度随时间的变化规律，其解析解适用于常规几何体（平板、球体、圆柱体）和简化的边界条件。针对更复杂的情况，必须使用数值法。

以厚度为2L的无限平板为例。假设平板各处的初始温度为T₀，两表面与温度恒为T_∞的流体瞬间接触。在时间t时，平板内温度T分布是如何？

首先，将变量转换为无量纲表达式。无量纲温度表达式θ可定义为：

式中 θ——无量纲温度；

t——时间，s；

T_∞——流体的恒定温度，K；

T——平板在时间t时的温度，K；

T₀——平板各处的初始温度，K。

物理意义上，θ表示实际温差与t=t_∞时理论温差的比值。

接着，我们定义表面阻力和内部传热阻力之间关系的无量纲表达式。设h是从流体到板面的对流传热系数，k是固体的导热系数。Biot数（一个无量纲数）定义为：

确定一个与平板中心面距离为z的原点，定义一个无量纲距离参数z′如下：

时间t的无量纲参数Fourier（F₀）的定义如下：

式中 N_Bi——无量纲Biot数；

z——确定原点与平板中心面的距离，m；

z′——无量纲距离参数，m；

F₀——时间t的无量纲参数；

α——热扩散系数，m²/s；

L——无限平板（厚度为2L）的1/2，m；

h——对流传热系数，W/（m²·K）；

k——导热系数，W/（m·K）。

就无量纲数群而言，傅立叶第二定律方程的一般解适用于以上所给的无穷大系列的边界条件：

参数β_i与Biot数的关系如下：

如果时间足够长（如F₀>0.1），则总和近似收敛于第一项。此外，如果表面热阻相比于内阻可忽略不计（N_Bi=∞，因此β=π/2），则解析式可变换为：

实际上，N_Bi=∞的假设在许多情况下是合理的。例如，蒸汽加热固态罐头食物，湍流空气加热或冷却的大块固体食物等。

式（5-34）表示了平板中温度的分布情况。温度是位置参数z′和时间参数F₀的函数，其中位置函数是三角函数，时间函数是指数函数。

在平板中的指定位置z′，时间—温度关系可由以下一般形式的等式近似表示：

式中 lnj——lnθ关于t的直线在y轴上的截距。

图5-3 非稳态传热的一般形式图

令z=0，可求出平板中心轴的温度T_c。

对厚度为L的平板，若仅从一面上交换热量，则可视其为厚度为2L，可双面进行热交换的平板。

对于其他几何形状（无限圆柱体、球体），可得到类似的一般形式方程。如果时间足够长，这些方程都可以表示为lnθ与t之间的近似直线（图5-3）。可从文献中查阅不同形状几何体对应不同N_Bi值的温度分布图表（Carslaw H S、Jaeger J C、Feshbach H，1986）。如图5-4~图5-6为此类图表的一般形式。

图5-4 平板中的非稳态传热

图5-5 无限圆柱体中的非稳态传热

图5-6 球体中的非稳态传热

对于有限固体，如有限圆柱体（圆形罐）或砖形体（矩形罐，面包条）中非稳态传热的情形，可以进行求解。这些形状可被视为无限体的集合。砖形体可视为三个相互垂直的无限板交点的集合。如果θ_x、θ_y、θ_z分别是三个无限板中单向传热的解，则可得砖形体的解为：

同样地，有限圆柱被认为是无限圆柱和无限平板交点的集合。对于有限圆柱的解为：

式中 θ_brick——砖形体的解；

θ_x、θ_y、θ_z——三个互相垂直的无限板中单向传热的解；(www.xing528.com)

θ_{finite cyl.}——有限圆柱的解；

θ_slab——无限平板的解；

θ_{infinite cyl.}——无限圆柱的解。

此即纽曼定律（Newman's Law），同样适用于质量传递。

假设主要传热阻力位于界面，而体内阻力可以忽略不计，N_Bi≈0。在实际操作中，夹套对内部湍动充分的液体进行加热即对应此种情况。由于液体混合良好，同一时刻不同位置的温度相同，但会随时间发生变化。因为此时温度仅是时间的函数，所以用常微分方程足以描述能量守恒。传热的能量守恒方程如下：

式中 V——液体体积，m³；

S——传热面积，m²。

在t=0和t=t间积分可得：

即：

[例5-3] 非稳态传热方程对香肠热加工过程温度—时间的预测（Pereira J A、Ferreira-Dias S、Dionísio L，et al，2017）。

本案例以香肠食品的热加工为例，对对流传热中一些关联式的应用进行阐述。

Morcela de Arroz（MA）是葡萄牙一种受欢迎的传统即食香肠，其中不添加商业防腐剂且保质期较短（0~5℃，7d）。香肠在烹饪加工过程中要放入汤汁中煮熟，同时达到杀菌效果，这个步骤是确保避免食源性微生物安全危害发生的关键。因此，了解香肠在热加工过程中的温度变化，对于保证产品安全并优化热过程至关重要。

视香肠为圆柱形，其浸没在热流体中发生的是非稳态的对流传热现象。为了获得对流传热系数h，首先查阅资料获得MA的相关物性参数（导热系数k、黏度μ、密度ρ、比热容C_P等），见表5-6。然后联立相应的对流传热经验关联式（5-40）以及Nu、Pr、Gr的定义式（5-41）、式（5-42）、式（5-43）对对流传热系数h_c进行求解，这四式统称为非稳态传热方程（Unsteady-State Heat Transfer Equations，USHTE）。

表5-6 MA的热物理参数

将表5-6中的参数依次代入式（5-42）和式（5-43），求出Pr和Gr，再代入式（5-40）求出Nu，结果见表5-6，在热加工过程中MA的特征长度取0.247m，则由式（5-41）可得：

换算可得h_c=100.548W/（m²·K）。

利用所求得的对流传热系数h_c，结合用于确定温度分布的海斯勒（Heisler）图表可以获得预测的温度—时间分布。在香肠中安置热电偶并连接到实时数据采集系统，可以得到热处理实验过程中每分钟的温度数据。产品中心的预测温度和达到该温度所需的时间以及实验测量值如表5-7所示。

表5-7 MA所达到的最大烹饪温度和所需时间的实验值与预测值

通过方差分析比较温度—时间分布的实验值和预测值（统计显著性设定为P<0.05）。观察到USHTE预测的时间—温度数据与实验时间—温度数据表现出良好的一致性。

研究表明，运用非稳态传热方程预测产品中心的温度和达到烹饪温度所需的时间具有一定的充分性，和实际情况相差不大，这样就无需对MA内部温度进行连续监控。同时，预测MA加热过程的持续时间要长于加热时长的阈值，这对于产品的食用和保藏安全性都是有利的。

[例5-4] 液体食品（牛乳、橙汁）非稳态传热过程中心温度的变化（吴大伟，等，2010）。

液态食品加工在生产和生活中都极为常见，其热加工过程涉及非稳态传热，了解非稳态导热过程对应用加工具有重要的指导意义。该案例以常见的液体食品牛乳、橙汁为对象，分析了非稳态传热的应用。

对牛乳、橙汁进行水浴杀菌，分别采用圆柱体和长方体容器盛装牛乳或橙汁，并密封，再分别用水浴温度50、60、70℃进行加热。其原理为一个物体侵入温度为T_∞的恒温流体浴之中，该物体初始温度为T₀，这时物体内的传热是非稳态传热，结果使物体内温度逐渐趋向T_∞，直到达到平衡为止。首先根据非稳态传热理论建立数学方程，再通过实验所得数据拟合以确定数学方程中的常数，从而获得圆柱体和长方体在非稳态传热条件下，食品中心温度随时间变化的关系式。

首先以被加热物体为液体圆柱体的情形进行推导：

如果内阻忽略，则传热过程符合式（5-38）由于实际情况的内阻不可忽略，则引入校正系数ξ，式（5-38）变为：

设定边界条件，式（5-44）进行积分，则有：

进一步等号两侧取自然对数，得：

若圆柱体半径为r，长度为L，则：

对于被加热的液体圆柱体，上式变为：

式中 K_o——以外表面为基准的总传热系数，W/（m²·K）；

h_o——圆筒壁外表面的对流传热系数，W/（m²·K）；

h_i——圆筒壁内表面的对流传热系数，W/（m²·K）；

δ——圆筒壁厚度，m；

λ——圆筒壁的导热系数，W/（m·K）；

r_o——圆筒壁的外半径，m；

r_i——圆筒壁的内半径，m；

r_m——圆筒壁的对数平均半径，m。

令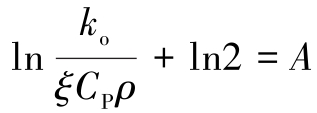，同时引入校正系数B，则上式变为：

由同样的方法可得被加热物体为液体长方体的方程：

式中 T_∞——介质流体温度，K；

T₀——被加热物体初始温度，K；

T——被加热物体中心的温度，K；

t——物体加热时间，s；

B——加热时间校正系数（与物性参数有关）；

a、b、h——分别为长方体的长、宽、高，m。

将纯净水充满圆柱体容器并密闭，置于50℃水浴中加热以模拟杀菌过程。由实验数据拟合得到圆柱体中心温度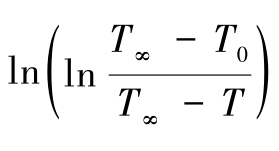与加热时间lnt的关系式为y=0.8268x-4.7307。结合式（5-51）得：解得：A=- 8.1724

其他液体食品在其他温度下的常数值可由相同的方法获得，求得平均常数值即可用于一定温度范围内适用的方程式。

在T_∞为50~70℃范围内，被加热物体为圆柱体的非稳态传热公式，当物料为牛乳时为式（5-53）；当物料为橙汁时为式（5-54）。被加热物体为长方体的非稳态导热公式，当物料为牛乳时为式（5-55）；当物料为橙汁时为式（5-56）。

上述公式为食品非稳态加热过程提供了较便捷的公式，可用于液体食品热杀菌工艺的预测。