化学反应速率及其影响因素的研究——反应动力学

反应动力学，又称化学动力学（Chemical Kinetics），研究化学反应速率以及各种因素对化学反应速率的影响。化学动力学包括研究不同的反应条件如何影响化学反应的速度，并获得有关反应机制和过渡态的信息，以及建立描述化学反应特征的数学模型。

要研究反应速率就必须了解质量作用定律（Law of Mass Action）。质量作用定律于1867年由G.W.Guldberg与P.Waage提出，其定义为：化学反应速率与反应物的有效质量成正比，其中的有效质量实际是指浓度。基元反应遵循质量作用定律，但整体反应的速率定律必须结合各个基本步骤的速率定律推导出来，相当复杂。在连续反应中，限速反应通常决定反应动力。在连续的一级反应中，近似稳态可以简化反应速率定律。反应的活化能通过阿伦尼乌斯方程（Arrhenius Equation）和艾林方程（Eyring Equation）的实验确定。影响反应速率的主要因素有反应物的物理状态、反应物的浓度、反应发生的温度以及反应中是否存在催化剂。

速率方程显示了反应速率对反应物浓度和其他物质浓度的依赖关系。根据反应机制，由不同的数学形式表征。实验确定了反应的实际速率方程，并反映出反应机制的信息。速率方程的数学表达式通常由式（2-1）给出：

式中，r是速率。x和y为反应的分级数，称反应对物质A为x级，对物质B为y级，x+y称为反应级数。c_A和c_B为反应物的摩尔浓度。k是反应速率常数，要通过实验求得。

基元反应是一种简单反应，其中一种或多种化学物质直接反应一步形成产物，并且只有一个单一的过渡态。在实际操作中，如果没有检测到反应中间体或需要假设反应在分子水平上描述该反应，则假定该反应为基元反应。一个表面看起来是基元反应的反应实际上可能是一个逐步反应，即一系列复杂的化学反应，其反应中间体的寿命是可变的。

在单分子基元反应中，A分子解离或异构形成产物：

在恒定温度下，其反应速率与A物质的浓度成正比：

在双分子基元反应中，两个原子、分子、离子或自由基，A和B，一起反应形成产物：

在恒定温度下，其反应速率与物质A和B的浓度乘积成正比：

非基元反应由一系列基元反应组成。其中每个基元反应的动力学都会影响总变化的速率，而非基元反应往往被视为一个黑箱，只考虑反应物进入黑箱的消失速率或最终产物的生成速率。我们把非基元反应称为整体反应。美拉德反应中黑色素的形成或微生物的热失活都是非基元反应。美拉德褐变速率通常表示为中间分子[如羟甲基糠醛（Hydroxymethylfurfural，HMF）]的生成速率。食品加工中大多数反应都属于整体反应类型。

化学反应的速率定律或速率方程是将反应速率与反应物的浓度或压力以及常数参数（通常为速率系数和部分反应级数）联系起来的方程。对于许多反应，速率由式（2-1）给出。式中c_A、c_B分别表示A、B两种物质的浓度，通常以mol/L表示。x和y是A和B的部分反应级数，整个反应级数是指数的和。在单分子反应中，分子A可逆生成B。

该反应中A的消耗速率可以表示为：

式（2-7）中的指数n称为反应级数，反应级数通常是正整数，但也可能是零、小数或负数。常数k是反应速率常数或者反应速率系数，单位与反应级数有关。其值可能取决于温度、离子强度、吸附剂的表面积或光辐照等条件。

基元（单步）反应的反应级数等于每种反应物的化学计量系数。总的反应级数，即反应物的化学计量系数之和，总是等于基元反应的分子数。复杂（多步）反应的反应级数可能等于或不等于它们的化学计量系数。下面以零级、一级、二级反应为例推导相关速率方程。

（一）零级反应

零级反应对应式（2-7）中n=0的情况，其反应速率与反应物消耗速率相等，且与反应物的浓度无关，即

对式（2-8）两边积分得零级反应的动力学方程：

由式（2-9）可知，对于零级反应，底物量与时间呈线性相关（图2-1）。在该动力学方程中反应速率常数k的量纲为mol/（L·s）。

图2-1 零级反应动力学A-t关系曲线

在食品变化中零级反应并不常见，尤其是生成的产物量仅为反应物量的一小部分或是仅有少量的产物由反应物形成时，反应物过量，即反应速率与反应物浓度无关，可以看作零级反应。某些情况下的非酶褐变、焦糖化以及脂质氧化都属于零级反应。

（二）一级反应

一级反应（图2-2）即n=1，反应速率与反应物浓度的一次方成正比，其速率方程如下：

等式两边积分得：

在一级反应中，反应速率常数k的量纲为s^-1，其在数值上等于时间常数（τ）的倒数，即k=1/τ，时间常数是随时间呈指数形式变化系统中的固定参数，时间常数越大，系统反应越慢。食品中的一级反应包括维生素C（抗坏血酸）的降解，食物颜色的褪去，热加工过程中食物质地的软化等。

图2-2 一级反应动力学A-t、ln（A/A₀）-t曲线

[例2-1] 维生素C（抗坏血酸）在加工过程的降解反应。

已知维生素C在加工过程中的降解过程符合一级反应动力学。假设在116℃下，维生素C的破坏以时间常数为67min的指数形式变化。若维生素C初始含量为50mg/100g食物，那么要保证116℃加工30min后剩余维生素C含量为40mg/100g食物，则初始每100g食物需要额外添加多少毫克维生素C？

解：已知维生素C降解反应符合一级反应动力学，则t时间剩余维生素C的量由式（2-11）得到：

c_A=c_A0e^-kt

其中，速率系数k是时间常数的倒数，即k=1/τ=1/67/min。

若要保证加工30min后剩余维生素C量至少40mg/100g食物，则初始维生素C含量应为：

那么，需要添加的维生素C量为：

62.6-50=12.6（mg/100g食物）

（三）二级反应

二级反应（图2-3）的n=2，反应速率与反应物浓度的平方成正比：

等式两边积分得：

图2-3 二级反应动力学c_A-t、（1/c_A-1/c_A0）-t曲线

在二级动力学反应中，速率常数k的量纲为L/（mol·s）。二级反应最为常见，如乙烯、丙烯、异丁烯的二聚反应，乙酸乙酯的水解，甲醛的热分解等，都是二级反应。

（四）多反应物/产物的速率方程

两个反应物、两个产物的反应：

该反应的反应速率表示如下：

例如，醋酸的生产：

C₂H₅OH+O₂→CH₃COOH+H₂O

则醋酸的生成速率可表示为：

（五）多步反应

以下面的反应为例：

A、B、P的浓度变化曲线如图2-4所示。

图2-4 多步反应中各反应物与产物浓度随时间变化曲线

从基本反应的准稳态假设出发，通常可以从理论上推导出具有多步反应机制的反应速率方程，并与实验速率方程进行比较，以验证所假设的反应机制。这个方程可能包含一个分数级，并且可能取决于中间物质的浓度。

如果速率不是简单地与反应物浓度的某次方成正比，那么反应对反应物的反应级数则很难确定。例如，在吸附分子间的双分子反应速率方程中的反应级数无法讨论，如式（2-18）所示。

式中 c_A，c_B——反应物A、B的浓度，mol/L；

k₁，k₂——反应速率常数，s^-1。

反应的级数不能从反应的化学方程式推导出来，必须通过实验来确定。

温度通常对化学反应的速率有很大的影响。温度较高的分子有更多的热能。虽然在较高温度下碰撞频率较大，而仅这一点对反应速率的增加贡献很小。化学反应速率常数与温度的关系可以用阿伦尼乌斯方程（Arrhenius Equation）表示：

式中 k——温度为T时的反应速率常数；

A——指前因子，又称阿伦尼乌斯常数，其单位与k相同；

R——通用气体常数，8.314J/（K·mol）；

T——热力学温度，K；

E_a——表观活化能，J/mol。

活化能实际上代表反应速率对温度变化的敏感性。如果k₁和k₂分别表示温度T₁和T₂下的反应速率常数，另一种形式是：

阿伦尼乌斯方程的图形表示如图2-5所示：

图2-5 阿伦尼乌斯方程中lnk-1/T关系曲线

当反应速率常数遵循阿伦尼乌斯方程，lnk对1/T给出了一条直线，其斜率和截距可以用来确定E_a和A。这一过程在化学动力学实验中非常普遍，常用来计算反应的活化能。

[例2-2] 烹饪对牛肉中维生素B₃（烟酸）和维生素B₆（吡哆胺）损失的影响。

维生素B₃和维生素B₆参与各种代谢功能，如维生素B₃在生物体的氧化还原反应中充当辅酶，维生素B₆参与氨基酸代谢中的氨基酸转移反应。肉制品中含有丰富的维生素B₆和维生素B₃的前体物质，但烹饪会造成二者的损失。由于加热方法的不同，文献数据无法用于预测肉类B族维生素的损失。此外，纯实验方法的应用非常有限，因为它不能考虑所有的实际可能情况：切肉尺寸、烹饪过程、设备边界条件等，因此建模是一个很好的解决这种情况的方法，A. Kondjoyan等用动力学模型的方法研究了烹饪对牛肉中维生素B₃和维生素B₆损失的影响。

模型中假设维生素的损失只发生在液相中，蒸发不会造成这些损失。此外，由于实验是在水浴或注入蒸汽条件下进行的，因此在实验过程中蒸发可以忽略或非常有限。

在这些假设下，假设肉制品的热扩散系数D恒定，则产品的温度为：

肉中B族维生素浓度的局部变化依赖于汁液排出和热变性：

式中，c为肉类中维生素B₃和维生素B₆的局部浓度，以干基表示。汁液损失与水分排出有关，肉类内部水分含量X的变化也以干基表示，计算公式见式：

式中，k_排出（T，d）依赖于局部肉温以及从采样点位置到肉块表面的距离。这里没有给出描述这种依赖关系的函数和参数。X_eq（T）为“无限加热时间”后得到的平衡含水量；当X=X_eq（T）时即停止排汁。利用这一结果，测定了汁液排出引起的维生素浓度的局部变化：

式（2-24）中c_汁液是排出汁液中B族维生素的浓度，以肉类干物质为基础表示。

假设肉类中B族维生素的热变性速率（dc/dt）遵循一级动力学，变性反应速率常数k_热变性通过阿伦尼乌斯方程依赖于肉类局部温度。当变性的机制还不完全清楚的时候，一级反应是经典假设的最简单模型，这里就是这种情况。

在这些假设下，通过加入式（2-23）和（dc/dt）_热变性，由汁液排出和热变性引起的维生素B浓度的局部变化为：

当X=X_eq（T）不再排出时，B族维生素的损失仅仅是热变性造成的。考虑到c_汁液的值是恒定的，分析了c_汁液对B族维生素损失的影响。这一假设后来得到了验证，它与本书所采用的简化方法一致，如对传质模型的简化方法。这是合理的，因为从文献中得知，汁液的排出比B族维生素的热变性要快。c_汁液在实验的第一步进行评估，在参数识别过程中可以在0.1c₀和c₀之间变化。假设汁液中B族维生素的浓度（以肉类干物质为基础表示）不能高于肉类中B族维生素的浓度，而选择0.1c₀是为了确保汁液中B族维生素的浓度高于该值。通过计算肉的局部温度T，将传热模型与传质模型结合式（2-24）~式（2-25）。传热模型采用诺伊曼（Neumann）边界条件。

物理过程通常会导致食品质量变化，如乳状物分层、沉淀、破碎、黏度变化、生物聚合而发生的凝胶化、结晶和水分迁移等。由于这些物理变化更加复杂，并且可能伴有化学变化，因此建立针对这些物理现象的数学模型比较困难。

介绍两个预测分散体系黏度的模型，一个是由Einstein推导的稀释分散体的方程：

式中 η——分散体系的黏度，Pa·s；

η_s——溶剂的黏度，Pa·s；

φ——相所占的体积分数（相对于总体积），%。

这个公式中，只有φ对于黏度有重要的影响，而颗粒的大小对其没有影响。然而此公式只适用于很稀的分散体系中（φ<0.01），因此不是很适合于食品体系。对于更多的高浓度分散体系中，经验关系式埃勒斯（Eilers）方程适用：

式中 φ_max——假设的可能被紧密堆积的具有代表性颗粒占用的最大体积分数，%。

式（2-28）中相关符号同式（2-27），该式在食品体系中非常好用。例如，可以应用于预测含有不同体积分数的酪蛋白胶粒的脱脂牛乳的黏度，也可用来描述分散颗粒对酪蛋白酸盐复合材料的形变性能影响。因此，只要知道分散颗粒的体积分数，就可运用式（2-28）预测食品的流变性质。

还有一些数学模型用来描述物理现象，如聚集和絮凝、结晶动力学、干燥和脱水等。需要注意的一个关键点是，物理的质量指标经常涉及简单的化学反应，如食品的质构变化。例如，在马铃薯的烹饪过程中组织软化的原因是由非常复杂的过程导致的，其中一个原因是果胶降解。上述现象可以建立一阶动力学模型，然后在阿伦尼乌斯方程中估算出速率常数，随后推导出活化能。

酶催化反应的机制是降低反应的活化能，加快反应速率。酶催化反应受很多因素影响，如温度、pH、酶和底物的浓度、激活剂、抑制剂等。底物浓度的改变，对酶催化反应速度的影响较为复杂，可以用米氏方程表示：

式中 V——反应速率，mol/（L·s）；

V_max——酶被底物饱和时的反应速率，mol/（L·s）；

K_m——米氏常数，mol/L；

S——底物浓度，mol/L。

米式方程的图形表示如图2-6所示：

图2-6 米氏方程中V-c_s关系曲线

如图2-6所示，酶促反应过程中，当底物浓度低时，酶促反应为一级反应；当底物浓度在中间范围时，酶促反应为混合级反应；当底物浓度继续增加时，酶促反应由一级反应向零级反应过渡。

在一定的温度和pH条件下，当底物浓度足以使酶饱和时，酶浓度与酶促反应速度呈正比关系如图2-7所示。

图2-7 底物浓度使酶饱和时酶浓度与酶促反应速度关系曲线

温度影响酶促反应的速度，在一定范围内，反应速度随温度升高而加快。温度超过一定范围后，酶受热变性的因素占主导，反应速度随温度上升而减慢。通常将酶促反应速度达到最大的某一温度范围称为酶的最适温度（图2-8）。

图2-8 温度对酶反应速率的影响

pH对酶促反应的影响类似于温度对酶促反应的影响，也为钟罩形曲线（图2-9）。pH影响酶活性中心的解离状态从而影响酶反应速率，过酸、过碱影响酶分子的结构，甚至使酶变性失活。因此，在食品工业中可以通过调整pH来控制酶活力。

图2-9 pH对酶反应速率的影响

酶制剂在食品工业中广泛应用，如利用木瓜酶的酶促反应，把食品中的大分子营养物质蛋白质、脂肪、纤维素等水解成小分子物质氨基酸或多肽；利用葡萄糖氧化酶代替化学氧化剂和脂肪酶强化面筋，使面团更稳定，面包品质更好；在葡萄酒工业中，涉及淀粉酶、糖苷酶、纤维素酶、葡聚糖酶、半纤维素酶、果胶酶、蛋白酶、葡萄糖氧化酶和过氧化氢酶等的应用。酶促反应具有高效和高特异性的特点。

[例2-3] 乳脂肪酶解动力学（Irene Peinado，2018）。

胰腺功能不全是一种临床表现，其特征在于胰腺不能将足够的胰酶释放到小肠中，这是消化腔内营养所必需的。消化酶的缺乏导致难以吸收营养物质，这些营养物质导致婴儿营养不良和生长发育迟缓。这些患者通常需要口服酶以促进脂肪分解并从食物中吸收脂质。然而，许多食物的相关因素（基质、脂肪类型等）和消化环境（肠道pH、胆汁浓度等）将影响营养素的消化率。pH-Stat滴定法与静态系统相结合是一种经典的研究体外消化的方法，通过直接提供反应动力学参数，可以监测“体外”消化的肠道阶段，乳化脂质的消化取决于不同的参数，如它们的组成、结构性质、界面大小、酶对界面层的亲和力等。反应速率与底物（S）和酶（E）的浓度满足式（2-30）：

式中 V——反应速率，μmol/（mL·min）；

K_cat——催化常数，s^-1；(www.xing528.com)

K_m——米氏常数，mmol/L；

S——底物浓度，mmol/L；

E₀——初始酶浓度，mmol/L。

采用体外消化模型表征了酶制剂催化乳脂肪脂解的动力学过程。以不同种类的全脂牛乳作为酶解底物，模拟不同肠道条件pH（6、7、8）和胆汁浓度（1、5、10mmol/L），使用固定浓度的补充剂。通过对不同pH和胆汁浓度下反应速率与底物浓度的关系作图，拟合到米氏方程中获得米氏常数K_m和催化常数的对应值K_cat。采用pH法成功地监测了牛乳体外消化过程中游离脂肪酸的释放。随着pH和胆汁浓度（pH 7/10mmol/L~pH 8/10mmol/L）的增加，米氏常数（K_m）降低，脂解反应速率（V）增加。获得脂肪—牛乳水解动力学的信息，可以估计底物数量，以优化酶活性补充所需的不同肠道条件下的pH和胆汁浓度。

微生物的生长是指活细胞数目的增加或生物量的增加，若生物量或细胞增长1倍的时间间隔是常数，则微生物呈指数形式增长，可以用数学模型描述。本节主要介绍微生物生长的动力学。微生物生长动力学可反映出细胞适应环境变化的能力。

罗杰斯蒂（Logistic）生长曲线最初是由比利时数学家P.F.Verhulst在1838年推导出来的，但被长期覆没，直到20世纪20年代才被R.Pearl和L.J.Reed重新发现。其特点为开始生长时较为缓慢，接着在一定范围内迅速生长，达到一定限度后又缓慢生长，曲线略显拉长的“S”形，因此也称为S曲线。其表达如式（2-31）：

式中 X——菌体浓度，g/L；

X_m——最大菌体浓度，g/L；

μ_max——最大比生长速率，s^-1；

t——时间，s。

该S曲线能够较好地反映出在分批发酵过程中由于菌体浓度的增加对菌体本身的生长抑制作用。

微生物生长曲线如图2-10所示，曲线可分为四个阶段，即迟缓期、对数生长期、稳定期和衰亡期。当微生物进入新的生长环境后，需要有一段时间来适应，在这一过程中，微生物生长缓慢，其菌体浓度基本不变，此为延缓期；微生物适应了生长环境后，由于培养基内营养丰富，且此时微生物数量少，排出的有害物质少，因此微生物进入迅速生长和大量繁殖阶段，菌体密度呈对数生长，此时进入对数生长期；一段时间的高速繁殖后，培养基内营养物质被大量消耗，有害物质逐渐积累，微生物的生长繁殖受到限制，有菌体开始死亡，新生的菌体数量与死亡的数量趋于平衡，这是稳定期的特点；当培养基内营养物质消耗殆尽，有害物质大量的积累，导致微生物不能正常的生长繁殖，菌体大量死亡，菌体密度显著下降，进入衰亡期。

图2-10 微生物生长曲线

微生物生长的动力学遵循莫诺（Monod）方程（图2-11）：

式中 μ——比生长速率，s^-1；

S——限制性基质浓度，g/L；

μ_max——最大比生长速率，s^-1；

K_s——饱和常数，为当μ=μ_max/2时的基质浓度，g/L。

图2-11 细胞的比生长速率与限制性基质浓度的关系

Monod方程是典型的均衡生长模型，其基本假设如下：

（1）细胞的生长为均衡式生长，因此描述细胞生长的唯一变量是细胞的浓度；

（2）培养基中只有一种基质是生长限制性基质，而其他组分为过量不影响细胞的生长；

（3）细胞的生长视为简单的单一反应，细胞得率为一常数。

Contois模型也可以用来表示菌体生长动力学。其表达式为：

从方程的表达式来看，Contois模型是在Monod方程的基础上，将底物抑制常数K_s乘以菌体浓度X。表明发酵过程中的抑制作用并非一成不变，而是随菌体浓度的变化而发生变化。这一点符合实际生产发酵情况，是对Monod方程的一个改进。此公式对食品工业污水处理很重要。

另外一个常用的预测食品中细菌生长能力和保质期的生长模型是修正的冈珀茨（Gompertz）模型，这是一个双指数函数，模型表述为：

式中 lnN——微生物在时间t时常用的对数值；

C——随时间无限增加时菌增量的对数值；

A——随时间无限减小时微生物的对数值（相当于初始菌数）；

B——在时间M时最大生长速率，h^-1；

M——达到最大生长速率所需要的时间，h。

Logistic模型和Gompertz模型比较适合描述适温条件下微生物的生长，这是因为较早的预测微生物学模型主要侧重于研究食品中病原菌的生长。Gompertz模型未考虑延滞期的影响，预测准确性存在问题。

巴拉尼&罗伯茨（Baranyi & Roberts）模型（以下简称Baranyi模型）的表述为：

式中 N——t时微生物数量；

N₀——初始微生物数量；

N_min——最小微生物数量；

k_max——最大相对死亡率；

r，s——参数。

该模型只考虑细胞生长过程中的一个参数。式（2-35）描述了微生物数量随时间的变化，式（2-36）描述了微生物生长延滞期阶段。该模型使用方便，模型中的参数与微生物生理状态有关，理论上，模型的参数越多，预测的准确性越高，但参数过多势必导致模型使用不便并增加工作量，而Baranyi模型既能准确预测，参数量也较少，且适用于多种情况，因此Baranyi模型在预测食品微生物领域应用的越来越广泛。

导致食品腐败变质的一个主要原因是由于微生物的生长繁殖，为了保证食品在一定货架期内的口感、风味、色泽等不发生变化，需要对食品进行灭菌处理，因此引入灭菌过程中的微生物致死曲线。

常用的灭菌方法有化学试剂灭菌、辐照灭菌、干热灭菌、湿热灭菌和过滤除菌等。无论何种灭菌方法，菌体剩余量都会随时间减少。以热灭菌为例，设定几个参数来表示灭菌过程，D值代表微生物减少90%所需的时间；Z值代表将D值降低90%所需提高的温度；F值代表在特定温度下，微生物被全部杀死所需的时间。假设灭菌开始时的初始总菌体量为N₀，每一段时间内的细菌存活概率为P，且每段时间存活概率互不影响，则t时间后菌株存活量为：

等式两边取对数，

令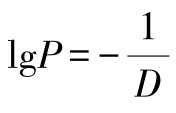，则

若令lnP=-k，由换底公式得

图2-12 一定温度下细菌存活数目的对数lgS随时间的变化情况

式（2-41）、图2-12可知，当每一段时间内的细菌存活概率P不变时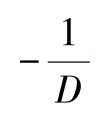，为常数，此时式（2-40）中菌株存活量与时间t的关系符合一级反应动力学模型，但由于微生物的种类多样且反应容器传热不均匀，导致每升温一定时间细菌的存活率不相等，即P值不固定，因此实际过程中的杀菌过程不属于一级反应动力学。但可以通过韦布尔（Weibull）分布校正杀菌过程的一级反应动力学。

（一）韦布尔（Weibull）分布

Weibull分布是进行可靠性分析和检验寿命长短的理论基础。在灭菌过程中微生物存活数量S（t）随灭菌时间的变化由Weibull分布表示为

式中，α为比例参数，是时间的特征参数，代表微生物数量减少90%所需的时间，与前文出现的D意义相同；β为形状参数，β的改变会导致分布曲线形状的变化（图2-13）。

对式（2-42）两边取对数，

Weibull分布是一个经验模型。其中的α、β与pH、温度、水分活度、压力、离子强度有关。

图2-13 剩余微生物数量的对数随时间的变化情况

注：α为微生物数量减少90%所需的时间。

[例2-4] 基于细菌抗药性的混合双Weibull分布，用于描述各种形状的灭活曲线的一般模型（Coroller L.，2006）。

当细菌由于不利的环境条件引起非热失活时，其存活曲线随应激的强度不同显示不同的凹凸性。怀廷（Whiting）模型可以满足部分非热失活的分析，为更好地模拟非热失活曲线，建立一种新的失活模型，将在群体的各种生理状态下的数据与Whiting的模型进行比较。

以从盐水分离的肠炎沙门菌血清型鼠伤寒沙门菌（Salmonella enterica）菌株ADQP305和从肉制品分离的单核细胞增生李斯特菌（Listeria monocytogenes）菌株SOR100为研究对象，为了研究细菌的生理状态对灭活的影响，在不同的生长阶段除去细胞。对BHI肉汤进行了改进，以产生导致失活的应激条件，将微生物接种到100mL的改良BHI肉汤中，在接种后适当的时间间隔内，对剩余微生物进行平板培养。

模型检验：

（1）Whiting模型Whiting模型来自Kamau等人提出的模型。它依赖于两个具有不同抗压水平的亚群的共存。

其中，t是时间，N₀是初始细菌浓度，f是主要亚群占初始菌群的分数，t_lag是死亡潜伏时间，k₁和k₂分别是主要亚群和次要亚群的失活率。

（2）Weibull模型 过去几十年在热处理研究和非热处理研究中，Weibull模型已被广泛用于描述细菌对热应激的抵抗力。这里提出重新参数化[式（2-45）]，并将其用于本教材研究。

其中，N是细菌存活的数量，N₀是接种量，t是时间，p是形状参数，δ是细菌量减少90%所用的时间。

为了描述各种形状的失活动力学曲线，假设群体由具有不同抗应激能力的两个亚群组成。假设每个亚群的抗性遵循Weibull分布。然后可以通过式（2-46）描述剩余细菌量：

下标1和下标2表示两个不同的亚群。亚群1对应激较亚群2更敏感（δ₁<δ₂）。f是群体中亚群1的占比。

对于从0到1变化的分数f，无法产生足够的差异。为了具有更具区别性的参数，引入了从负无穷大到正无穷大的新参数（α）：

这个方程等价于

通过该变换，当f=0.999999时对应α=4，当f=0.999900时对应α=6。这相当于亚种群2的初始大小增加了100倍。在引入该值之后，式（2-46）变为：

（3）双Weibull简化模型 当在低浓度下进行计数时，曲线的右侧部分（对应于更具抗性的亚群——亚群2）似乎是凸起的，与更敏感的亚群1的曲线相似。因此，将相同的形状参数应用于两个子群可以使模型简化。最终的模型是：

模型建立完成后，通过参数估计、置信区间等来评估模型的优越性。比较了Whiting模型和两个新提出的模型用于描述在培养期间细菌存活情况的准确性。对比发现，双Weibull简化模型更能适应多种情况，可以描述双相非线性形状（p>1），以及双相线性情形（p=1）。双Weibull简化模型的优点之一是所有模型参数都可以用图形来描述（图2-14）。双Weibull简化模型能够使细菌适用于大多数形状的失活曲线，通过使用-α或α<lg（N₀/检测限）或两个δ值之间相等将双Weibull模型简化为简单模型。

需要进一步研究以允许在非热灭活研究中使用双Weibull模型。Weibull模型的优势在于它具有很大的灵活性，因为比例参数（α）和形状参数（p）之间有很强的相关性。特别要注意的是，p取决于环境因素和细胞生理状态，在某些热处理情况下，p为常数。如果估计p在不同的应激条件下是恒定的，参数δ能够平衡这种约束条件从而提供良好的数据模型拟合度。如果这种现象可以在非热失活研究中得到验证，则应用双Weibull模型仅通过三个参数就能描述细胞生理状态与应激条件之间的动力学函数（图2-14）。

图2-14 基于双Weibull抗药性分布的生存模型图

——微生物种群 ┈┈亚群1 --—亚群2

注：亚群1代表对应激更敏感的细菌，亚群2代表更具抗性的细胞。

（二）麦克斯韦—玻尔兹曼（Maxwell-Boltzmann）分布

麦克斯韦—玻尔兹曼分布被用于描述理想气体中粒子运动速度的概率分布。理想气体可以看作除了非常短暂的碰撞（粒子之间或粒子与热环境交换能量和动量）外，粒子在固定容器中做自由运动，彼此之间没有相互作用，这类粒子的能量遵循麦克斯韦—玻尔兹曼分布，通过使粒子能量与动能相等可以得到速度的统计分布。在食品加工过程中，温度可视作样品中分子平均动能的量度，在任何温度下动能的分布都很广，因此也遵循麦克斯韦—玻尔兹曼分布。

1.麦克斯韦速率分布律

（1）速率分布函数 对某一个分子来说，其速度大小和方向完全是偶然的。但就大量分子整体而言，在一定条件下，其速度分布遵从一定的统计规律。设N个分子，速率分布于（v，v+dv）区间的分子数为dN，则

其中f（v）代表气体分子的速率分布函数

速率分布函数表示分布于速率v附近的单位速率间隔内的分子数占总分子数的比，也表示一个分子的速率处于v附近单位速率间隔内的概率。

（2）麦克斯韦速率分布函数 麦克斯韦用概率论导出，当忽略气体分子间的相互作用时，在平衡态下，气体分子的速率分布函数为：

式中 m——分子的质量，kg；

T——热力学温度，K；

k——玻尔兹曼常数，1.38×10^-23J/K；

v——速率，m/s。

如图2-15所示，dS等于分布在v附近的速率区间dv内的分子数占总分子数的比率。麦克斯韦速率分布曲线随温度变化情况如图2-16所示。

图2-15 麦克斯韦速率分布曲线

图2-16 麦克斯韦速率分布曲线随温度的变化

2.玻尔兹曼分布律

麦克斯韦速率分布律适用于无外力场作用，分子的空间密度均匀的情况。当气体处于外场中，分子在空间的分布不均匀，分子按速度和空间的分布由玻尔兹曼分布律确定。

（1）玻尔兹曼分布律 设分子系统在外力场中处于平衡态，其中dN个分子的空间位置和速度分别处于如下区间：（x，x+dx）（y，y+dy）（z，z+dz）（v_x，v_x+dv_x）（v_y，v_y+dv_y）（v_z，v_z+dv_z），则这dN个分子的分布满足下述玻尔兹曼分布律：

式中 n₀——ε_p=0处的分子数密度；

ε_p—— 位于（x，y，z）处的分子势能；

ε_k——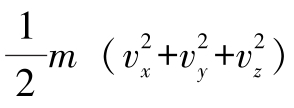，为分子动能。

（2）分子在外力场中按空间位置的分布 分子在外力场中不管分子速度如何，只考虑全体分子按照空间位置的分布规律。此时在玻尔兹曼分布中对所有速度积分得

分子密度：

结合麦克斯韦速率分布律，可以得到麦克斯韦—玻尔兹曼分布函数

在图2-16中，如果虚线表示活化能，随着温度的升高，能够克服活化能势垒的分子的比例也会增加。结果是反应速率增加。分子的这一部分可以通过表达式得到：

式中 E_a——活化能；

R——玻尔兹曼常数，同k；

T——热力学温度。

麦克斯韦—玻尔兹曼分布形成了分子运动论的基础，它解释了许多基本的气体性质，包括压强和扩散。麦克斯韦—玻尔兹曼分布通常指气体中分子的速率的分布，也可以指分子的速度、动量以及动量的大小的分布，虽然不同的分布有不同的概率分布函数，但它们之间可以存在相互联系。