坝体结构与地基动力相互作用优化方案

坝体结构与地基动力相互作用问题包含两个方面的内容,即地基的模拟和地震荷载的输入机制。长期以来,大坝动力法的地震反应分析一直沿用Clough教授提出的人工截断无质量地基边界均匀输入模型,该模型虽然得到了工程界的广泛认同和应用,但其本身存在两个问题:其一,人工截断边界必然带来对地震能量的虚假反射,亦即不能反映坝体振动能量向无限域地基的散逸,使计算所得的坝体动力反应被人为夸大;其二,没有考虑地震波传播所造成的坝基河谷各点地震动的差异,而这种差异可能会对建在宽河谷高拱坝的动力响应带来不容忽视的影响。

为了克服上述两个方面的缺欠,近年来国内外学者做了大量研究探讨工作,并取得了一些可喜的进展,尤其是我国科技工作者通过“七五”至“九五”连续科技攻关,在这一领域获得的成果已接近或达到国际先进水平。为了在动力反应分析中考虑无限地基辐射阻尼效应,各国学者已相继提出了多种模拟计算方法。

(1)局部透射边界。Lysmer(1969)最早提出了一种粘性边界,通过沿人工边界设置一系列阻尼元件来吸收射向人工边界的波动能量,粘性边界物理概念明确,方法简单、直观,且适宜与有限元法结合,但对波的吸收仅有一阶精度,不够精确;随后,White(1997)、Akiyoshi(1998)和Liu等人在Lysmer工作的基础上,为了提高粘性边界的计算精度和适用性,又分别发展了统一边界、协调粘性边界和粘弹性边界。廖振鹏等人通过外插人工边界上各点在当前时刻和前一时刻的位移来消除外行波的反射,从而提出了一种暂态透射边界,并利用一阶透射后的误差仍为平面波的特性建立了多次透射公式,这种边界是一种时域局部人工边界,物理概念清晰,数学处理方便,有较高的精度,易于与有限元法结合,可以考虑域内的非线性问题,具有较好的应用前景。中国水科院陈厚群等人已将其应用于拱坝—地基—库水系统的非线性地震响应分析。

此外,近年来各国学者还提出了一些其他的局部透射边界,如Keys(1985)、Higdon提出的多向透射边界,Wolf和Song提出的双渐近多向透射边界等。综观以上所述及的各种局部人工边界,虽然各有其优点和适用范围,所依据的物理概念和使用的数学处理工具也不尽相同,但都存在低阶边界精度不高和高阶边界稳定性差的问题。然而,由于局部人工透射边界的计算效率较高,易于与有限元或有限差分等数值方法结合,并且能够处理非线性问题,因而在高坝地震动力响应分析中还是得到了较为广泛的应用。

(2)无限元法。采用有限元与无限元耦合系统可以在坝体结构-地基相互作用分析中,计入无限地基的辐射阻尼,以及由近场到远场介质条件的变化。无限元法作为有限元法的延伸,它是通过在形函数中引入波状衰减因子来反映波向无限远处的传播。无限元概念是由Ungless(1973)等人首先在静力学领域提出的,开始时是以指数形式的衰减因子构成形函数的。随后,Bettess和Zienkiewicz等人在形函数中引入波动因子,提出了最初的动力无限元,1985年又发展提出了映射无穷元,直接利用几何映射关系导出r-1幂级数形式的衰减因子,使之更加符合实际。

虽然无限元法已在模拟无限域地基方面得到了广泛应用,但该法仍存在一些缺欠,如无限元法的精度在很大程度上取决于径向形函数的选取,形函数的阶数较低时,为了获得较高的精度就需要将无限元置于较远处,从而使系统求解的规模扩大;而提高径向形函数的阶数,固然会有助于求解精度的提高,但这样又有可能导致方程的病态。(www.xing528.com)

(3)边界元法。由于边界元可以自动满足无穷远处的辐射条件,不存在人工边界的反射问题,因而在处理无限域和半无限域问题中具有特殊的优越性,在坝体结构-地基动力相互作用分析中得到了广泛的应用。Dominguez(1978)首先将频域边界元法用于求解二维和三维表面式及嵌入式基础的动力刚度与波动响应。Karabalis和Beskos(1984)等人则用时域边界元法研究了地基动力刚度和波动响应问题。利用边界元与有限元耦合是分析结构与地基动力相互作用的有利工具,最早实现频域内有限元和边界元耦合的是Toki和Sato(1977);随后Underwood(1981)、Mita(1983)、Kobayashi(1985)、Gaitanareos等人在有限元和边界元频域耦合研究方面都作出了有意义的贡献;Karabalis则将这一耦合技术发展到时域中;Wolf又提出了将频域地基动力刚度转换为时域动力刚度的方法,从而实现了频域和时域两大类方法的耦合。

在应用边界元法求解坝体结构-地基动力相互作用问题时,既可采用全空间动力基本解(Green函数),也可采用半空间基本解。半空间基本解是由Banerjee(1990)等人导出的,解的形式很复杂,在实际应用中较为困难,但它可以自动地满足地表边界条件。而全空间基本解计算比较简单,但是在用它求解半空间域的工程问题时,由于全空间Green函数不能满足半无限地基上表面的边界条件,因此需要将地表离散到相当长的距离,然后截断,这样为了保证计算精度,则要取足够大的离散范围,从而使计算工作量大增。为了充分利用全空间Green函数的简单性,又不致于增加边界元的离散范围,张楚汉、金峰等人提出了一种无限边界元(IBE),用于模拟从近场到远场的近似位移,从而大大减小了离散距离,节省了计算工作量,并将这种单元与边界元、有限元耦合起来,成功地研究了重力坝和拱坝坝体结构-地基的动力相互作用问题,拱坝-地基系统的FE-BE-IBE模型如图8-7所示。

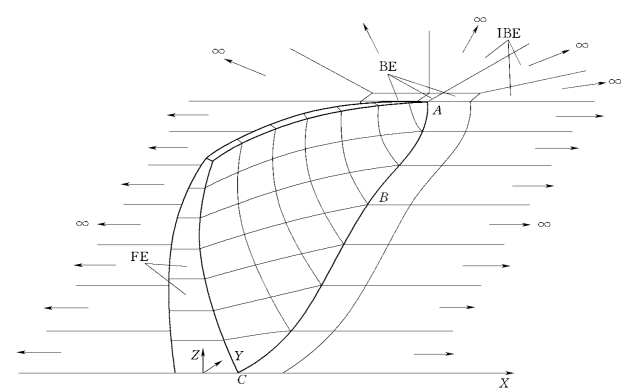
图8-7　拱坝-地基系统的有限元-边界元-无限边界元模型

(4)其他方法。可用于求解结构-地基动力相互作用的数值计算方法,除了上述三种主要方法外,还有边界法、一致边界法、克隆算法(Cloning)等。其中克隆算法是基于相似原理,在有限元法基础上发展起来的一种新型数值分析方法。这种方法类似于边界元法,仅需离散计算域的边界而无限远处的辐射条件可以自动满足,但它不需要基本解,因而在模拟无限地基方面具有更为广泛的应用前景。单层克隆算法是Dasgupta(1982)首先提出的,随后Wolf等人通过对无限地基动力刚度做无量纲频率的台劳展开,又提出了可处理嵌入式地基的广义克隆算法,但该法数值求解存在一定的难度,限制了它的实用性。之后,Wolf又将广义克隆算法的思想引入时域,提出了一致无穷小的有限单体法;进而又基于坐标变换和加权余量技术重新推导了弹性动力学问题的基本方程,并将此法命名为比例边界有限元法(SBFE)。SBFE方法是一种半解析方法,它融合了边界元和有限元两大数值方法的优点,今后有可能被广泛用于结构-地基动力相互作用问题的分析研究中。