驻波与行波的互动关系

驻波和行波之间，在一定的条件下，是可以互相转换的。这种特点，在电机学里得到了充分的应用。分述如下：

3.1.3.1 驻波可以分解成行波

1.数学推导

根据三角学里“积化和差”的公式，式（3-3）可以分解为

式中 Φ（x，t）———在驻波磁场中，某一瞬间在某一位置的磁通，Wb；

Φ₁———磁通的行波分量之一，Wb；

Φ₂———磁通的行波分量之二，Wb。

式（3-9）表明，驻波磁通可以分解为两个行波磁通Φ₁和Φ₂。式中的“-”号说明，在起始位置（x=0）时，Φ₁和Φ₂是相等而方向相反的，如图3-6所示的那样。但就宏观效果而言，这里的“-”号或“+”号的实际效果是没有什么区别的。

2.图解

如图3-6所示，Φ₁是顺时针方向的行波磁通，Φ₂是逆时针方向的行波磁通，当它们以相反的方向旋转时，合成磁通就是驻波。

图3-6 驻波磁通分解成行波磁通

3.应用

驻波磁场可以分解成两个方向相反的行波磁场的原理在分析单相异步电动机时得到了充分的应用。

3.1.3.2 驻波也可以合成为行波(www.xing528.com)

在两个互相垂直的绕组里，让其中一个（β相绕组）和电容器串联，如图3-7a所示，今假设两个绕组里的电流振幅值相同，如图3-7b所示：

当ωt=0时，Φ_α=0，Φ_β=Φ_m，合成磁通等于Φ_β，如箭头①所示；

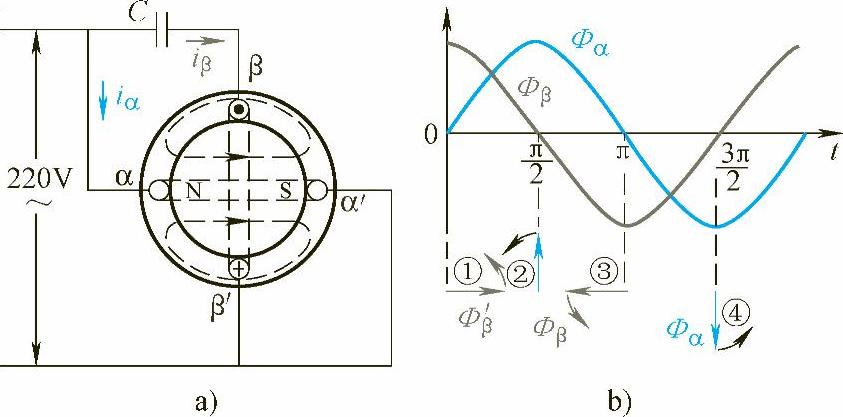
图3-7 驻波磁场合成为行波磁场

a）两个互相垂直的驻波磁通 b）合成磁通

当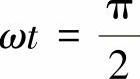时，Φ_α=Φ_m，Φ_β=0，合成磁动势等于Φ_α，如箭头②所示，比前头①逆时针旋转了90°；

当ωt=π时，Φ_α=0，Φ_β=-Φ_m，合成磁通又等于Φ_β，如前头③所示，比前头②又逆时针旋转了90°；当时，Φ_α=-Φ_m，Φ_β=0，合成磁通如前头④所示，比前头③又逆时针旋转了90°。

可见，这合成磁通也是行波磁通。

在实际工作中，两个绕组里的电流振幅值常常是不相等的，两个磁通的振幅值也就不一样，如图3-8a所示。

图3-8 椭圆旋转磁场

a）两电流振幅不等 b）椭圆旋转磁场轨迹

结果是，行波磁场的末端轨迹是椭圆形，如图3-8b所示，称为椭圆旋转磁场。

单相异步电动机就是利用椭圆旋转磁场来获得起动转矩的。