变频器矢量控制原理

变频器的矢量控制是20世纪70年代开始迅速发展起来的一种新型控制思想，是以电动机控制参数的实时解耦，来实现电动机的转矩与磁通控制，以达到与直流电动机一样的调速性能。异步电动机矢量控制调速系统经过近几十年的发展，其控制方法已趋成熟。

1.基本原理

异步电动机的矢量控制是仿照直流电动机的控制方式，把定子电流的磁场分量和转矩分量解耦开来，分别加以控制，即将异步电动机的物理模型等效地变成类似于直流电动机的模式。

众所周知，交流电动机三相对称的静止绕组A、B、C，通以三相平衡的正弦电流时，所产生的合成磁动势是旋转磁动势F，它在空间呈正弦分布，以同步转速ω（即电流的角频率）顺着A—B—C的相序旋转。这样的物理模型绘于图4-14a中。

然而，旋转磁动势并不一定非要三相不可，除单相以外，二相、三相、四相……等任意对称的多相绕组，通以平衡的多相电流，都能产生旋转磁动势，当然以两相最为简单。如图所示图4-14b中绘出了两相静止绕组α和β，它们在空间互差90°，通以时间上互差90°的两相平衡交流电流，也产生旋转磁动势F。当图4-14a和b的两个旋转磁动势大小和转速都相等时，即认为图4-14b的两相绕组与图4-14a的三相绕组等效。再看图4-14c中的两个匝数相等且互相垂直的绕组M和T，其中分别通以直流电流i_M和i_T，产生合成磁动势F，其位置相对于绕组来说是固定的。

图4-14 交流电动机绕组等效

a）三相交流绕组 b）二相交流绕组 c）旋转的直流绕组

如果让包含两个绕组在内的整个铁心以同步转速旋转，则磁动势F自然也随之旋转起来，成为旋转磁动势。把这个旋转磁动势的大小和转速也控制成与图4-14a和图4-14b中的磁动势一样，那么这套旋转的直流绕组也就和前面两套固定的交流绕组都等效了。当观察者也站到铁心上和绕组一起旋转时，在他看来，M和T是两个通以直流而相互垂直的静止绕组。如果控制磁通的位置在M轴上，就和直流电动机物理模型没有本质上的区别了。这时，绕组M相当于励磁绕组，T相当于伪静止的电枢绕组。

由此可见，以产生同样的旋转磁动势为准则，图4-14a的三相交流绕组、图4-14b的两相交流绕组和图4-14c中整体旋转的直流绕组彼此等效。或者说，在三相坐标系下的i_A、i_B、i_C，在两相坐标系下的i_α、i_β和在旋转两相坐标系下的直流i_M、i_T是等效的，它们能产生相同的旋转磁动势。

有意思的是：就图4-14c的M、T两个绕组而言，当观察者站在地面看上去，它们是与三相交流绕组等效的旋转直流绕组；如果跳到旋转着的铁心上看，它们就的的确确是一个直流电动机模型了。这样，通过坐标系的变换，可以找到与交流三相绕组等效的直流电动机模型。

2.矢量控制框架与坐标变换

图4-15所示为矢量控制的基本框架，即将异步电动机按照等效直流电动机模型进行控制。

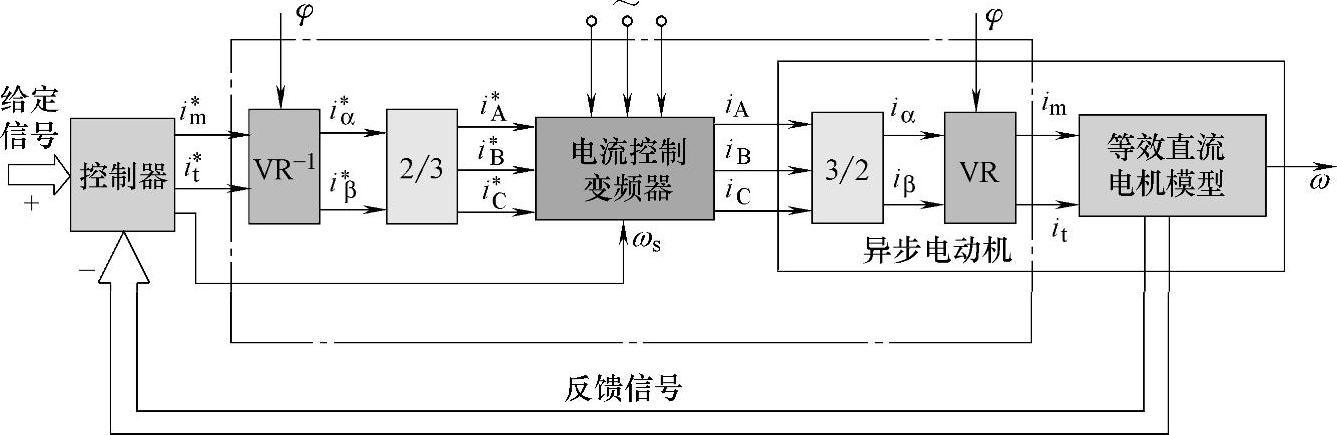
图4-15 矢量控制基本框架

图4-16中要涉及多个坐标变化，包括2/3相变换、2s/2r变换、K/P变换等。

（1）3/2相变换和2/3相变换

在三相静止绕组A、B、C和两相静止绕组α、β之间的变换，称为三相静止坐标系和两相静止坐标系间的变换，简称3/2相变换。反之，则称为2/3相变换。

（2）2s/2r变换和2r/2s变换

从两相静止坐标系α、β到两相旋转坐标系M、T变换称作两相-两相旋转变换，简称2s/2r变换，其中s表示静止，r表示旋转。反之，则称为2r/2s变换。

（3）K/P变换

令矢量i_s和M轴的夹角为θ_s，已知i_M和i_T，求i_s和θ_s，就是直角坐标/极坐标变换，简称K/P变换（见图4-16）。

了解了坐标变换后，就可以理解矢量控制的主要步骤：要把三相静止坐标系上的电压方程、磁链方程和转矩方程都变换到两相旋转坐标系上来，可以先利用3/2相变换将方程式中定子和转子的电压、电流、磁链和转矩都变换到两相静止坐标系α、β上，然后再用旋转变换阵C_2s/2r（图4-15中的VR），将这些变量变换到两相旋转坐标系M和T上。(www.xing528.com)

因此，从图4-16中可以这样认为，在控制器后面引入的反旋转变换器VR⁻¹与电动机内部的旋转变换环节VR抵消，2/3变换器与电动机内部的3/2变换环节抵消，如果再忽略变频器中可能产生的滞后，则图中虚线框内的部分可以完全删去，剩下的就是直流调速系统了。

图4-16 矢量控制坐标变换

3.转子磁场定向下的异步电动机数学模型

矢量控制就是通过坐标变换，实现定子侧控制量的解耦，该方法是分析异步电动机数学模型，简化电磁关系，实现控制系统设计的有效手段。由于转子磁场定向旋转坐标系下异步电动机数学模型意义明确、简化实用，常用于设计调速控制系统。

在转子磁场定向矢量控制下，其电压矢量与电流矢量之间的方程矩阵形式如下所示：

式中 R_s/R_r为定子/转子电阻；L_s/L_r为定子/转子漏感抗；L_m为互感抗；ω_s1为角速度；p为微分因子。

显然，可以想象得出，异步电动机参数对于矢量控制的重要性，因此在很多矢量控制变频器中都含有自动检测电动机参数的程序，以防止用户输入电动机参数不准确所带来的控制精度误差。

4.电动机参数的调谐整定

从图4-4a的异步电动机的T形等效电路表示中可以看出，电动机除了常规的参数如电动机极数、额定功率、额定电流外，还有R_s（定子电阻）、L_s（定子漏感抗）、R_r（转子电阻）、L_r（转子漏感抗）、L_m（互感抗）和I₀（空载电流）。

电动机的参数调谐整定分电动机静止整定和旋转整定2种，其中在静止整定中，变频器能自动测量并计算定子和转子电阻以及相对于基本频率的漏感抗，并同时将测量的参数写入；在旋转整定中，变频器自动测量电动机的互感抗和空载电流。

在调谐整定过程中，必须注意以下几点：

1）调谐过程如果出现过电流或过电压故障，可适当调整价减速时间和转矩补偿数值，并取消故障自动复位功能。

2）在起动调谐前应确保电动机处于停止状态，否则调谐不能正常进行。

3）调谐前必须确保输入电动机的铭牌参数准确无误，否则调谐后的电动机参数不准确。

4）不同品牌不同型号的变频器旋转调谐时从零速加速运行到的频率有些差异，有些是基本运行频率，有些则只有基本运行频率的50%或80%，具体可依据变频器的用户手册。

5）如果现场情况无法对电动机进行调谐的，可以参考同类电动机的已知参数手工输入，或者按照以下方式进行：先选择静止调谐，可依次计算出定子电阻、转子电阻和漏感抗3个参数，不测量电动机的互感抗和空载电流，用户可以根据电动机铭牌自行计算这两个参数，计算中用到的电动机铭牌参数有额定电压U、额定电流I、额定频率f和功率因数η，其中

式中 X_σ代表漏感抗，是定子漏感抗和转子漏感抗之和。

6）为了保证控制性能，必须按变频器标准适配电动机进行电动机配置，若电动机功率与标准适配电动机的功率差距过大（功率差别一般在1～2级之间），变频器的控制将明显下降，或者配用高转差电动机等特殊电动机也将大大影响使用效果。

7）如果在变频器与电动机之间接有电抗器或滤波器等配件的话，将影响到自动调谐的准确度，应该在进行自动调谐前暂时拆除这些配件。