可变频率调速的工作原理

1.异步电动机稳态模型

根据电动机学原理，在下述三个假定条件下（即忽略空间和时间谐波、忽略磁饱和、忽略铁损），异步电动机的稳态模型可以用T形等效电路表示，如图4-4a所示。

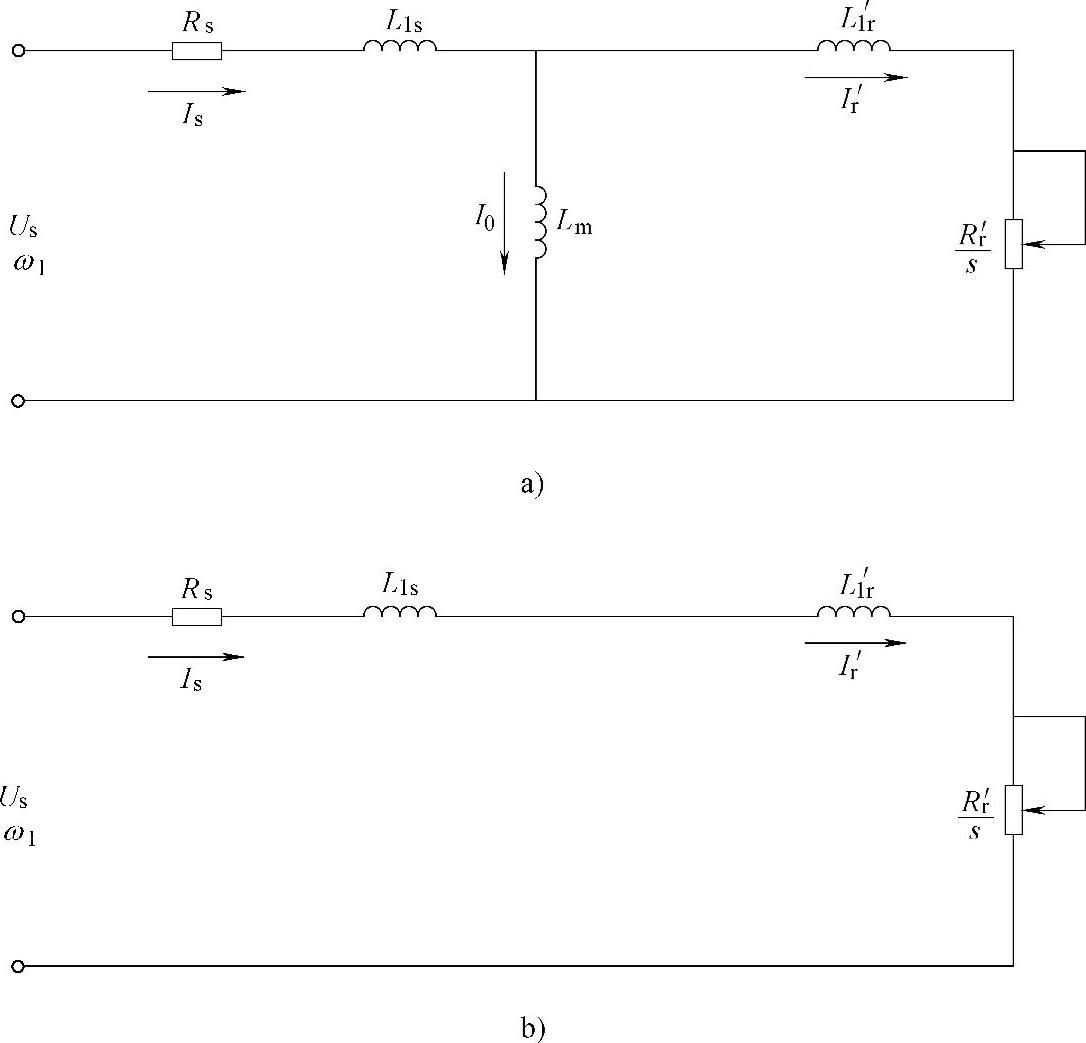
图4-4 异步电动机简化等效电路

a）异步电动机T形等效电路 b）异步电动机简化等效电路

图4-4中的各参数定义如下：

R_s、R_r′——定子每相电阻和折合到定子侧的转子每相电阻；

L_1s、L_1r′——定子每相漏感和折合到定子侧的转子每相漏感抗；

L_m——定子每相绕组产生气隙主磁通的等效电感，即励磁电感；

U_s、ω₁——定子相电压和供电角频率；

I_s、I_r′——定子相电流和折合到定子侧的转子相电流。

根据电动机原理，忽略励磁电流，则得到如图4-4b所示的简化等效电路，并推导出电流公式和每极气隙磁通。

其中电流公式可表示为

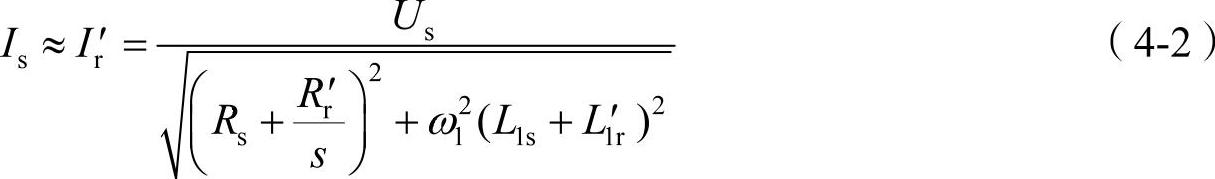
感应电动机的每极气隙磁通为

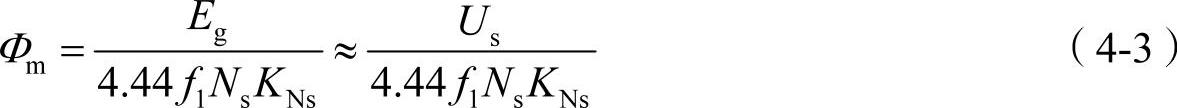(www.xing528.com)

式中 E_g为气隙磁通在定子每相中感应电动势的有效值；f₁为定子频率；N_s为定子每相绕组串联匝数；K_Ns为定子基波绕组系数。忽略定子电阻和漏磁感抗压降，则认为定子相电压U_s=E_g。

2.转速开环的异步电动机变压变频调速

为了达到良好的变频控制效果，常采用电压-频率协调控制（即V/f控制），并分为基频（额定频率）以下和基频以上两种情况。

（1）基频以下调速

以便充分利用电动机铁心，发挥电动机产生转矩的能力，在基频以下采用恒磁通控制方式，要保持Φ_m不变，当频率f₁从额定值f_IN向下调节时，必须同时降低E_g，即采用电动势频率比为恒值的控制方式。然而，绕组中的感应电动势是难以直接控制的，当电动势值较高时，可以忽略定子电阻和漏磁感抗压降，而认为定子相电压U_s≈E_g，则可以从式（4-3）得出如下：

式（4-4）是恒压频比的控制方式，其控制特性如图4-5所示。低频时，U_s和E_g都较小，定子电阻和漏磁感抗压降所占的分量相对较大，可以人为地抬高定子相电压U_s，以便补偿定子压降，称作低频补偿或转矩提升。

（2）基频以上调速

在基频以上调速时，频率从f_IN向上升高，但定子电压U_s却不可能超过额定电压U_sN，只能保持U_s=U_sN不变，这将使磁通与频率成反比地下降，使得电动机工作在弱磁状态。

把基频以下和基频以上两种情况的控制特性画在一起，如图4-6所示。如果电动机在不同转速时所带的负载都能使电流达到额定值，即都能在允许温升下长期运行，则转矩基本上随磁通变化而变化。按照电力拖动原理，在基频以下，磁通恒定，转矩也恒定，属于“恒转矩调速”性质，而在基频以上，转速升高时磁通恒减小，转矩也随着降低，基本上属于“恒功率调速”。

图4-5 恒压频比控制特性

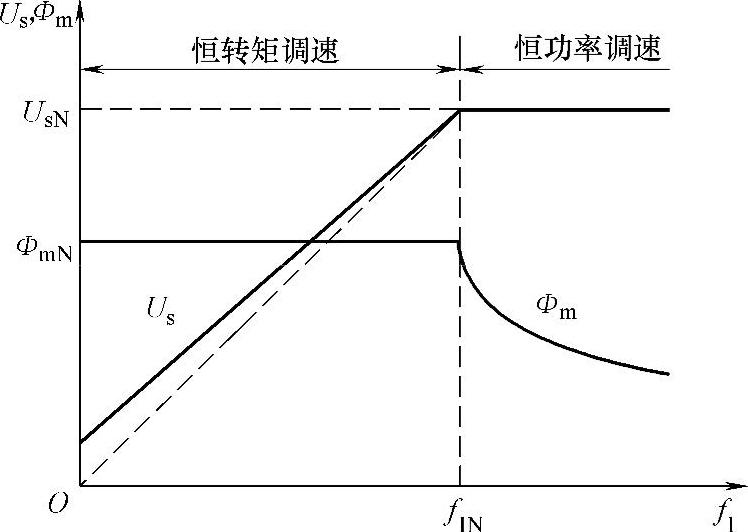
图4-6 感应电动机变压变频调速的控制特性