三相SVPWM与单相SVPWM的比较

2.1 三相SVPWM原理

2.1.1 三相电空间电压矢量分析与dq0变换本质作为对比并方便引出单相空间矢量调制算法，先简要分析三相电空间矢量基

本思想与SVPWM技术基本原理。三相电源线电压是一组互差2π/3的正弦波电压，如式（1）所示。式中

u_AB、u_BC和u_CA为三相电源线电压，U_ϕ为线电压有效值。

取时间t为参变量，式（1）组成三维空间电压矢量u=[u_AB，u_BC，u_CA]^T。当t∈（-∞，+∞）时，矢量u在空间坐标系中形成一个闭合空间电压矢量圆，如图1所示，可以证明，该矢量圆有如下性质；①由u²_AB+u²_BC+u²_CA=3u²_ϕ可知圆半径为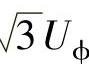；②由u_AB+u_BC+u_CA=0可知矢量u全部落在平面x+y+z=0上。

图1 三相电的空间电压矢量圆

矢量u是以三维线性空间R³的单位标准正交基于（e₁，e₂，e₃），为基底的矢量坐标，其中e₁=[1，0，0]^T，e₂=[0，1，0]^T，e₃=[0，0，1]^T。当t∈（-∞，+∞）时，所有电压矢量u组成R³的线性子空间V_u。可以证明

dimV_u=2 （2）即线性空间V_u是三维线性空间R³的二维线性子空间。如果选择一组新基（y₁，y₂，y₃）做空间坐标旋转变换，且选择其中一个基为线性子空间V_u所在平面单位法向量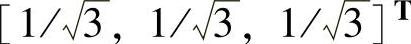时，则该基上的坐标分量将为零（因为该基与V_u正交）；其他两基可取线性子空间V_u所在平面的任意两正交单位矢量。为不一般性，取新基（y₁，y₂，y₃）为

其中，t′∈R为任意常数，y₁⊥y₂⊥y₃为标准正交，那么，由基（e₁，e₂，e₃）到新基（y₁，y₂，y₃）的过渡矩阵C为

（y₁，y₂，y₃）=（e₁，e₂，e₃）C （4）

则原空间电压矢量u在新基下的坐标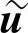为

特别地，当ωt′=π/2时

即通过将原坐标轴（e₁，e₂，e₃）旋转至新坐标轴（y₁，y₂，y₃）的坐标旋转变换，则原三相空间电压矢量圆被映射到dq0坐标系平面圆上，且圆半径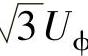不变。另外，从式（9）可知，工程计算中常用的dq0变换只是众多（无穷个）三相空间电压矢量基变换过渡矩阵式（5）逆变在ωt/=π/2时的特例。

2.1.2 三相逆变电源空间电压矢量分析

典型三相PWM逆变桥电路如图2所示，可能产生的8种离散线电压矢量如式（11）所示。

其中，V_dc为逆变桥母线电压；v_xy=v_x-v_y（x，y=a，b，c）为逆变桥输出线电压；a，b，c为三相逆变桥各臂开关状态，非0即1，其中1表示该桥臂上面开关导通，下面开关截止；0则相反。

图2 三相PWM逆变桥电路

矢量v=[v_ab，v_bc，v_ca]^T在空间形成8个离散电压矢量，其中两个为零电压矢量。同样，通过坐标旋转变换[见式（6）]可将这8个离散电压矢量映射至平面电压矢量，如式（12）所示。

其中，V_dc与a，b，c同上。

形成的8个离散平面电压矢量如图3所示，图中电压矢量所形成正六边形的内切圆半径为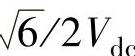，与式（10）电压矢量圆半径的比值构成逆变系统输出的电压调制比，如式（13）所示。

图3 坐标变换后的8个电压矢量图

由式（13）可知，直流母线电压V_dc的大小决定了逆变系统输出线电压的峰值。利用这8个离散电压矢量的线性组合来逼迫期望输出电压矢量即为三相SVPWM的基本思想。(www.xing528.com)

2.2 单相SVPWM原理

2.2.1 单相电源电压矢量空间与坐标旋转变换

单相电源与三相电源有着本质的不同，不能简单的同三相电源一样能进行空间电压矢量分析，用参考式（1）引入单相正弦电源的线电压形式，

取t为参变量，式（14）组成单相空间电压变量u=[u_AB，u_BA]^T。当t∈（-∞，+∞）时，矢量u在平面坐标系中形成平面电压矢量，如图4所示。

与三相空间电压矢量相似，因为u_AB+u_BA的单相空间电压矢量u全部落在平面直线x+y=0上，可以证明，所有矢量u组成的矢量空间V_u是R²一维线性子空间。因此，参考三相的三维空间坐标旋转变换，取图4中α、β轴正方向上的单位矢量两新基（y₁，y₂）

图4 单相正弦电的平面电压矢量图

其中，基y₂为V_u所在直线单位法向量。显然，基下y₂轴上的坐标分量将为零。由（e₁，e₂）到新基（y₁，y₂）的过渡矩阵C为

（y₁，y₂）=（e₁，e₂）C （16）

那么，原空间电压矢量u在新基下的坐标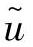为

如图5所示。

2.2.2 单相逆变电源空间电压矢量分析

典型单相PWM逆变桥电路如图6所示，产生四种离散输出线电压矢量，见表1。其中，“0”表示关断；“1”表示开通。

图5 坐标旋转变换后的单相电压矢量图

图6 单相PWM逆变桥电路

表1 单相逆变器的4种开关状态

用矩阵表示，如式（20）所示。

电压矢量v=[v_ab，v_ba]^T在空间形成4个离散的电压矢量如图7所示。同理，取新基式（15）对式（20）的坐标旋转变换，可得

图7 单相逆变桥输出电压矢量图

图8 坐标变换后的4个电压矢量图

变换后的电压矢量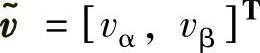如图8所示。同理，可以定义期望同电压矢量模与逆变输出电压矢量模的比值为单相逆变系统的电压调制比，如图（22）所示。