简化多电平SVPWM算法二例

（1）用参考电压矢量所在三角形算法^[4]

由于任意一个多电平逆变器的参考电压矢量，均处于电压矢量分布图中一个三角形中如图6-14所示。为了利用电压矢量u₁（α₁，β₁），u₂（α₂，β₂）以及u₃（α₃，β₃）合成参考电压矢量u₀（α₀，β₀），u₀即前述的u_ref有如下表达式：

u₀=d₁u₁+d₂u₂+d₃u₃（d₁+d₂+d₃=1） （6-15）

式中 d₁、d₂及d₃——矢量u₁、u₂和u₃作用占空比。

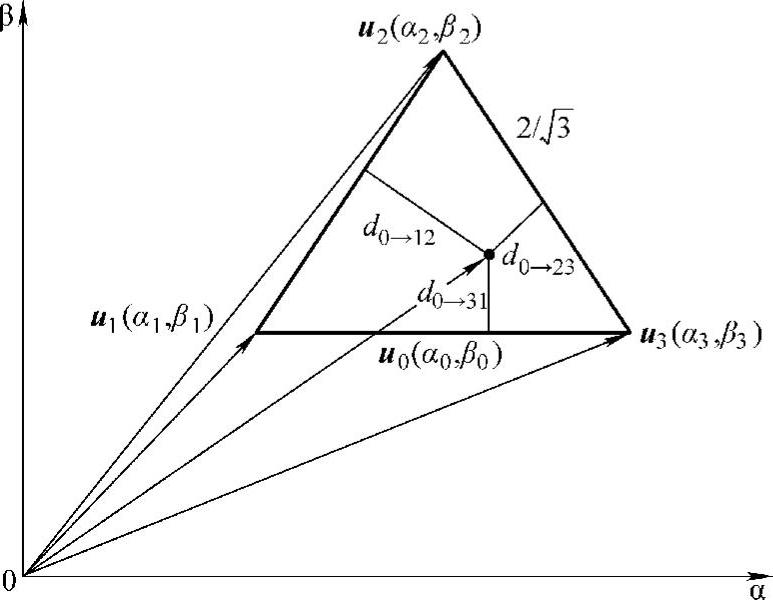
图6-14 多电平逆变器矢量合成的基础

若任意3个矢量顶点构成的正三角形均全等，且三角形边长均为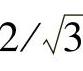，这样三角形的高为1，则式（6-15）占空比计算公式简化为下式所示：

d₁=d_0→23，d₂=d_0→31，d₃=d_0→12

在三相变换器的矢量图中，所有的三角形均为正三角形，且均全等。但要使式（6-15）适用，我们在做坐标变换时，要选择一个合适的系数，使得三角形的边长为2/3。采用线电压坐标系，这样任何一个三角形的三个边分别垂直于轴ab、bc和ca。这样从参考矢量端点到一个三角形的边距离等于参考矢量在三个坐标轴上的投影。

以下即为本算法计算步骤：

第一步：获得参考电压矢量及其投影。

根据控制算法，计算出αβ定子静止两相坐标系中定子电压参考矢量分量u_sα^*和u_sβ^*，并把它的坐标变换到abc三相坐标系中，得三个轴线上的分量u_a^*、u_b^*、u_c^*为

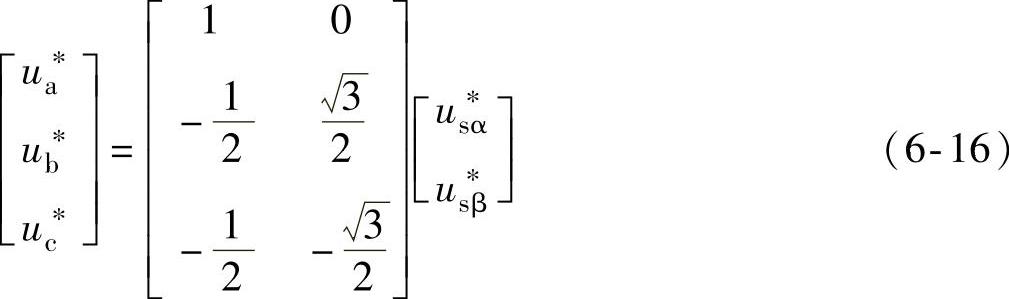
把式（6-16）所示的三相坐标系中的相绕组量变换到ab、bc及ca三相线电压坐标系中，且为了使得每个三角形边长为2/3，取缩小系数为（m-1）/U_DC，得

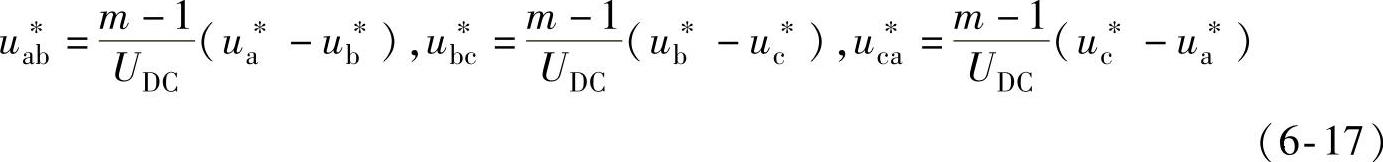
式中 m——逆变器电平数。

经坐标变换后的坐标系及电压矢量如图6-15所示。

第二步：对投影取整。

令floor（x）为不大于变量x的最大整数；ceil（x）为不小于变量x的最小整数，则对轴ab、bc、ca上的投影分量分别取整得

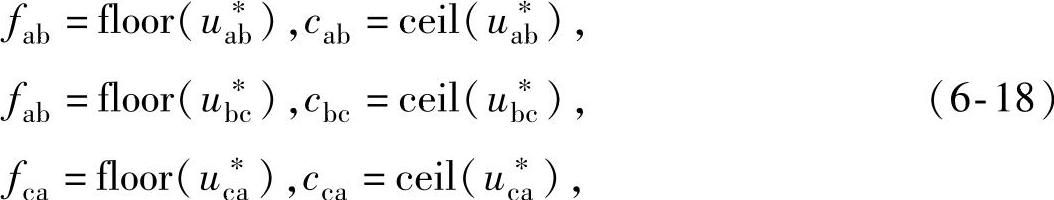
注意f_ab+f_bc+f_ca≠0，c_ab+c_bc+c_ca≠0。

第三步：确定最近的三个矢量及计算各自的占空比。

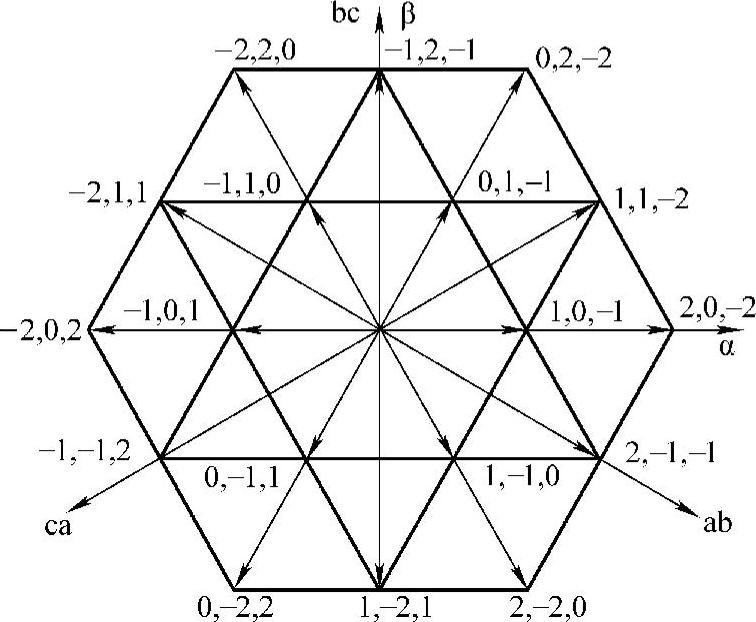
图6-15 经坐标变换后的坐标系及电压矢量

利用前面求得的投影分量的整数，参考电压矢量所处的三角形及用于合成该参考电压矢量的三个最近电压矢量，可方便地确定出。f_ab+f_bc+f_ca=-1时，最近的三个电压矢量及其占空比如下：

式中 u_ffc——由f_ab、f_bc及c_ca定义的矢量；

u_cff——由c_ab，f_bc及f_ca定义的矢量；

u_fcf——由f_ab、c_bc及f_ca定义的矢量；

d_ffc、d_cff、d_fcf——矢量u_ffc，u_cff，u_fcf作用的占空比。

如果f_ab+f_bc+f_ca≠-1，最近的三个电压矢量及其占空比如下：

上述两种三角形定义如图6-16所示。

第四步：把矢量映射成开关状态。

该SVM算法最大的优点在于它能直接把所选择的电压矢量映射成多电平三相逆变器的开关状态。

这里，以参考矢量u_fcf为例。设线电压坐标系中开关矢量为（a，b，c）对应坐标变换前的开关矢量为（S_a，S_b，S_c），则

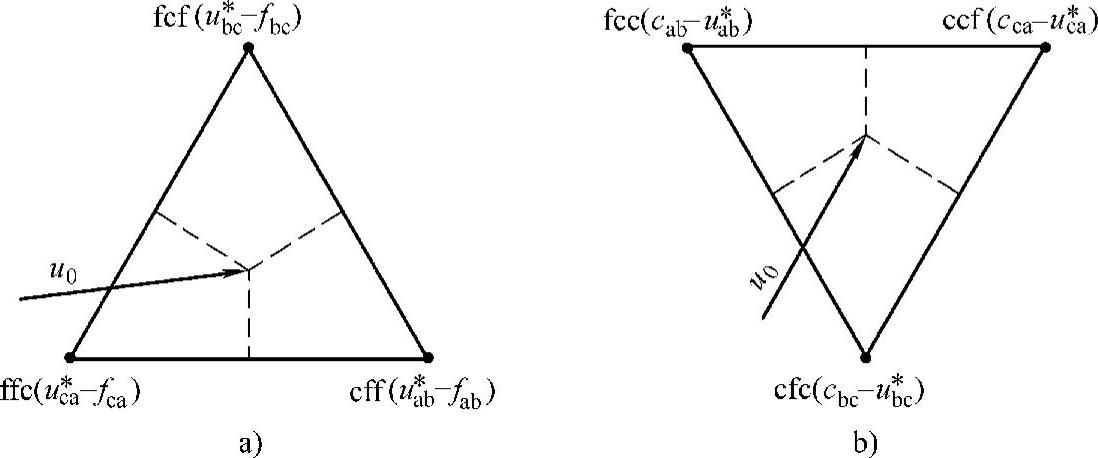
图6-16 多电平逆变器矢量及其占空比

a）f_ab+f_bc+f_ca=-1 b）f_ab+f_bc+f_ca≠-1

（2）用新m、n坐标系算法^[5](www.xing528.com)

本方法用一种坐标系，将三电平电压矢量分布图中一个三角形用坐标m、n来表示。

因为对称性，下面仅针对区域Ⅰ进行分析，整个处理过程总共由4个步骤组成。

步骤一：对基本空间电压矢量的预处理。

图6-17示出图6-15中的区域Ⅰ，在图中新的坐标系m，n被用来描述电压矢量。和一般的直角坐标系不同，这里的m，n坐标系的两个坐标轴之间成π/3角度，并且只需要考虑第一象限内的情况，因为当U_r落在其他几个区间的时候，只需要将坐标系分别顺时针旋转一个角度kπ/3（k=1，2，3，4，5分别对应区域Ⅱ、Ⅲ、Ⅳ、Ⅴ、Ⅺ）。在新的坐标系中，原来的空间电压矢量可用坐标来表示，其中坐标为整数的点对应基本电压矢量。

图6-18示出U_r的分解示意图。在一般情形下，对于一个（M+1）电平逆变器，U_r可表示为U_rm，U_rn，并容易计算得到：

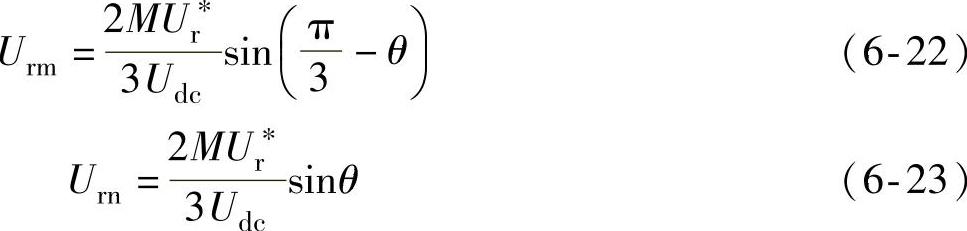
式中 U_r^*——矢量U_r的幅度。

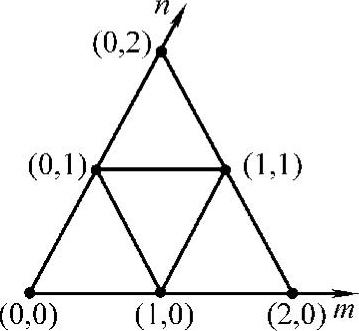
图6-17 用m，n坐标表示

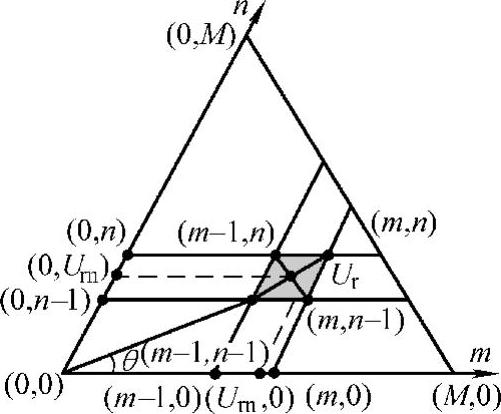
图6-18 参考电压矢量的分解示意图

U_r^*和其他坐标的关系可由余弦定理得到：

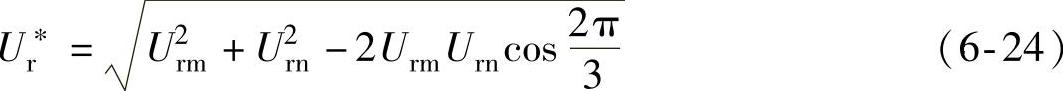
步骤二：选择邻近的3个基本电压矢量。

设参考电压矢量满足以下不等式（参见图6-18）：

m-1＜U_rm＜m （6-25）

n-1＜U_rn＜n （6-26）

式中 m，n——整数。

有3种情况：

a）U_rm+U_rn＜m+n-1这意味着U_r位于左下用阴影表示的三角形中，这时（m-1，n-1），（m-1，n）和（m，n-1）为应该被选的3个基本电压矢量；

b）U_rm+U_rn＞m+n-1这时U_r位于右上的用阴影表示的三角形中，这时（m-1，n），（m，n-1）和（m，n）来合成U_r；

c）U_rm+U_rn=m+n-1这时U_r位于两个三角形的公共边上，①或②情况选择的基本电压矢量均适用；

步骤三：计算被选择的基本矢量的作用时间。

设由步骤二选择好的3个邻近的基本矢量为（m₁，n₁）、（m₂，n₂）和（m₃，n₃），它们对应的作用时间分别为t₁，t₂和t₃。通过解方程组得到的3个基本电压矢量的作用时间分别表示为

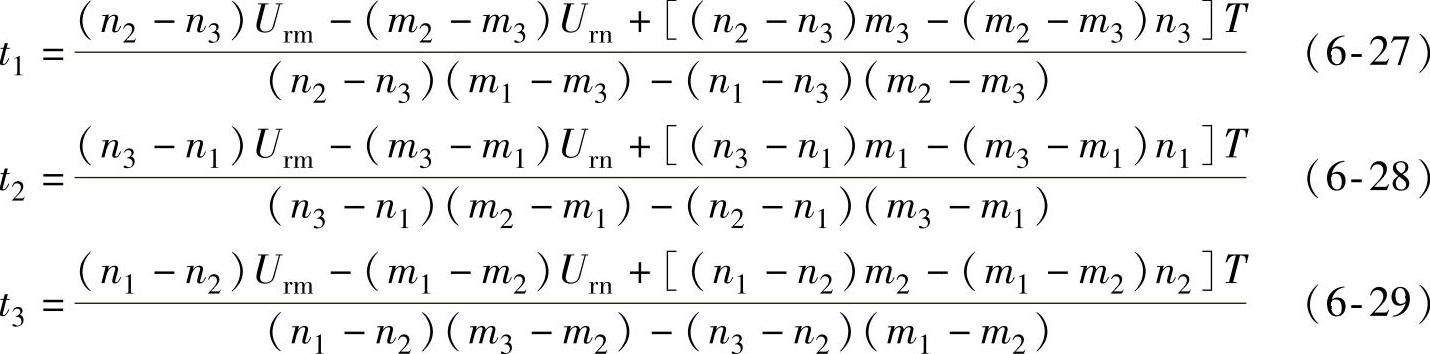
因为m₁，m₂和m₃相互之间相差0或1，n₁，n₂和n₃相互之间也相差0或1，因此式（6-27）～式（6-29）的计算量很小。

步骤四：中点电位平衡控制。

在多电平逆变器的控制中中点电位的平衡非常重要的，下面给出两种保持中点电位平衡的方法：

①合理选择脉冲序列。当U_r落在由U₁，U₂和U₈为顶点组成的三角形中的时候，开关状态可以为POO-PON-OON-ONN或者PPO-POO-PON-OON两种。这两种开关序列可以产生同样的输出电平，但它们对中点电位有相反的作用；

②根据中点电位情况重新分配冗余电压矢量的作用时间。

在本文的仿真和实验中采用方式①。过调制时U_r位于六边形的外部，使得输出电压波形产生较大畸变。当出现过调制模式时，需对步骤①进行处理：首先，通过的下式判断SVPWM是否处于过调制状态：

U_rm+U_rn＞M （6-30）

如图6-19所示，用U_r′代替U_r是一种比较常用的过调制处理方式。U_r′、U_rm′和U_r′_n的幅度可通过在它们对应的原始值上乘以一个系数M/（U_rm+U_rn）得到。经过这样处理后，其他步骤与一般情况下SVPWM的实现步骤是一样的。本算法的仿真和实验波形如图6-20所示，可见效果很好。

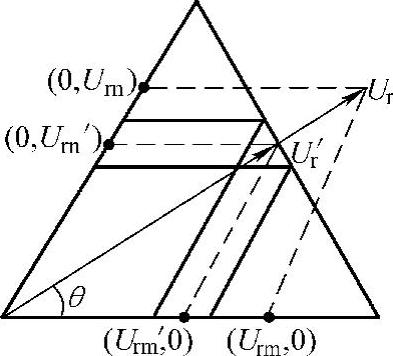
图6-19 过调制模式

简化算法极具优越性。同时该算法的复杂程度并不会随着电平数的增加而增加，因此适用于电平数比较高的应用场合，因此特别适用于级联型逆变器。

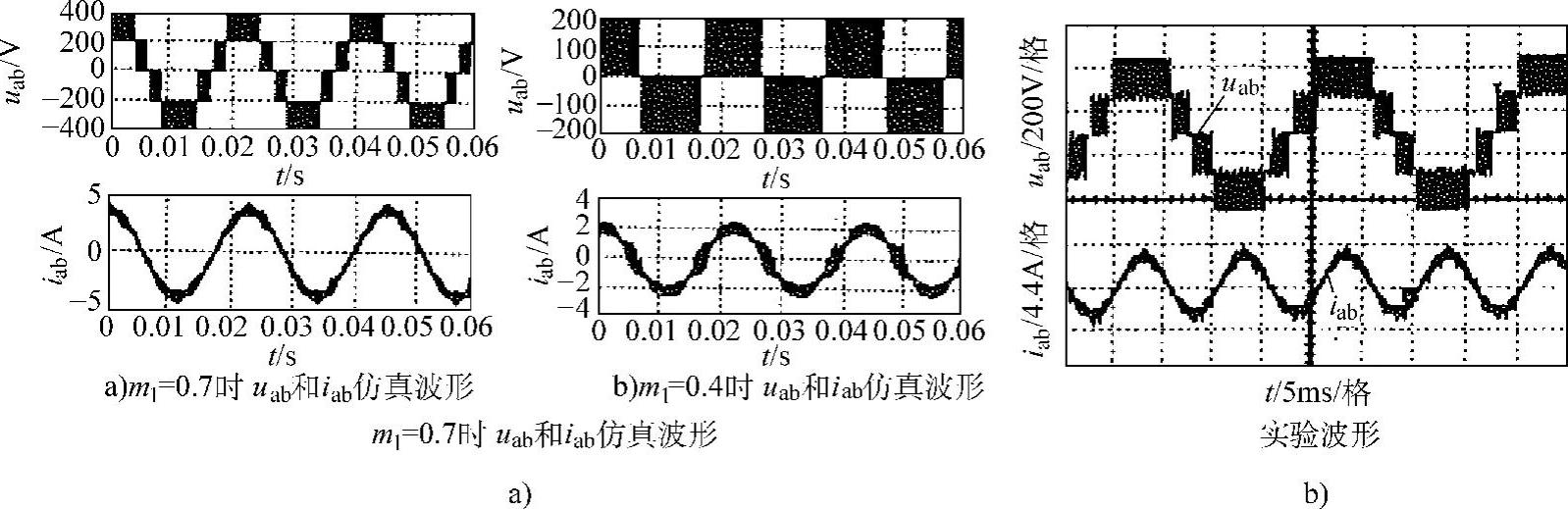
图6-20 仿真和实验波形

a）仿真波形 b）实验波形