各类坐标系算法详解

（1）传统的笛卡儿α-β坐标系算法^[1]

此法类似于三电平SVPWM简化为两电平算法。由于普通两电平SVPWM算法比较简单，如果能将多电平空间矢量分为两电平的空间矢量的组合，如图6-11所示，将使得SVPWM算法大为简化。

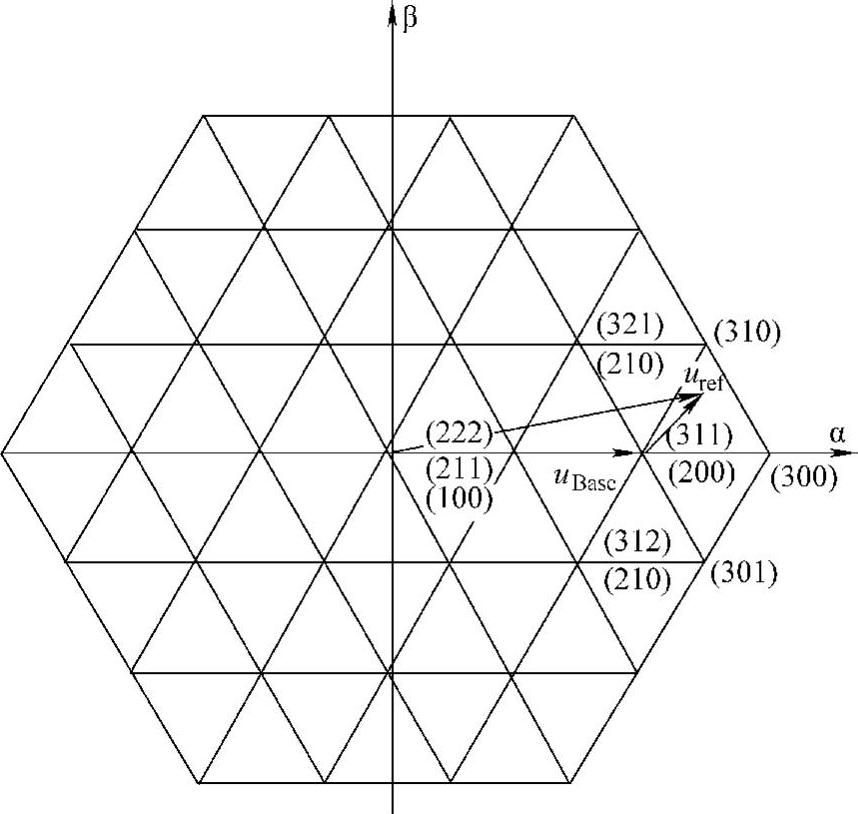
图6-11 参考矢量的分解

此方法是在多电平空间矢量图中，将参考电压矢量分解成为基矢量和两电平分矢量，然后用类似两电平空间矢量的方法确定构成小三角形三个顶点的基本矢量，以及计算对应的作用时间。

根据上述思想，对任意多电平三相参考电压可以分解为基矢量和对应两电平分量的矢量和，可表示为

u_ref=u_rBase+u_r′ （6-4）

式中 u_ref——多电平逆变器给定参考电压矢量；

u_rBase——基矢量；

u_r′——等效两电平空间矢量。

根据伏秒平衡的原则，多电平逆变器的三个基本矢量合成参考电压矢量的公式表示为

U_ref·Ts=U₁·T₁+U₂·T₂+U₃·T₃ （6-5）

不计零序分量，对三相参考电压的整数分量和两电平分量进行Clark变换，表示为笛卡儿αβ坐标系中的空间矢量形式，得到αβ坐标系中的基矢量和两电平分矢量：

参考电压基矢量为

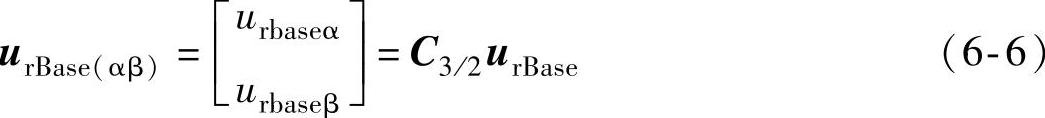
两电平分矢量为

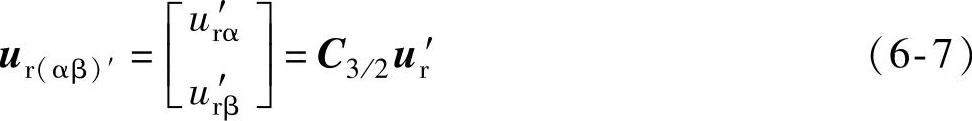
于是αβ坐标系下的电压参考矢量u_ref（αβ）如下式表达：

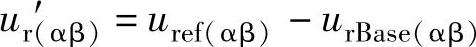
基本矢量如下式：

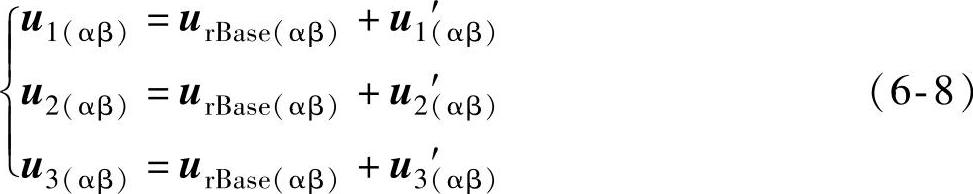
伏秒特性为

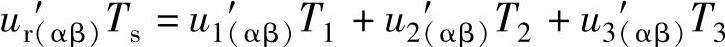
或

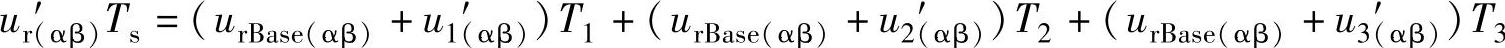
基本矢量工作时间如下式：

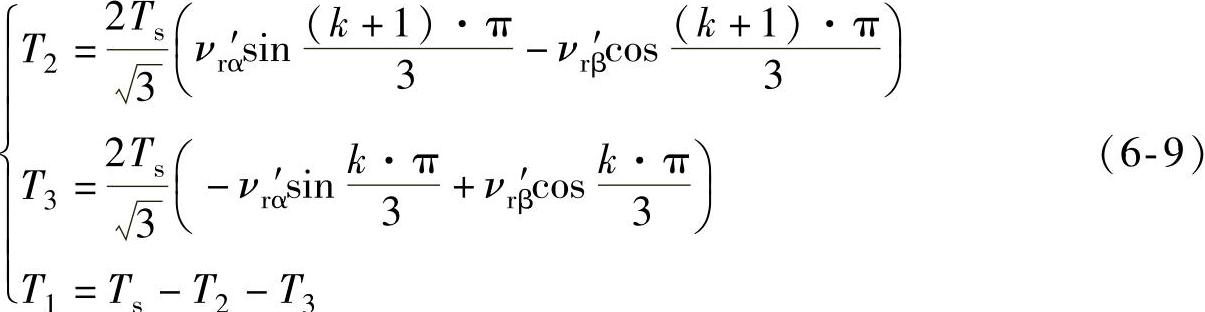
式中 T_s——开关周期。

通过上述计算，便可得出合成参考矢量的三个基本矢量及其作用时间。

（2）60°坐标系多电平算法(www.xing528.com)

上一节讲述的αβ坐标系多电平控制算法，虽然做到简化，提出也最早，但仍显得计算量大，因此许多学者进行简化的探索，提出了许多新的算法方案，60°坐标法是较为成熟的一种。

这种控制策略是通过坐标变换将ABC三相坐标变换为非正交的60°（g，h）坐标系。即是将传统的三电平空间电压矢量坐标转化为描述一个三维空间线电压矢量u_ref=[u_abu_bcu_ca]^T。因此，60°（g，h）坐标变换下的参考矢量可以表示为u_ref（g，h）=Tu_ref（u_ab，u_bc，u_ca）。其中变换矩阵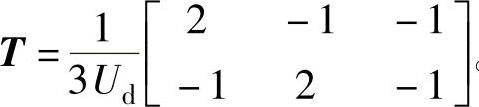。通过对参考矢量的坐标进行向上、向下取整，可得在新坐标系下合成参考矢量的3个（g，h）坐标；根据幅秒平衡原理，可求得3个坐标的作用时间；最后通过坐标变换，将得到的3个（g，h）坐标反变换为ABC三相标系下的空间矢量。

详细推导过程可参考第4章。

（3）KL坐标系SVPWM算法^[7]

此种多电平SVPWM算法采用KL坐标系，如图6-12a所示。在该坐标系中，L轴与α轴重合，K轴是β轴逆时针旋转30°形成的，可见K轴与B相重合。当逆变器输出状态形成的u_r落在图6-12b所示的某一个三角形内。则u_r将由这三角形顶点u₁、u₂、u₃3个矢量合成。

图6-12 KL坐标系多电平逆变器空间矢量图

按图6-12a示出KL坐标系下的空间矢量示意图，可得到图6-12b KL坐标系下空间矢量合成图，参考矢量u_ref落在k_n、k_n+1、l_m、l_m+1构成的菱形区内。这个菱形内部包含两个三角形。将上面的三角形称之为Ⅰ型，下面的三角形称之为Ⅱ型。

1）假如u_r落入三角形Ⅰ型内部，它将由矢量u_m，n、u_m，n+1、u_m+1，n+1合成，可得到作用时间为

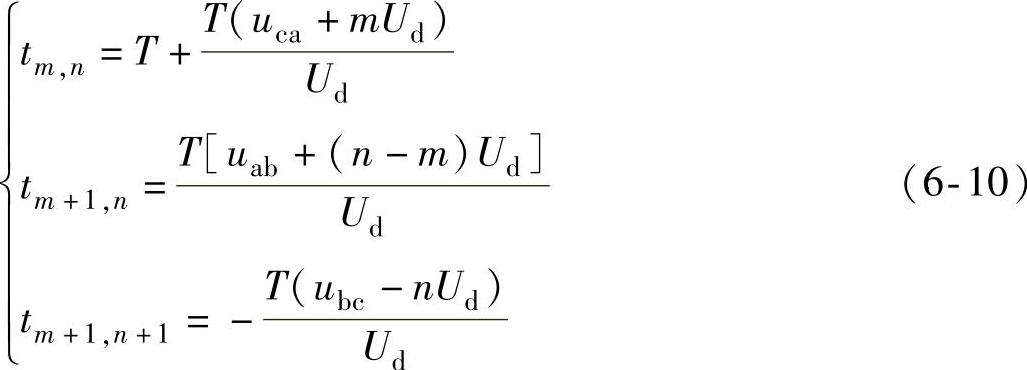
2）如果U_r落入三角形Ⅱ型内部，U_r将由u_m，n，u_m+1，n，u_m+1，n+1合成，可求得

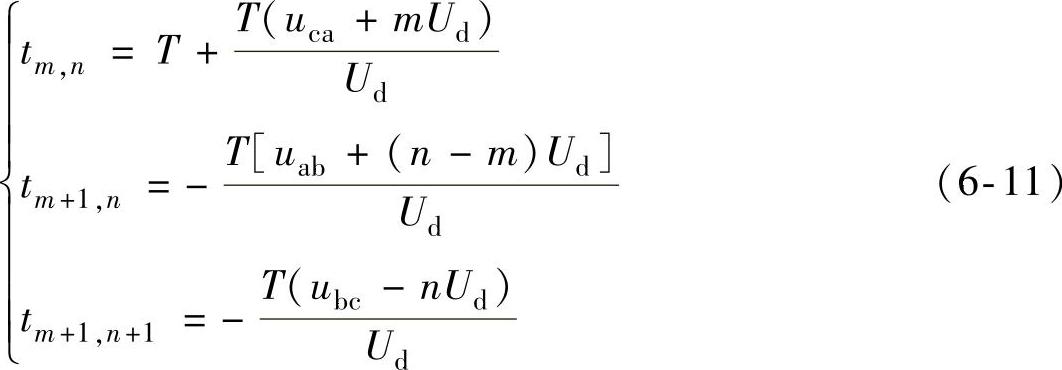
式（6-10）和式（6-11）为合成3个矢量持续时间，可见整个算法只包含简单的乘法、加法运算，十分简便，因此，若用KL坐标系算法解决电网电压缺损的问题，可以取得良好的效果^[7]。

（4）ja-jb-jc虚坐标法^[1]

本算法采用二维坐标系，如图6-13中所示的ja-jb-jc坐标系，其中的ja轴即为αβ坐标系下的β轴，而jb、jc轴也就可以看作b相和c相逆时针旋转90°后对应的虚轴。因此把这种三轴坐标系称为虚坐标系。

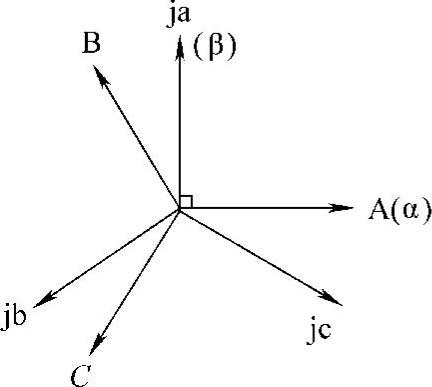
图6-13 平面上的三轴坐标系

设x_ja，x_jb，x_jc和x_a，x_b，x_c分别为ja-jb-jc虚坐标系和ABC坐标系下的值，则ABC坐标系到ja-jb-jc虚坐标系的转换关系如下式所示：

而从αβ坐标系到ABC坐标系的反Clark变换为如下式所示：

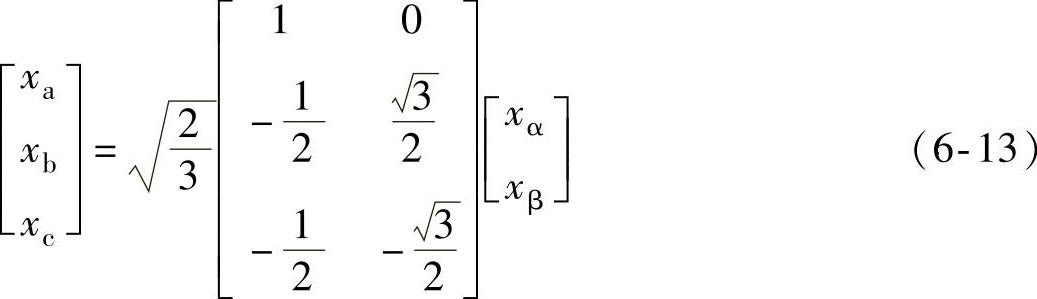
其中，x_α，x_β为αβ坐标下的值，则由式（6-12）和式（6-13）可以得到从αβ坐标系到ja-jb-jc坐标系的变换，即

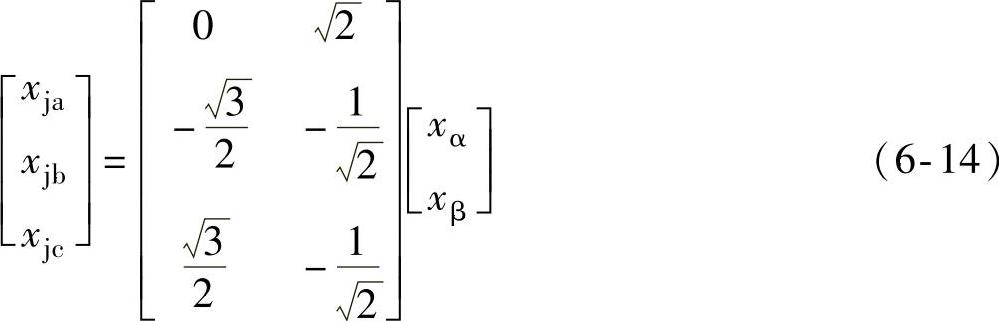
由此可见，采用ja、jb、jc三个坐标轴表示一个二维矢量，一方面体现了三相对称的特点，便于数学分析；另一方面，变换后的三个坐标值分别是输出的三个线电压，物理意义明确。

1）非零序分量的控制。这一部分的任务是在根据参考矢量u_ref确定合成矢量的坐标和对应作用时间。参考矢量一般选择与参考矢量最近的三个基本矢量来合成，即其终点所在小三角形的三个顶点。其步骤：第一步由参考矢量终点坐标值确定所在的三个顶点的坐标值，第二步计算三个顶点对应的作用时间，即占空比。

2）零序分量的控制。当三个基本矢量确定后，每个矢量通常对应几个不同的开关状态。定义一个采样周期内顺序输出的开关状态为输出开关序列，则三个矢量的全部冗余开关状态可以组成若干组输出开关序列，每一组序列对应不同的零序分量输出，通过选择不同的开关序列，就可实现不同的零序目标。因此，多电平逆变器零序分量控制实际是在只影响输出零序分量的条件下变换开关状态组合。实现这一控制步骤包括冗余开关状态的确定、输出开关序列形式的确定以及计算每相的占空比。

同零序分量和三相输出开关序列之间的关系。

虚坐标系算法突出的特点是考虑了零序分量的控制，这是当前研究的热门课题，整个详细内容请参阅参考文献[1]。