多电平逆变器的空间电压矢量分布与优化

由于目前采用SVPWM技术主要是二极管钳位式逆变器，所以下面讲述空间矢量分布、参考矢量的位置、基本矢量选择、开关作用时间计算、开关状态输出模式的确定等SVPWM算法，主要是结合这类逆变器，但其他类型的多电平逆变器，只要是相同电平数逆变器也可以适用。

图6-8所示为三相多电平逆变器的开关模型，电路是一个三相电压源，这个电压源的每一相可以输出多级的直流电平，对于一个n电平逆变器，假设每一级的电平值为

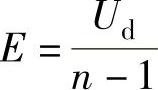
则每相可以输出0、E、2E、…、（n-1）E，共n种不同的电平值，图6-8即为典型的带三相对称负载的多电平逆变器开关模型。

设图6-8中三相的开关函数为S_a、S_b、S_c，S_a，b，c={0，1，K，n-1}，则三相输出可分别表示为u_a=S_aE，u_b=S_bE，u_c=S_cE。以逆变器直流侧最低电位为参考零点o，则每一相输出的电平序数可以表示为0，1，K，（n-1）。设负载的中点为N，则输出电压用以下方程式表示：

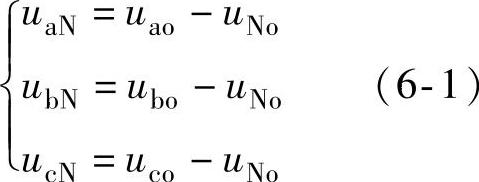
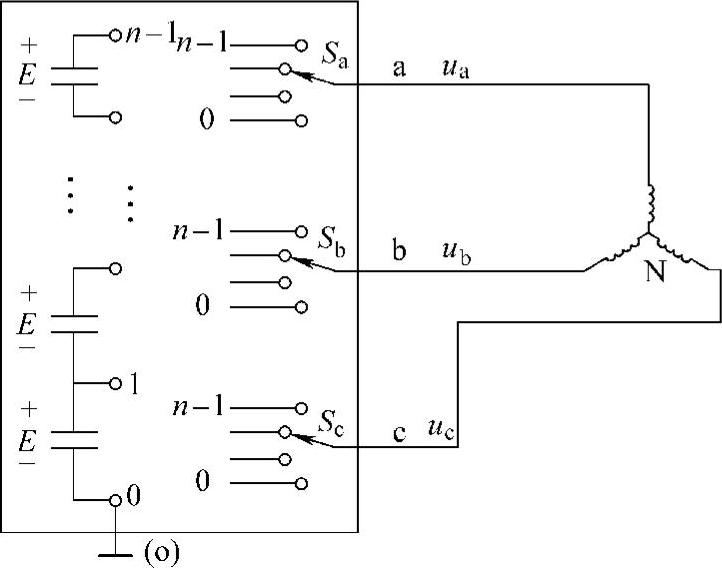
图6-8 带三相对称负载的多电平逆变器 带三相对称负载的开关模型

三相负载平衡时，负载相电压之和为零，将式（6-1）各式相加得到式（6-2）：

式中 u_aN，u_bN，u_cN——负载相电压；

u_ao，u_bo，u_co——逆变器三相输出电压；

u_No——负载中点对逆变器零参考点的电压。

若三相不平衡，u_No为逆变器输出的零序分量。对于三相多电平逆变器的输出电压，与前述三电平一样，空间矢量可定义为(www.xing528.com)

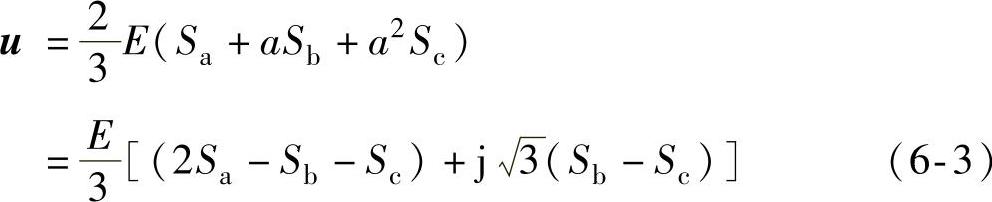
式中 ；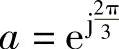

E^*=（n-1）E。

多电平逆变器空间状态矢量有如下特点：

1）三相多电平逆变器有n³种输出开关状态，即有n³个空间矢量。

2）共有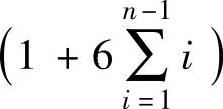个基本矢量（有效矢量）。

图6-9所示为四电平逆变器空间矢量和开关状态图，图中示出了基本矢量，可看到内部冗余矢量逐层增加，每深入一层增加一个。

根据开关逻辑分析，可知随着电平数的增多，多电平基本矢量和相应的开关状态冗余进一步增多，同时多电平运行状态控制的复杂程度也大大增加，使得多电平SVPWM算法也越来越复杂，其性能要求也更高。

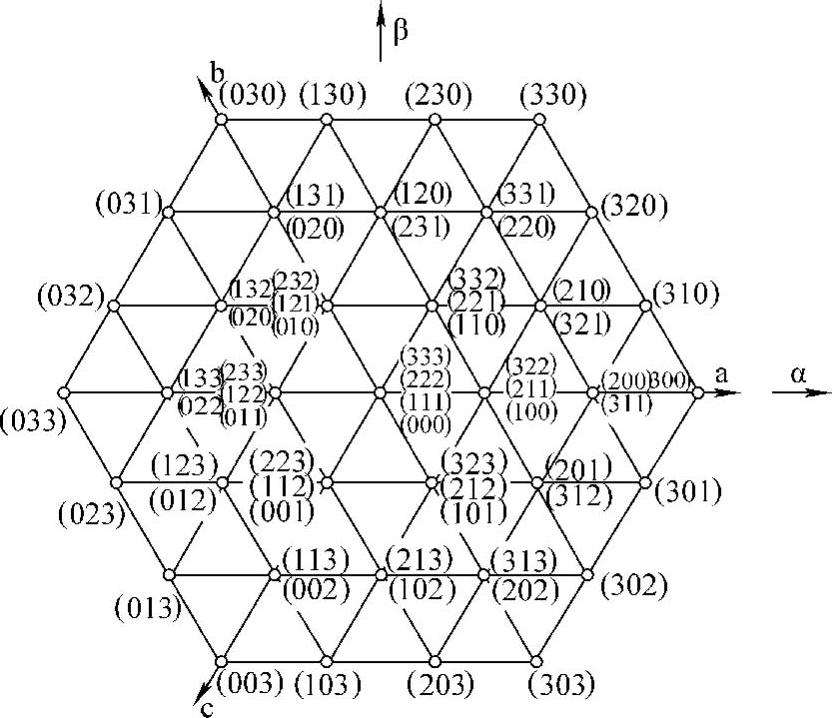
图6-9 四电平逆变器空间矢量和开关状态

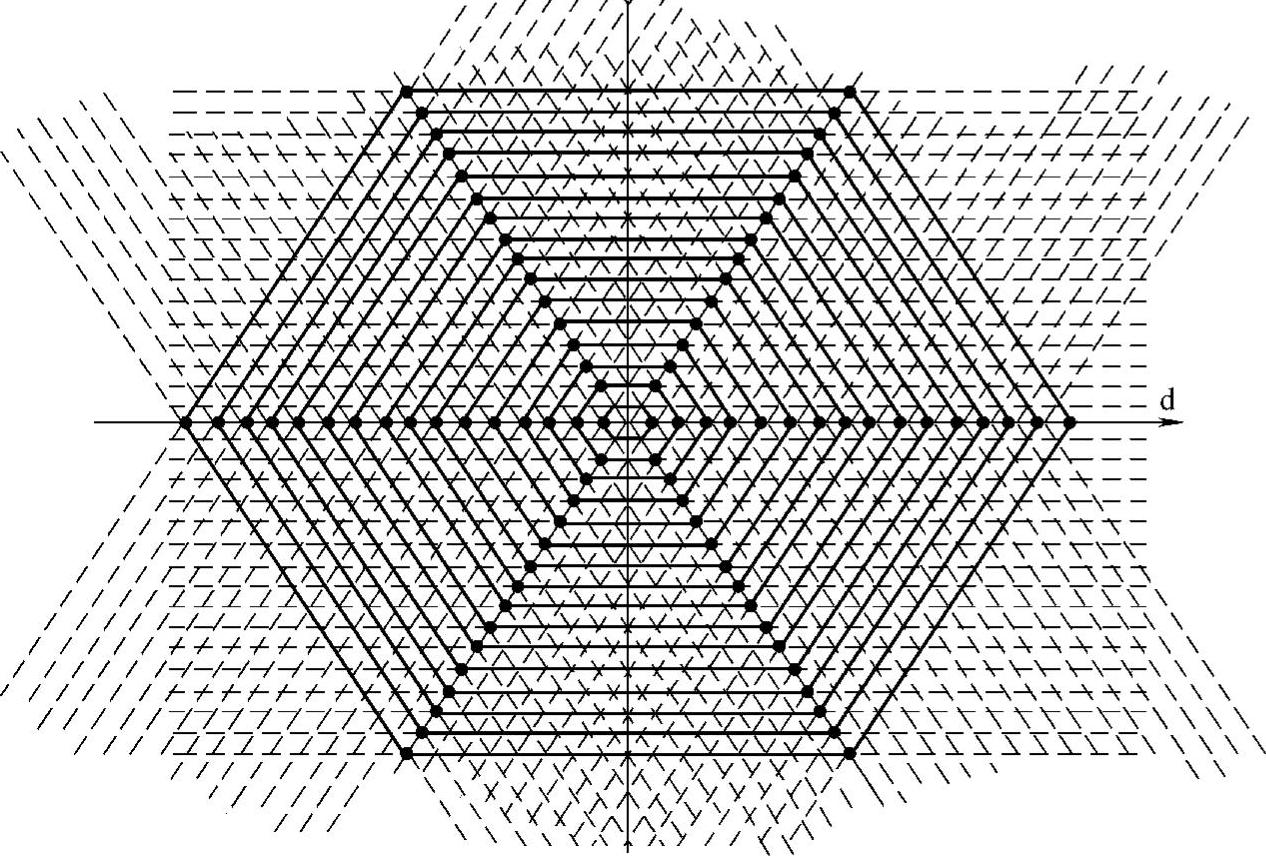
图6-10 8单元17电平的空间矢量

功率单元串联式逆变器中的8单元逆变器为17电平。图6-10所示为8单元17电平的空间矢量图。如果任一相要有0～8个输出电平，可组合256种空间电压矢量，那么三相就有它的立方数，即16777216个空间矢量，它们分别落在图中所示的大六边形内部的各个交点上，其控制算法将十分复杂。