260°坐标系SVPWM算法解析

本算法的基本思路是，鉴于图4-7中三电平基本空间矢量之间的角度均为60°的倍数这一几何特性，可以采用非正交的60°坐标系。这样一来会有助于简化参考矢量的合成和作用时间的计算，计算量减少，便于对三电平NPC逆变器实现快速脉宽调制控制。

为了计算方便，在本方案中，逆变器输出电平不采用P、O、N标记，而用2、1、0分别代替P、O、N。

1.60°坐标系

设采用的60°坐标系为gh坐标系，取g轴和αβ坐标中α轴重合，逆时针转60°为h轴，如图4-12所示。

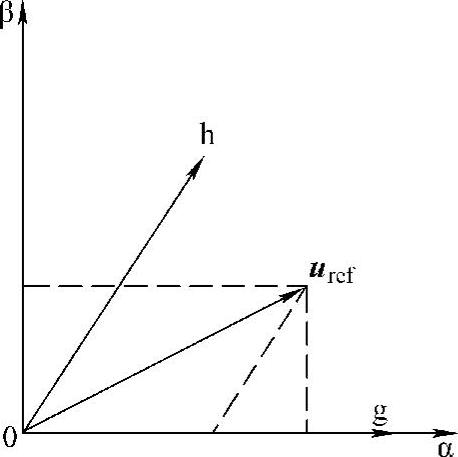
图4-12 gh坐标系与αβ坐标系

设参考矢量u_ref在αβ坐标系下的坐标为（u_rα，urβ），变换到gh坐标系下的坐标为（u_rg，urh），根据线性关系可得到两种坐标系的变换为下式：

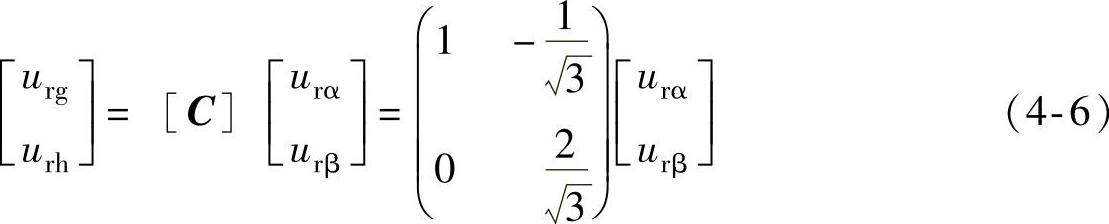
当以ABC坐标形式表示时，设三相电压为u（u_a，u_b，u_c），则由Clark变换可以得到在gh坐标系下的电压矢量形式，其变换如下式所示：

将三电平逆变器的基本矢量变换到gh坐标系下，得到变换到60°坐标系下的三电平空间矢量图，如图4-13所示。

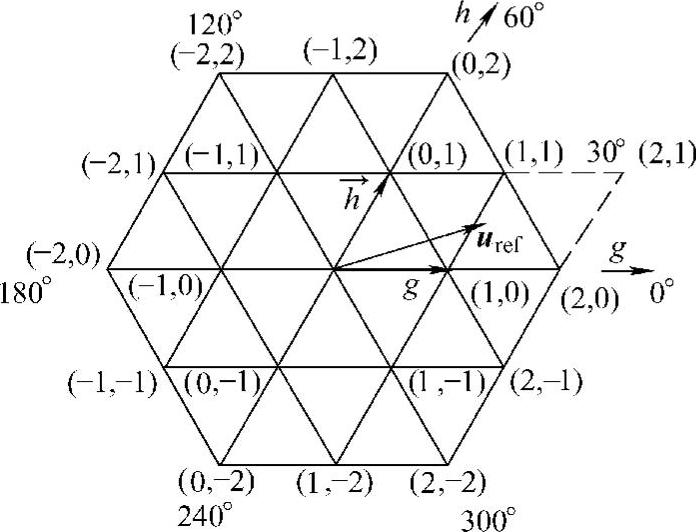
图4-13 60°坐标系下三电平空间矢量图

2.选择基本矢量

由图4-13可知，所有的基本矢量的坐标为整数，因此对于任意的空间参考矢量u_ref（u_rg，u_rh），距离其最近的4个电压矢量可以由空间参考矢量的坐标的向上和向下取整得到。对于如图4-13的参考矢量，对应的4个电压矢量设为

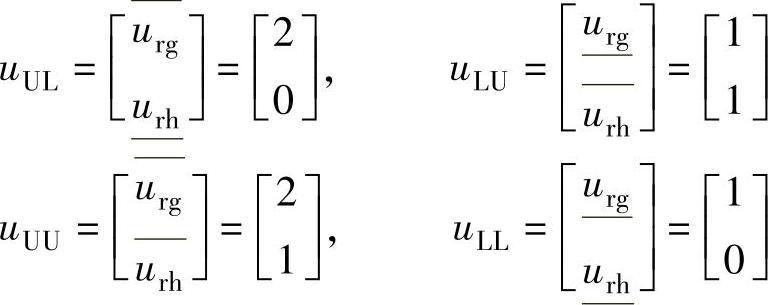
上式中，在坐标变量上画线表示向上或向下取整，且矢量下标U代表其中的变量向上取整，L代表向下取整。这4个矢量的终点构成一个等边平行四边形，此等边平行四边形被由u_UL/u_LU终点构成的对角线分成两个等边三角形。同时u_UL/u_LU总是两个最近的矢量。那么第三个矢量就是剩下的两个矢量中的一个，这个矢量必然与参考矢量落在由u_UL/u_LU的终点所构成的对角线的同一侧，此对角线为(https://www.xing528.com)

g+h=u_ULg+u_ULh （4-8）

因此根据表达式u_rg+u_rh-（u_ULg+u_ULh）的符号，我们便可以判断第三个矢量，即当表达式的值大于零，u_UU是第三个矢量，当表达式的值小于等于零，则u_LL是所要求得的第三个最近的矢量。以图4-13为例，求得的三个最近的矢量为

3.计算作用时间

当三个最近的矢量被确定，则可以通过下面的方程组的求解得出各个矢量的占空比：

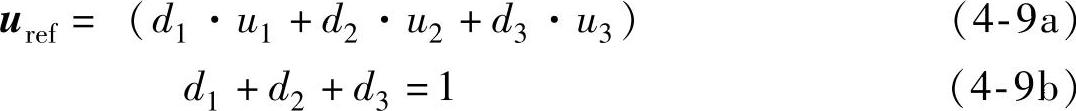
其中，u₁=u_UL，u2=uLU，u3=uLL或u3=uUU。所有的开关状态的坐标为整数，方程组的解可以基于参考电压的小数部分而获得。

1）当u₃=u_LL时，将式（4-9a）按gh轴展开，并与式（4-9b）联立得

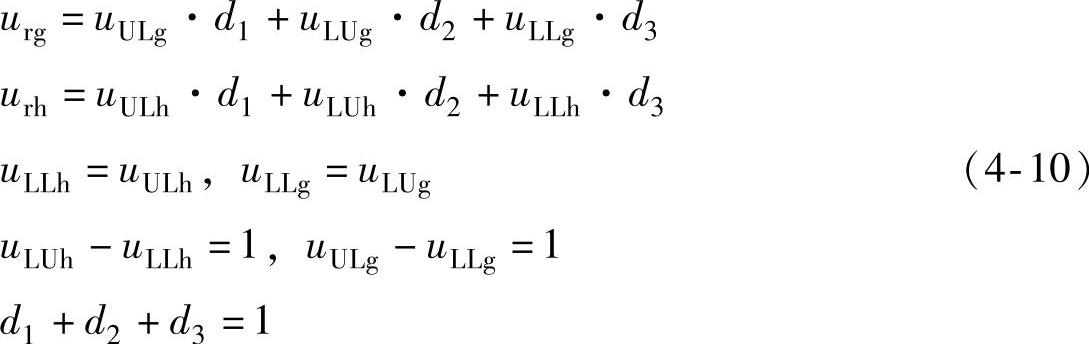
求解联立方程式（4-10），得

d₁=d_UL=u_rg-u_LLg

2）当u₃=u_UU时，类似可以得到：

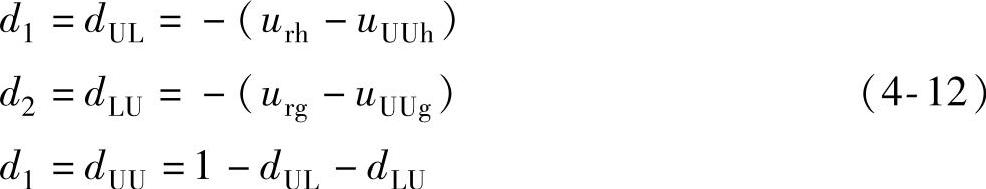
通过以上的推导，可以看出基于60°的坐标系能够简化大量的计算，弥补了传统算法的不足。