四象限运行控制的优化标题

1.逆变状态的产生

逆变状态可以通过下述步骤实现：

1）当电动机处于发电状态时，负载能量回馈到直流侧，造成直流母线电压升高，实际检测的直流母线电压信号U_d比给定的直流母线电压信号U_d^*大，经过控制算法运算和整流器的控制，使实际的直流母线电流减小，如此循环，直至减小为0，之后变成负值（直流母线电流反向），PWM整流器便进入逆变状态。

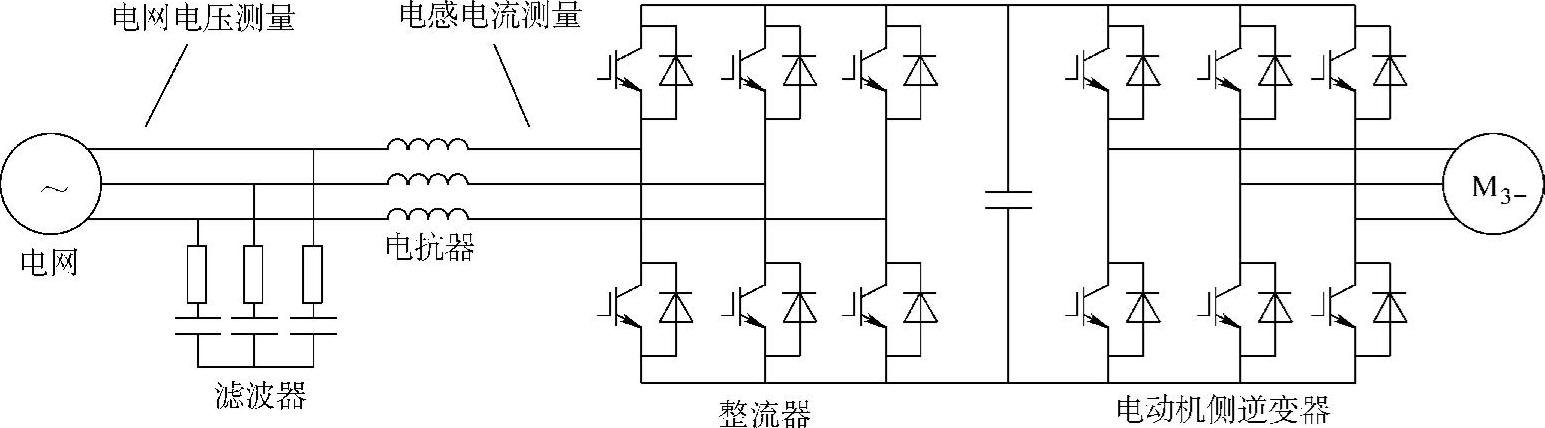
图3-28 双PWM变频器的主电路拓扑

2）根据图3-24，通过对u_s幅值和相位δ的控制，可以使i比u超前或滞后一角度φ，便可调节功率和功率因数，δ为u和u_s的夹角。当调节u_s超前电源电压u相位角δ，此时电路便处于逆变状态。当使u与电路电流i反相，如图3-29所示，则为功率因数为1的逆变状态，整流器向电网回馈有功功率能量。

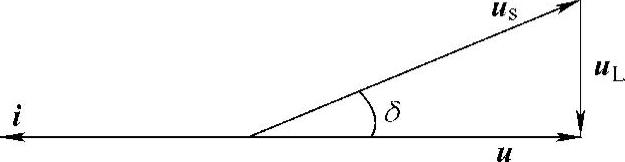
图3-29 逆变状态矢量图

2.四象限运行的控制

步骤如下：当变频调速系统工作于第一、三象限时，使u与电路电流i同相，电路工作于整流状态。当系统工作于第二、四象限时，可使u与电路电流i反相，电路便工作于逆变状态，完成四象限运行。

当双PWM变频器系统采用SVPWM技术控制时，可采用两片DSP芯片分别控制整流器和逆变器，其算法可参考上面所述的单独控制算法，但两片DSP芯片需有同步措施，不再重述。

[注1]矢量控制动态方程

以定子电流i_s、转子磁链Ψ_r和转速ω为状态变量，用MT表示按转子磁链定向的坐标系，并使M轴与转子磁链矢量同向，即令Ψ_r=Ψ_rd、Ψ_rq=0、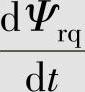=0，可得异步电动机转子磁链定向的状态方程：

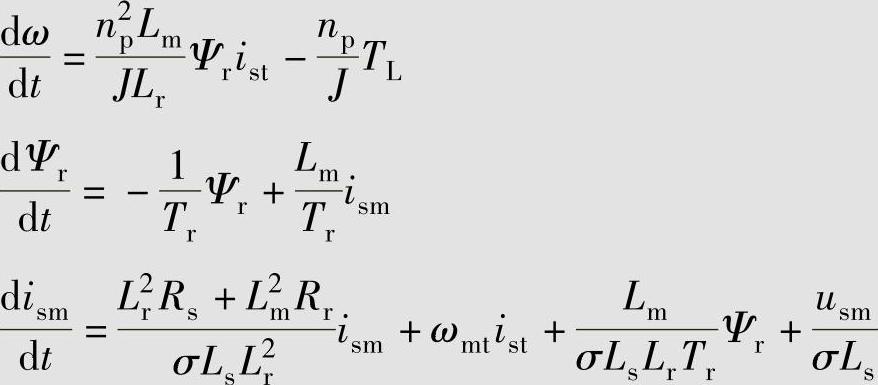
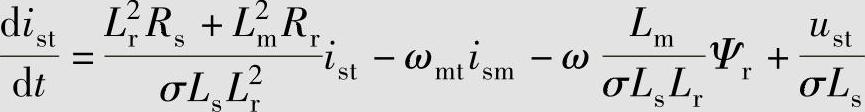
式中 σ——电动机漏磁系数，。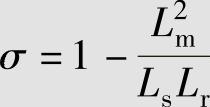

电磁转矩为

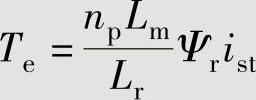(www.xing528.com)

转子磁链的旋转角速度：

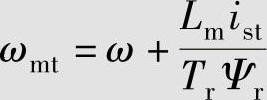
按转子磁链定向的数学模型将定子电流分解为励磁分量i_sm和转矩分量i_st，电磁转矩正比于转子磁链与定子电流转矩分量的乘积，转子磁链的幅值与旋转角速度均受定子电流的控制，与定子电压无直接的关系。因此，就转子磁链和电磁转矩而言，按转子磁链定向的动态模型属于电流控制型。

[注2]直接转矩控制动态方程

以定子电流i_s、定子磁链Ψ_s和转速ω为状态变量，采用按定子磁链定向（仍用dq轴变量表示），使d轴与定子磁链矢量重合，则Ψ_s=Ψ_sd、Ψ_sq=0、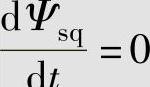，异步电动机按定子磁链定向的动态模型为

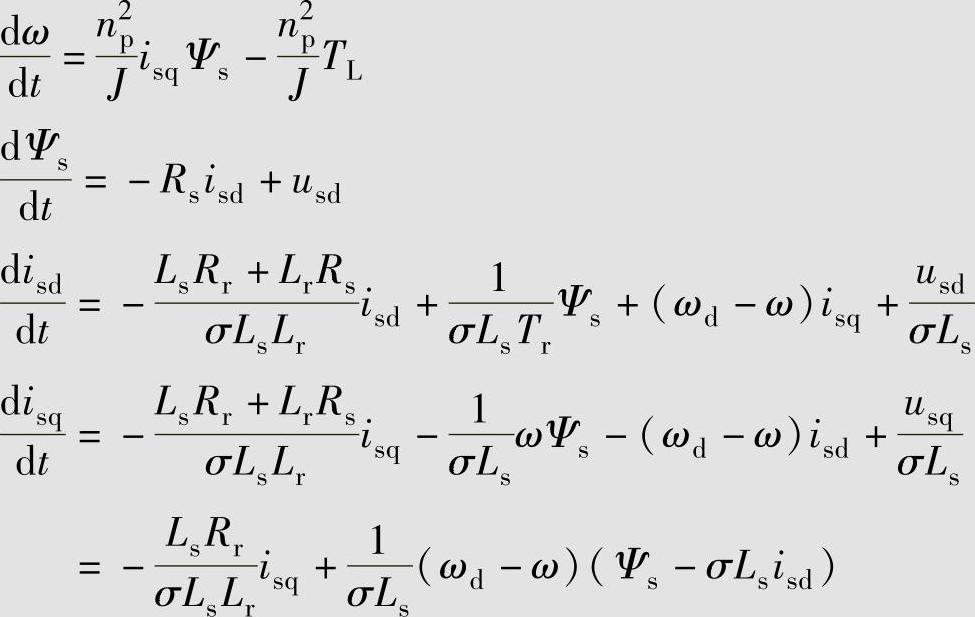
电磁转矩：

T_e=n_pΨ_si_sq

由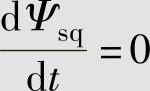可得，定子磁链旋转角速度：

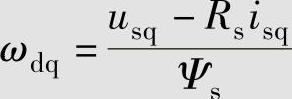
按定子磁链定向，也可将定子电流分解为转矩分量i_sq和励磁分量i_sd，电磁转矩与按转子磁链定向的转矩表达式在结构上相同，但定子磁链的幅值与旋转角速度分别受定子电压的控制，是受电流扰动的电压控制型。

Ψ_s=L_si_sd-σL_s（ω_dq-ω）T_ri_sq

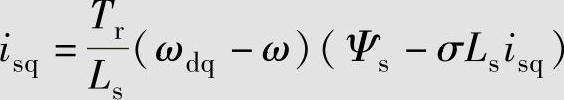
由此可得：

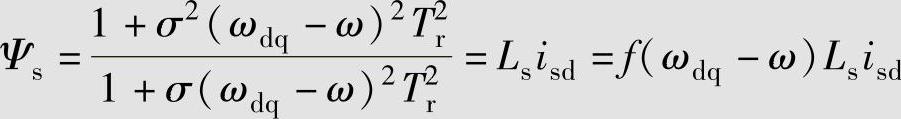
在理想空载时，ω_dq=ω，则Ψ_s=L_si_sd。随着负载的增加，（ω_dq=ω）2增大，由于σ较小，故f（ω_dq-ω）＜1，导致定子磁链减小。因此，定子电流的转矩分量呈去磁作用，其耦合程度大于按转子磁链定向。