SVPWM功率滞环控制系统的优化方法

1.系统的构成与工作原理

根据上述，通过适当地控制，可以解决功率低下的问题，能使功率因数为1；还可以使变频器的输入电流波形为正弦波，抑制谐波分量和保持直流电压恒定。具体的方法不少，这里采用有功和无功直接控制的方法，将ABC三相坐标系转换为dq坐标系，根据dq坐标系下的数学模型，结合滞环控制和矢量控制优点，构成功率滞环SVPWM整流器控制系统如图3-25所示。该系统的特点是以保持功率因数等于1为目标，采用双闭环，外环采用电压PI调节器（AVR）控制的电压环，保证输出电压稳态无误差；内环采用滞环控制的电流环，使电流响应更加快速，使整流器具有良好的动态特性和鲁棒性；而SVPWM控制提高了直流利用率。

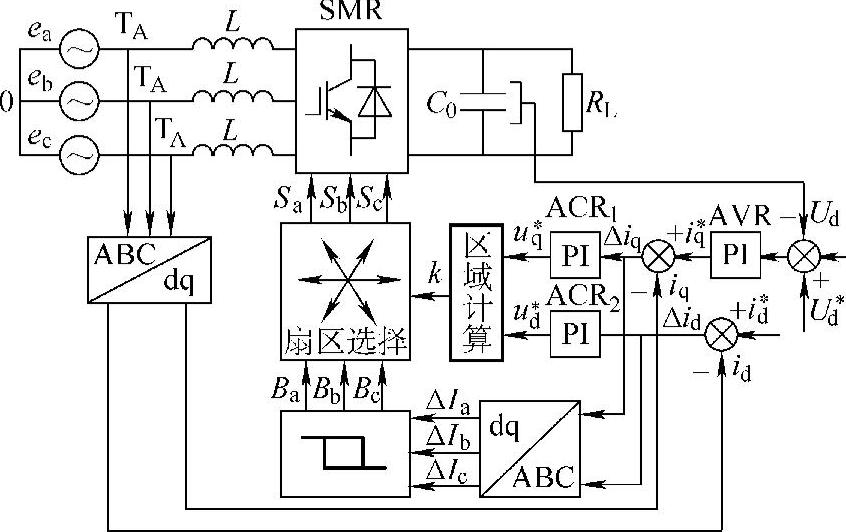
图3-25 功率因数为1的SVPWM功率滞环控制系统

AVR输出为内环电流控制提供电流有功分量i_q的参考值i_q^*，为获得功率因数为1，则电流的无功分量i_d的参考值i_d^*=0。交流侧的电流信号通过ABC/dq变换获得实测值i_d、i_q分别与i_d^*、i_q^*比较，其误差值Δi_dΔi_q通过积分环节分别得到交流侧指令电压矢量u^*在d、q轴上的投影值u_d^*，u_q^*；进而可判断u^*所在区域及其相应的状态信号值B_a.B_b.B_c。

2.控制算法

下面讲述系统算法。设αβ坐标系为两相静止坐标系，当t=0时，d轴与α轴重合，dq坐标系以角速度ω逆时针旋转。图3-26所示为u^*的dq坐标分解，由此可得u^*与α轴夹角θ为

u^*所在的第K扇区与θ的关系为

式中 INT——取整数。

具体控制过程如下：

图3-25中区域计算框所用公式为式（3-27）及式（3-28），得到u^*所在区域k，k=i，以Ru^*（i）表示，i=1，2，…，6。(www.xing528.com)

图中dq/ABC坐标变换框得到ΔI_a、ΔI_b、ΔI_c3个误差值，经过滞环调节器比较，得到对应的三相状态信号B_aB_bB_c。B_aB_bB_c有j种组合，j=1，2，…，6。每种组合用R_ΔI（j）表示，它们的对应关系如式（3-29）所示。B_a表示ΔI_a>0，B_a表示ΔI_a＜0，B_b、B_c仿此。电流滞环控制原理与图3-9和图3-12相同。

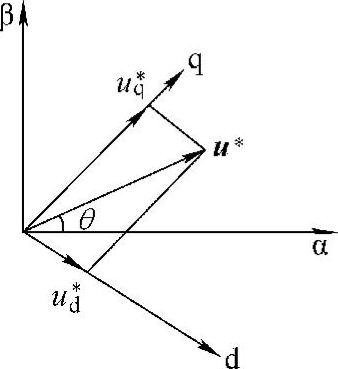
图3-26 u^*的dq坐标分解

表3-10为R_ΔI（j）、Ru^*（i）与输出电压矢量u_k的选择。已知所在区i和所要的开关信号j，从表中查出所要的电压矢量u_k，便得到输出三相开关状态S_a、S_b、S_c，以此进行控制整流器，达到功率因数为1的目的。

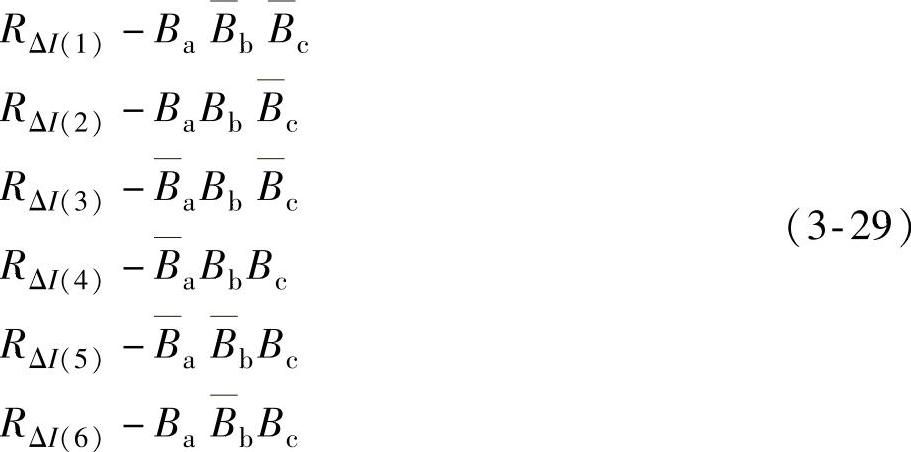
表3-10 R_ΔI（j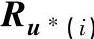）、与u_k的选择

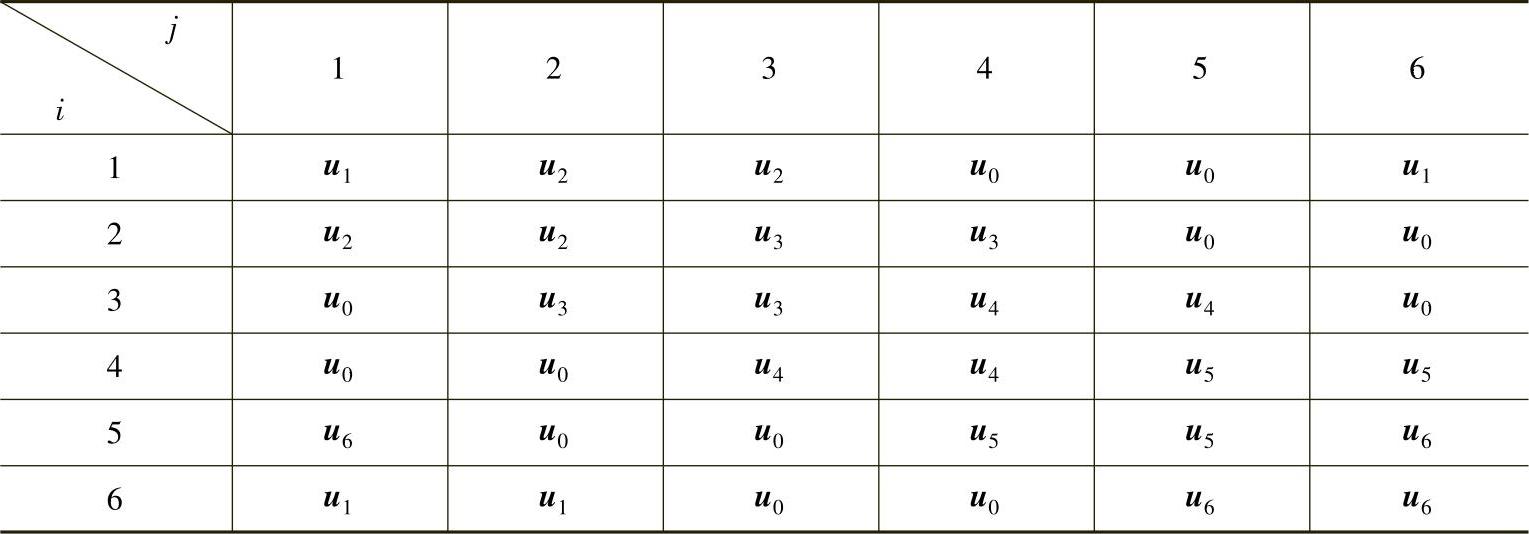
图3-27所示为a相电压、电流的仿真及负载实验结果波形。

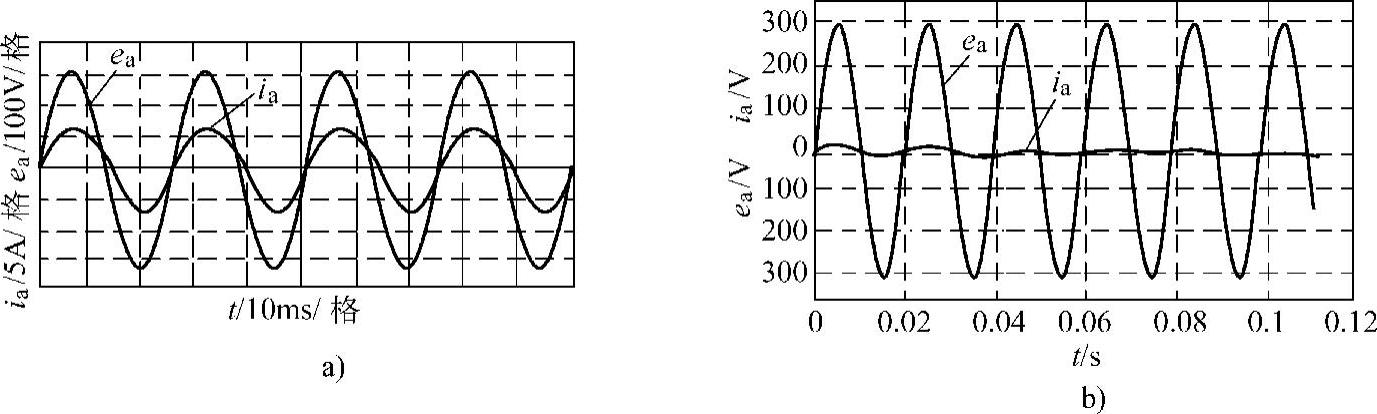
图3-27 a相电压电流波形

a）仿真 b）实验结果