电压矢量与Ψ、Te的关系探究

为了选取合适的电压矢量，必须了解电压矢量与Ψ、T_e的关系；在此基础上方能确定哪个电压矢量符合系统的控制要求。讨论这个问题常联系到两个公式：

1.转矩公式

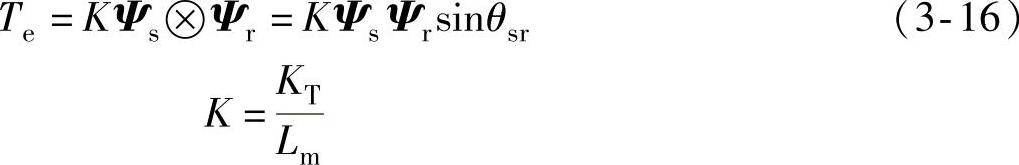
式中 K_T——电动机结构时间常数；

L_m——互感系数；

θ_sr——定转子磁链间的夹角，如图3-10所示；

——叉乘。

电动机正常运行过程中，θ_sr的值变化范围不大，其平均值也较小，故式（3-16）还可以简化为

T_e=KΨ_sΨ_rθ_sr （3-17）

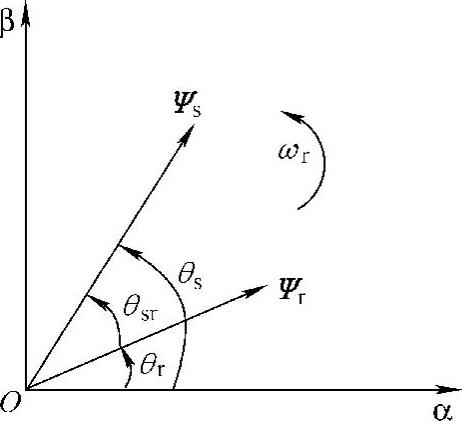
图3-10 转子和定子磁链图

直接转矩控制只对电动机磁链进行控制，由于其控制的时间很快，每一个采样周期要进行一次运算和控制，所以其等效的时间常数很小，在此周期可以认为，转子磁链的大小和方向均未发生变化。同时也可认为定子磁链幅值大小不变，则式（3-17）中电动机的转矩只与θ_sr有关，故控制θ_sr的大小，即可控制输出转矩。

式（3-16）只说明电动机转矩与磁链的关系，分析应如何控制转矩，还未涉及电压矢量的关系。

2.动态方程式

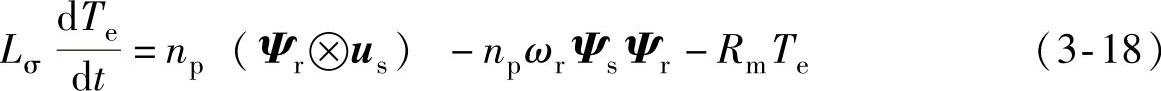
式中 R_m=R_sL_r/L_m+R_rL_s/L_m(www.xing528.com)

L_σ=（L_sL_r-L_m）2/L_m

L_s、L_r分别为定子和转子的电感

式（3-18）联系到电压矢量u_s和Ψ_s、Ψ_r及T_e的关系，说明当施加超前于定子磁链Ψ_s的电压矢量u_s，使dT_e/dt＞0时，转矩会增加。当施加落后于定子磁链的电压矢量或零矢量，使dT_e/dt＜0时，转矩会减少。

式（3-18）只是定性地表述，仍然未能符合直接转矩控制的实用要求，我们要求的是：根据定子磁链与电磁转矩偏差的符号以及当前定子磁链矢量所在的位置，选取合适的空间矢量，实现对定子磁链与电磁转矩的控制。

根据上述要求，下面介绍一个简单的方法，用到一个基本公式：

Ψ_s=u_st （3-19）

这个方式是当定子磁链定向直接转矩控制时，将空间电压矢量沿定子磁链相同的方向和垂直方向分解，得到（u_sd、u_sq）分量。以图3-11所示的扇区Ⅰ为例，两个分量见表3-1。忽略定子电阻压降，当u_sd为正时定子磁链幅值加大；当u_sd=0时，定子磁链维持不变；当u_sd为负时，定子磁链幅值减小。同理，当u_sq为正时，定子磁链矢量正向旋转，电磁转矩加大，当u_sq=0时，定子磁链矢量停在原处，ω=0，电磁转矩减小；当u_sq为负时，定子磁链矢量反向旋转，产生制动转矩。这个规律可以推广到其他扇区。

图3-11 电压矢量与Ψ、T的关系

表3-1 （u_sd、u_sq）分量正负极性

另一篇文献对磁链和转矩的变化趋势也有论述，对扇区Ⅰ，施加电压矢量与链、转矩变化趋势情况见表3-2，此结论与上述基本一致。

以上分析了一个扇区内定子磁链与电磁转矩的变化规律，可以推广到其他几个扇区。因此，我们可以根据定子磁链与电磁转矩和给定值的偏差，以及当前定子磁链矢量所在的位置，选取合适的空间矢量，实现对定子磁链与电磁转矩的控制。

表3-2Ψ_s、T_e变化趋势