一般闭环变频调速系统虽然有较好的控制效果,但与直流调速相比,差距仍较大。大家知道,直流电动机调速之所以得到高性能的转矩转速控制,是由于电枢电流和磁场磁通可以分开独立控制,异步电动机却不能做到。异步电动机的转矩可写成:
T=KTΦI2cosφ2 (3-1)
式中 I2——转子电流有效值;
cosφ2——转子电路功率因数;
Φ——旋转磁场每极的主磁通;
KT——与电动机结构有关的常数。
由于这些电磁量为交流电磁量,笼型转子电流I2又不能测量,故要想和直流机一样直接对Φ、I2独立分开控制是困难的。但是本节所讲述的矢量变换控制技术,能够将交流量变成直流量,只要测出定子侧电压、电流,就能对磁通和电流进行独立控制。此种控制技术的基本思路是按照产生同样的旋转磁场的等效原则建立起来的。
我们知道,三相交流异步电动机通入三相交流电,便形成角速度为ω的旋转磁场,对应于定子交流的频率fs。三相绕组分别相差120°,互相耦合,如图3-1a所示的ABC坐标系。另外,我们还知道,多相交流电动机通以平衡电流,同样也可以产生旋转磁场,如两相交流电动机通以电流iα、iβ,也能产生旋转磁场,两相励磁绕组互相垂直,不相耦合,如图3-1b所示的αβ坐标系。如果ABC坐标系和αβ坐标系的旋转磁场磁势和角速度相同,则可认为二者是等效的。再看一台直流电动机,当输入直流可分为励磁电流iM和电枢电流iT时,也能产生旋转磁场,两个绕组也互不耦合,互相垂直,如图3-1c所示的MT坐标系。如果它的旋转磁场和上面所述两种相同,则它们都是等效的。所谓等效,就是它们的物理量,如电流、电压等,可以等效变换。
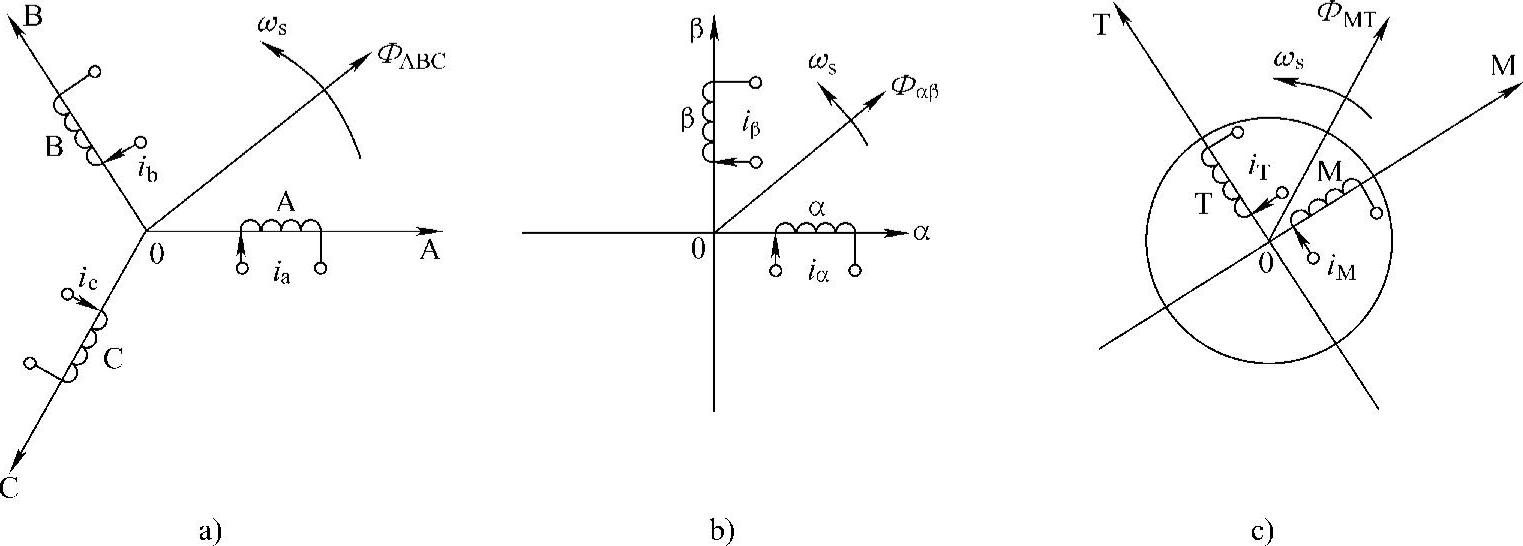
图3-1 异步电动机等效模型
a)三相坐标系 b)两相坐标系 c)MT坐标系
按照变换原则,ABC坐标系和αβ坐标系的变换与反变换(叫做Clark变换),αβ坐标系和MT坐标系的变换与反变换(叫做Park变换)分别为

A1、A2为变换矩阵,A1-1、A2-1为逆矩阵。在矢量变换控制过程,必须经过坐标变换,即要从三相ABC坐标系变换为两相αβ坐标系(3/2变换),再从αβ坐标系变换到直流MT坐标系,并且还要反过来变换(两相反变换为三相称为2/3变换),因此需要求出变换矩阵A1、A2和A1-1、A2-1。现述从ABC坐标系变换为αβ坐标系。
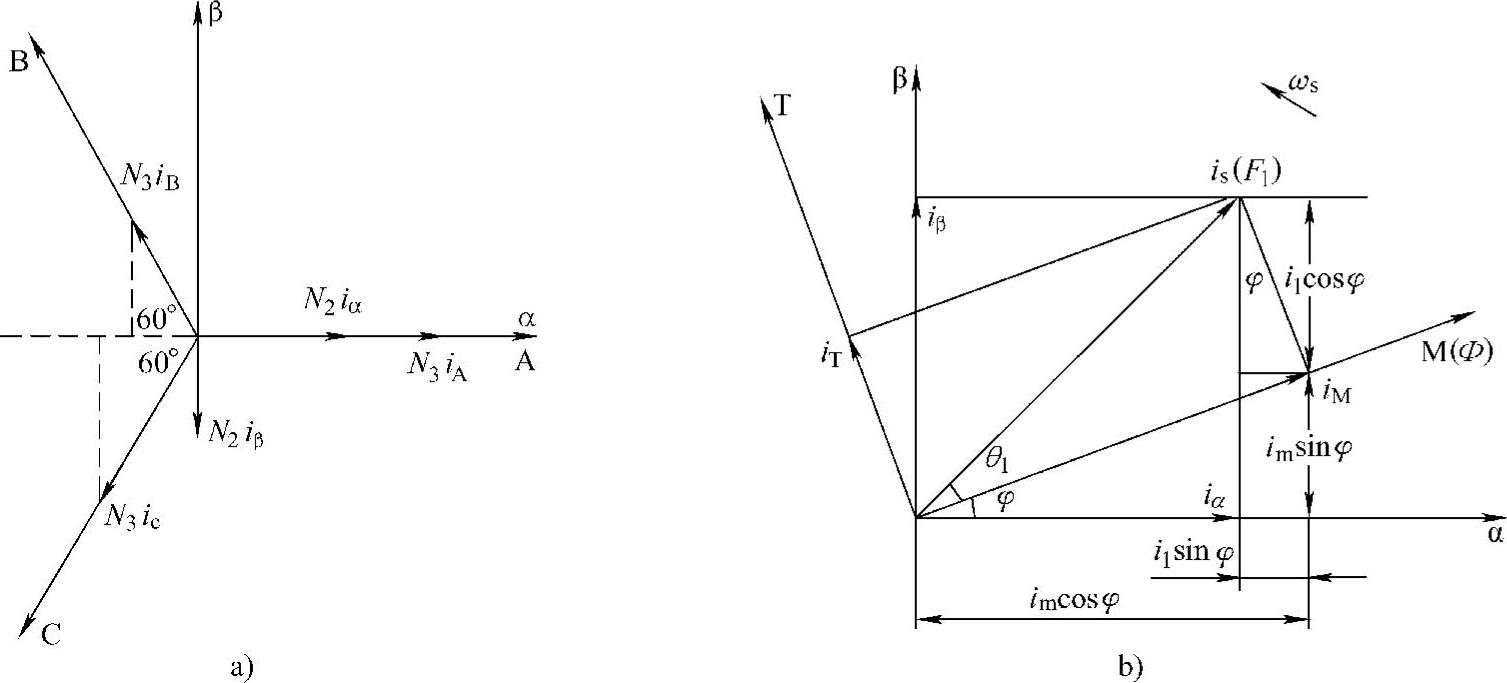
图3-2a所示为ABC坐标系和两相交流绕组αβ坐标系矢量的变换关系,令αβ坐标系的α轴与ABC坐标系A相重合,当两个坐标系等效,将ABC坐标系变换为αβ坐标系时,有
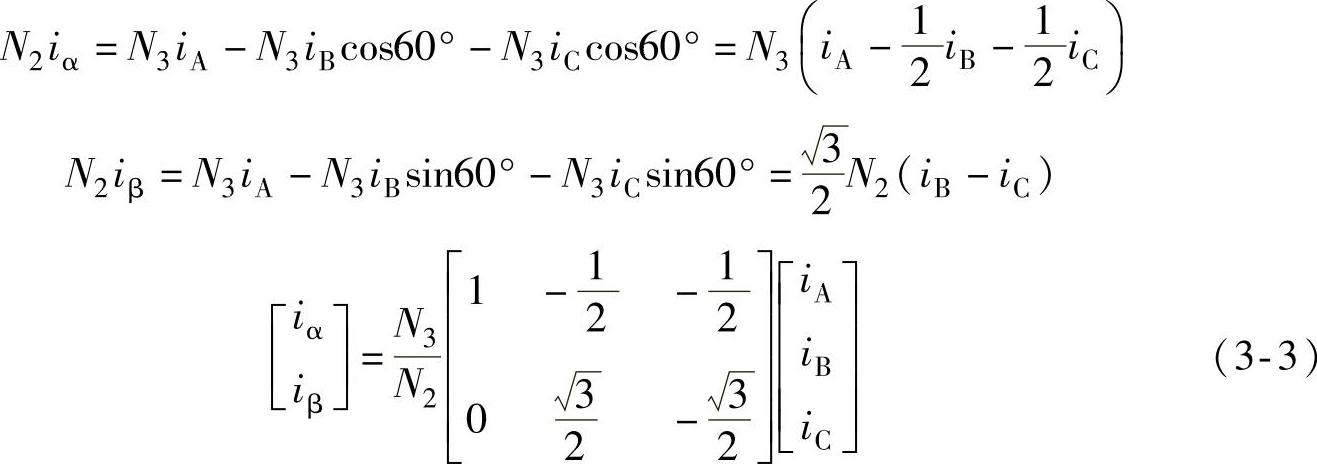
变换矩阵:
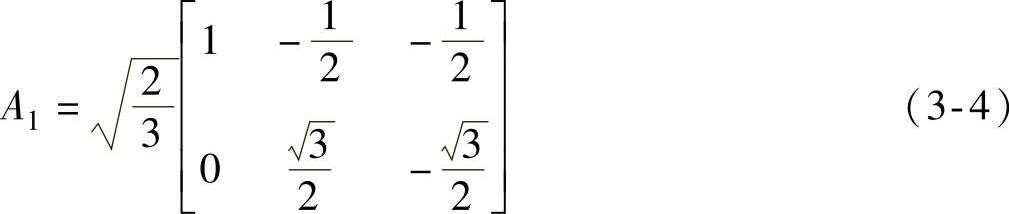
逆矩阵: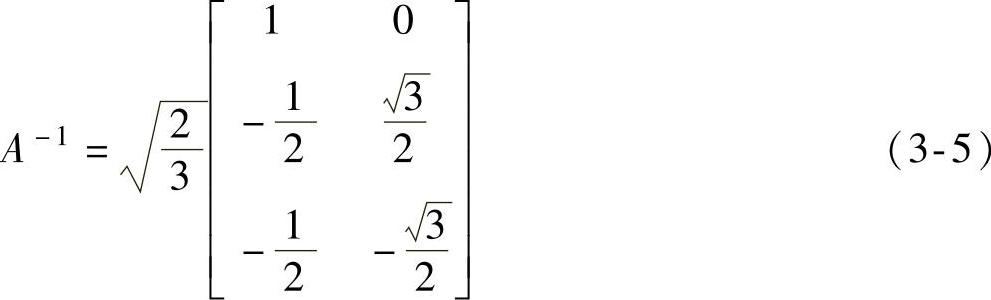
 (https://www.xing528.com)
(https://www.xing528.com)
图3-2 坐标变换
a)ABC坐标到αβ坐标变换 b)αβ坐标到MT坐标变换
图3-2b所示为αβ坐标系和直流MT坐标系的矢量关系,MT坐标系和αβ系坐标的交角为φ,它以ωs旋转,故称旋转坐标系,而前两种则称为静止坐标系。转子磁链方向沿M轴方向相重合,叫做转子磁场定向。这时电动机各电磁量以定子流is为例,矢量关系如图3-3所示。可以看出,is对于αβ坐标系来说是交流量,is在MT坐标系的分量iM、iT是直流量。我们还可以看出,iM是产生磁通的,iT与磁通的乘积就是电动机的转距;如果通过变换从is得到iM和iT,二者解耦,我们可以对磁通和转子电流分开独立控制,达到和直流电动机那样控制转矩转速的目的。
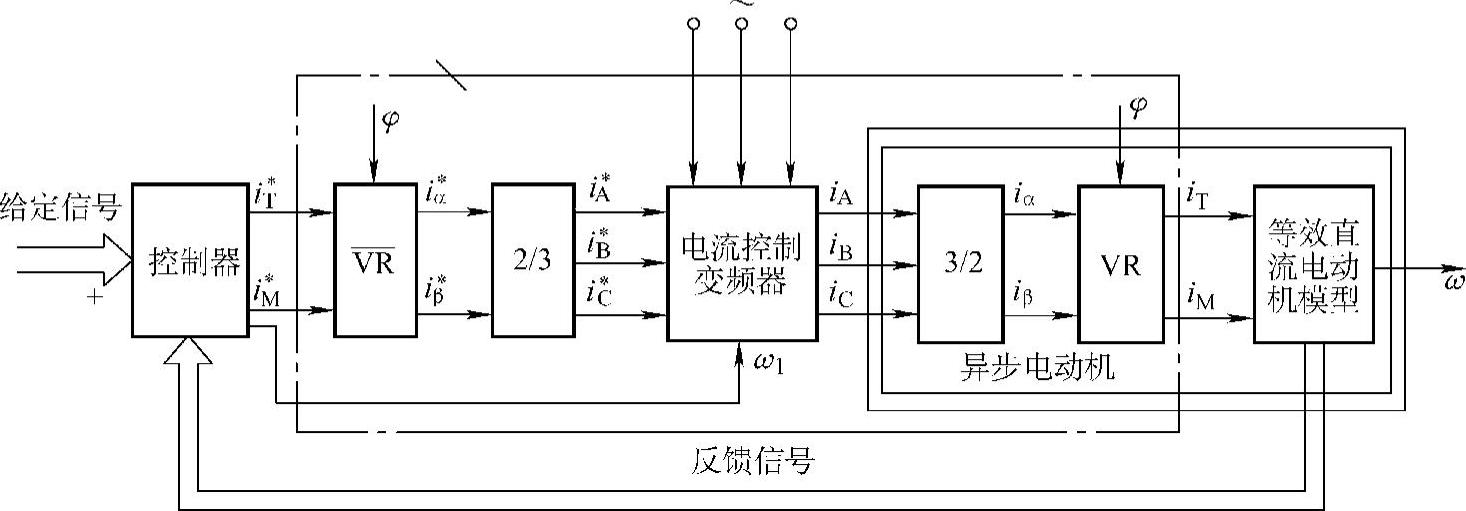
图3-3 矢量变换控制系统框图
现在来按Park变换原则求两坐标系的矢量变换矩阵A2,从图3-3可得
iα=iMcosφ-iTsinφ
iβ=iMsinφ+iTcosφ
写成矩阵形式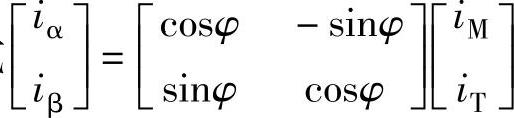
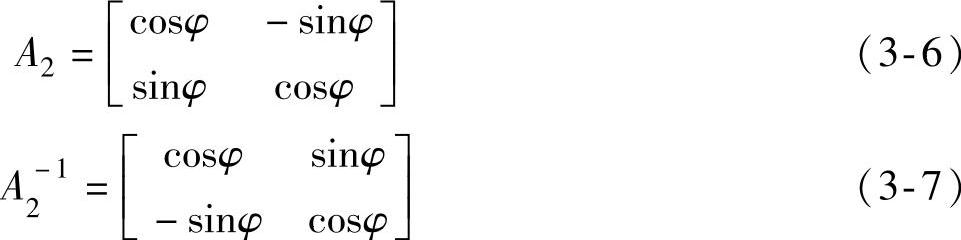
由于三种旋转磁场等效,所以,MT直流绕组与ABC交流绕组等效,即有
iMT=A2iαβ=A2A1iABC (3-8)
由止式可知,MT直流绕组中的电流iM、iT与三相电流iA、iB、iC之间必存在着确定关系,因此通过控制iM、iT就可以实现对iA、iB、iC的瞬时控制,达到控制转矩转速的目的。
矢量控制为何要进行坐标变换?大家知道,三相异步电动机的数字模型是一个高阶、非线性、强耦合、多变量的系统,只有通过这种变换才能简化换算,主要是可以解耦和降阶。通过两次变换,可得到励磁电流iM、转矩电流iT和电磁转矩Te的公式[注1]:
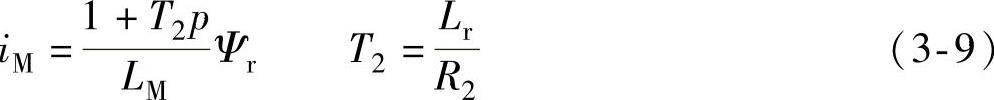

从上列公式可知,Te只与iT有关,iT和iM解耦,当Ψr为常数时,转矩正比于iT,故控制iT即可控制转矩,和直流电动机相似,效果可与之媲美。
根据上述,矢量变换控制过程可用图3-3所示的系统框图来描述:三相交流输入变频器,变频器输出三相VVVF交流去驱动异步电动机(右侧);用传感器测出电流,经3/2变换,得到iα、iβ(不计零序分量),再经旋转变换VR,变成直流量iT、iM。信号传到控制器(左侧)控制后得到给定直流量iT*、iM*,先经旋转反变换 ,得到给定交流量iα*、iβ*,再经2/3变换得到三相给定控制信号iA*、iB*、iC*,控制变频器输出电动机运行电流。应注意的是此处变频器为电流控制型,若为电压控制变频器,应当用变换器将iα*、iβ*变为uα*、uβ*。
,得到给定交流量iα*、iβ*,再经2/3变换得到三相给定控制信号iA*、iB*、iC*,控制变频器输出电动机运行电流。应注意的是此处变频器为电流控制型,若为电压控制变频器,应当用变换器将iα*、iβ*变为uα*、uβ*。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




