如上所述,欲使磁链轨迹为圆,开关器件不能按u1、u2…顺序切换,而要采用别的切换方式。上面已介绍了一类可行的方法,得到的磁链轨迹为不等边多角形,控制较复杂,开关器件切换较多,使损耗增大。目前常用的是引入零矢量的电压矢量合成法,得到的磁链轨迹是正多边形,控制有规律性,较为简便。这种方式是将圆周等分为若干小段,用两个相邻的电压矢量交替切换,使其合成矢量等效这段弧的弦,来近似这一小段弧。这样不断切换下去,形成一个逼近圆形的正多边形,这种方法叫做矢量合成法。
矢量合成法引入了零矢量。所谓零矢量,是指逆变器开关器件VT1VT3VT5或VT2VT4VT6同时导通,逆变器输出电压为零,此矢量记为u0、u7。或u0(00 0)、u7(111),而上述的u1~u6称为非零矢量。零矢量输出虽为零,但在SVPWM中可起重要的作用。
如图2-11所示,将磁链轨迹圆周等分为若干小段(6的倍数),取一小段ab,可用它的弦来近似。弦ab不一定和基本电压矢量方向一致,可用两个相邻的矢量合成。矢量选择方法可按下述:将 矢量移到电压空间矢量分布图中,点与零点重合,
矢量移到电压空间矢量分布图中,点与零点重合,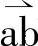 方向和原来的方向相同,可见
方向和原来的方向相同,可见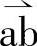 落入扇区Ⅵ(见图2-4),可由u6、u1两个矢量合成,由此可获得参与合成矢量为u6、u1,如图所示。其原因是这两个矢量与
落入扇区Ⅵ(见图2-4),可由u6、u1两个矢量合成,由此可获得参与合成矢量为u6、u1,如图所示。其原因是这两个矢量与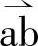 相近,其他矢量是无法满足合成要求的。
相近,其他矢量是无法满足合成要求的。

图2-11 等分段矢量合成法
得到参与合成矢量为u6、u1后,将电压矢量u6和u1交替切换(参看图2-11右角放大图),即在a点选择电压矢量u6向c点移动,经历一定时间到达c后,再选择电压矢量u1向b点移动,经历一定时间到达b点,那么磁链矢量轨迹就从a移到b,按上述方法以一定的线速不断改变切换电压矢量,一段一段地接下去,磁链轨迹就是一个逼近于圆的正多边形。由于每段相等,控制起来比较简单,抑制谐波的效果也较好。现在来介绍各个电压矢量所需持续时间或工作时间(例如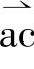 、
、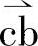 等所经历的时间也就是相关开关器件导通时间)的确定方法。
等所经历的时间也就是相关开关器件导通时间)的确定方法。
将图2-11右上方小图重绘,如图2-12所示,这种切换共由2段组成,电压矢量切换顺序为u6-u1。因矢量移动线速恒定,|up|=Ud,按式(2-2),矢量持续时间(器件导通时间)与相应的轨迹长度成正比,即
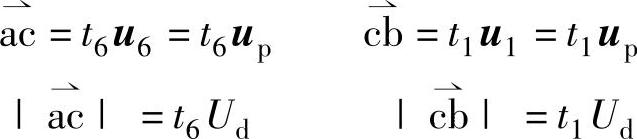
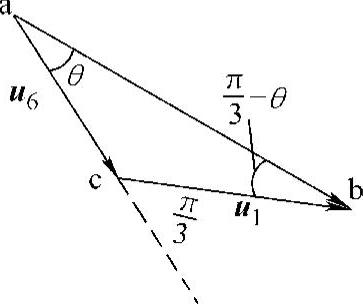
图2-12 合成矢量的求法
式中 t6、t1——分别为u6、u1持续时间,也称工作时间。
因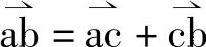 ,设
,设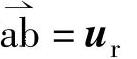
故有
urT0=t6u6+t1u1
式中 T0——开关周期。
实际上看,从a到b的时间不一定为t6+t1,这样就有移动的角速度不等于给定角速度(给定频率)的问题。为使磁通矢量移动角速度为给定的ω,常引入零矢量来调节磁通矢量从a到b移动的总时间。上文说过,所谓零矢量,是指逆变器(见图2-1)中开关器件VT1、VT3、VT5或VT2、VT4、VT6同时导通,逆变器输出电压为零,此矢量记为u0或u7。零矢量一般放在程序开始或结束时,可防电压跳变。但为了少用零矢量,在矢量合成切换时,若前个矢量是u1、u3、u5,宜插入u7;反之为u2、u4、u6时,则插入u0。
若u6和u1引起的总工作时间造成角速度大于或小于ω时,可加入零矢量u0或u7持续时间来调节,将平均角速度准确调节为ω。设引入零矢量后切换顺序变为u7—u6—u1,u7经历时间为t7,则ab一段的总时间为
T0=t7+t6+t1
式中 T0——ab一段经历的时间,称为开关周期。
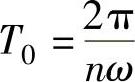
式中 n——小段数;
ω——给定角频率。
设u6、u1合成输出电压矢量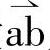 为ur,则合成磁链矢量轨迹为
为ur,则合成磁链矢量轨迹为

应用正弦定律,由图2-12有
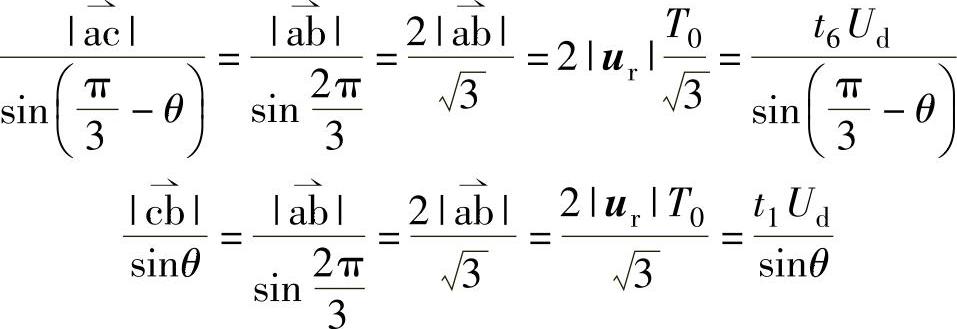
便可得: (https://www.xing528.com)
(https://www.xing528.com)
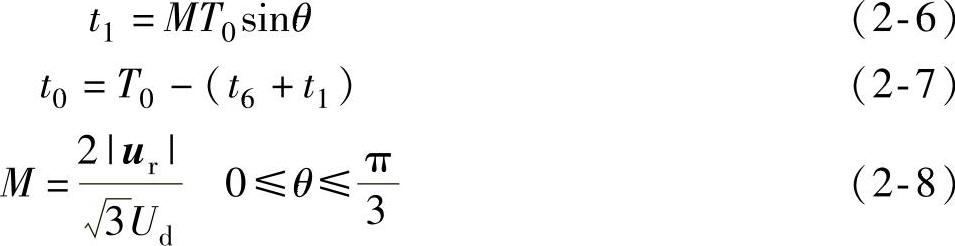
式中 θ——起始矢量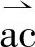 与合成矢量
与合成矢量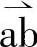 的夹角;
的夹角;
M——调制深度或直流电压的利用率。
应用式(2-5)~式(2-8)时,ur按U/f=常数取U值,T0=2π/nω,ω为给定角速度,n为所分小段数。
若取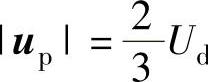
则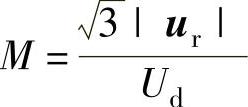
观察式(2-7),当t0=0,T0*=t6+t1,T0*<T0,此时为没有零矢量的周期,小于原来的周期,那么电动机就要加速;在此基础上,若加入零矢量,情况就相反,转速就要降低。同理,如延长零矢量的时间,可以延长周期的时间,即降低了转速;反之减少零矢量时间,就可以减少周期时间,即使电动机增速,所以零矢量有调节转速作用。
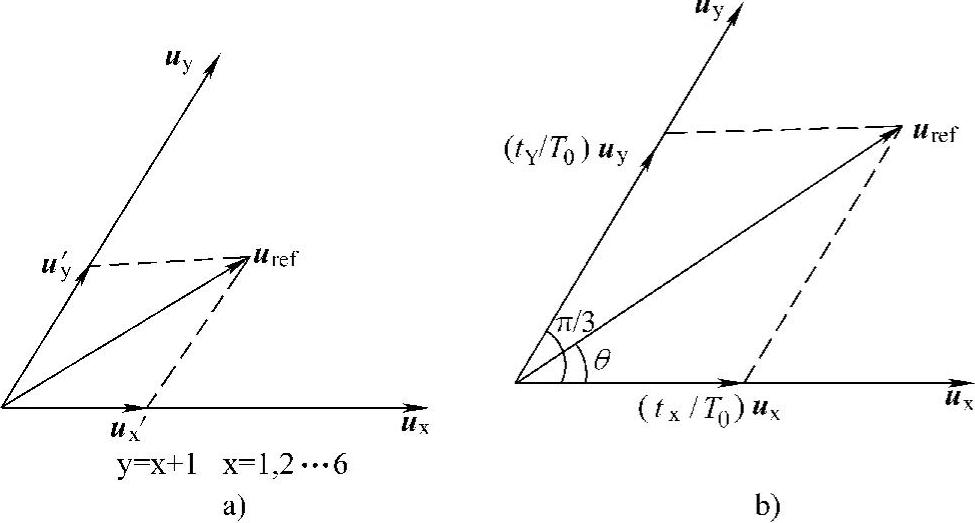
图2-13 矢量合成图
图2-12所示磁链圆弦上的矢量合成与图2-4中基本电压空间矢量分布中扇区Ⅵ的矢量合成等效,也就是矢量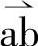 处于扇区Ⅵ中。实际上圆周上任一段矢量都可以落入对应的扇区;若把
处于扇区Ⅵ中。实际上圆周上任一段矢量都可以落入对应的扇区;若把 称为逆变器所要的输出电压矢量uout,则任意一个电压矢量uout可落入图2-4中所示对应的一个扇区。如图2-13a所示,任意一个电压矢量uout可用两个相邻基本电压矢量ux(起始矢量)、uy(终止矢量)合成;uout相当于图2-12中矢量
称为逆变器所要的输出电压矢量uout,则任意一个电压矢量uout可落入图2-4中所示对应的一个扇区。如图2-13a所示,任意一个电压矢量uout可用两个相邻基本电压矢量ux(起始矢量)、uy(终止矢量)合成;uout相当于图2-12中矢量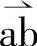 或文中的ur,常作为期望的逆变器控制矢量,又称目标参考矢量,简称参考矢量uref,也有些文献用us或u*表示。导通时间计算和上述相同。通常也用占空比来表示合成,如图2-13b所示,参与合成的基本矢量归化到磁链,应当分别为乘以持续时间tx、ty,这里用占空比(tx/T0)ux、(ty/T0)uy表示,(tx/T0)ux、(ty/T0)uy相当于图2-12中的
或文中的ur,常作为期望的逆变器控制矢量,又称目标参考矢量,简称参考矢量uref,也有些文献用us或u*表示。导通时间计算和上述相同。通常也用占空比来表示合成,如图2-13b所示,参与合成的基本矢量归化到磁链,应当分别为乘以持续时间tx、ty,这里用占空比(tx/T0)ux、(ty/T0)uy表示,(tx/T0)ux、(ty/T0)uy相当于图2-12中的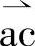 、
、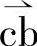 。θ为起始矢量与合成矢量的夹角。按照正弦定律可得
。θ为起始矢量与合成矢量的夹角。按照正弦定律可得
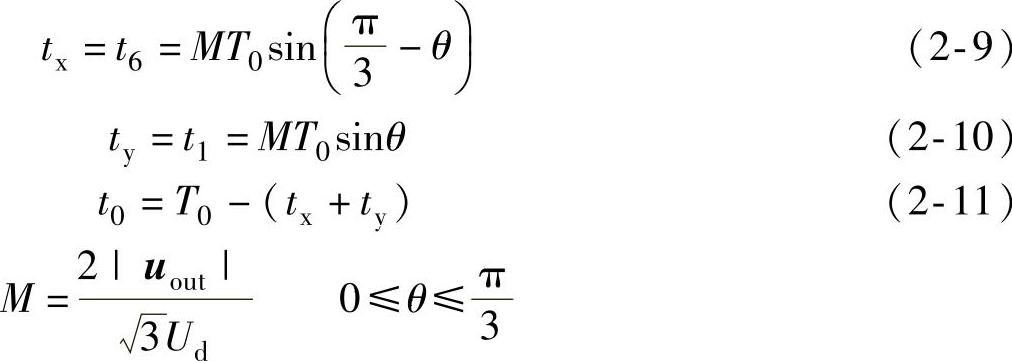
可见与前面推导完全相同。
值得注意的是,当运行中电动机突然加、减速时,控制系统提供的电压矢量值uout可能超过逆变器输出的最大电压矢量值,叫做过调制。为了保证合适的电压矢量脉宽调制方案,电压矢量持续时间要加以修正。方法之一是用限制开关导通时间的办法,首先计算出当前两个参与合成的矢量作用时间tx、ty,并判断tx+ty>T0是否成立,若成立,则计算修正值。设修正后两个相邻非零矢量时间为t′x、t′y
因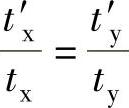
故

t0=0(零矢量时间)
式中 T0——开关周期。
式(2-9)~式(2-11)式适用于图2-11以后连续各小段电压矢量经历时间的计算,只要按要求选择起始矢量和终止矢量(均为相邻矢量),便可合成磁链矢量。按此顺序使有关开关器件进行切换,磁链轨迹图形便是逼近圆形的正多边形。这种调制方式便于使用计算机控制,调制效果也较好。
毫无疑义,此种合成模式,段数越多就越接近圆形,效果就越好。但当段数很多时算法甚为复杂,难于计算和控制,开关损耗也很大,所以一般只取少数小段(6的倍数)构成正多边形来近似,应用例子如图2-14所示。这个例子用上述连续切换的磁链矢量轨迹Ψt1-Ψt12来近似,每小段相隔30°,共12段,每一段对应一个θ0角(以β轴为起点),选择对应的电压矢量(两个相邻非零矢量和一个零矢量)及计算持续时间,合成矢量使磁链矢量连接起来,即可得到轨迹为12正多边形的磁链,接近于圆,谐波分量大为减小。各小段所要的电压矢量和持续时间如图2-15所示。应注意的是,电压矢量空间分布图是与图2-4不同的。
图2-15所示为一个调制周期(12T0)工作数据,在不同角度时ux、uy对应的值和它们的持续时间,应根据当时的uout或uref位置来选择,即此值选定对应的ux、uy及tx、ty、t0或t7,其位置由当时采样的θ角来确定。
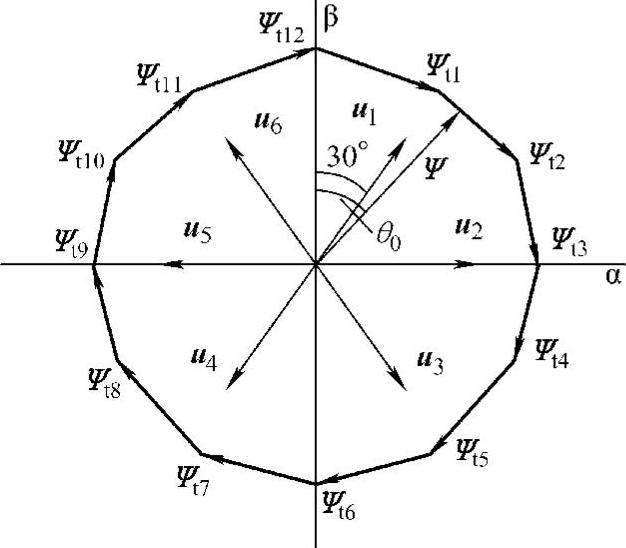
图2-14 12段构成的磁链轨迹图形
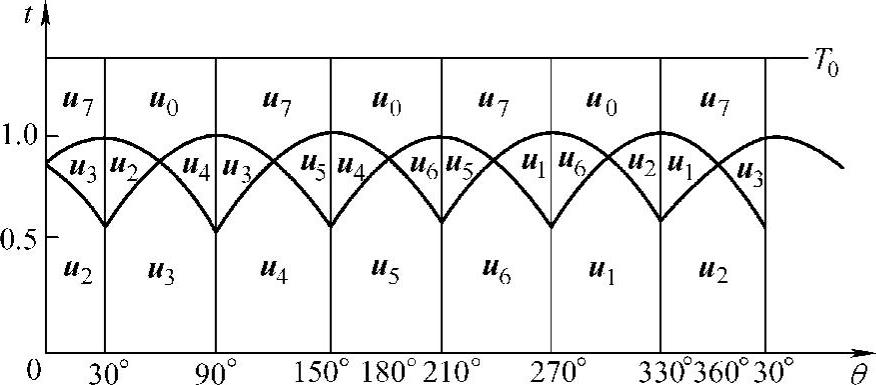
图2-15 电压矢量和持续时间
SVPWM控制需要许多数据和大量计算,用模拟电路实现是困难的,必须借助计算机,但总的来说,比SPWM简便。当采用微机控制系统运行时需要提供必需的数据。电压矢量脉宽调制所需的主要数据是电压矢量的持续时间t,当段数分得很细时,这将是一个相当大的数字。提供这些数据的方法有二:其一是离线计算后存入计算机存储器,供运行时调取,相当于查表法;其二是运行时在线实时计算,及时提供。从采样到算出输出符合给定的过程就是SVPWM控制算法。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




