解密密钥集合的乘积——群组规模为5的公钥立方体结构

以离散对数基础构造结构化公钥结构，设给定一个素数p，有限域乘法群上一个生成元g，进一步扩展DH（Diffie-Hellman）协议，公开加密密钥为｛gai（modp），0≤i≤n｝，合法解密密钥组成解密密钥集合｛xi｝，加密解密方式参见文献，公钥中的参数｛aij｝和解密密钥集合｛xi｝之间的关系如下：

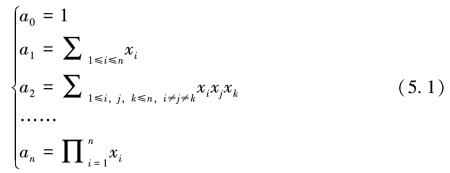
根据多项式公式系数定理，得到一元n次多项式由此，组成公开加密密钥参数｛aij｝为方程f（x）的系数，而解密密钥是方程f（x）的根。根据系数的标号将公钥分为从第零层到第n层，每层的公钥材料是解密密钥集合排列组合之和，由此，组织公钥材料，系数a1对应第一层公钥材料｛gxi（modp），1≤i≤n｝；系数a2对应第二层公钥材料为系数a3对应第三层，公钥材料为以此类推，针对系数an，形成公钥材料为立方体高度值等于秘密解密密钥规模，由此形成的公钥材料数量为

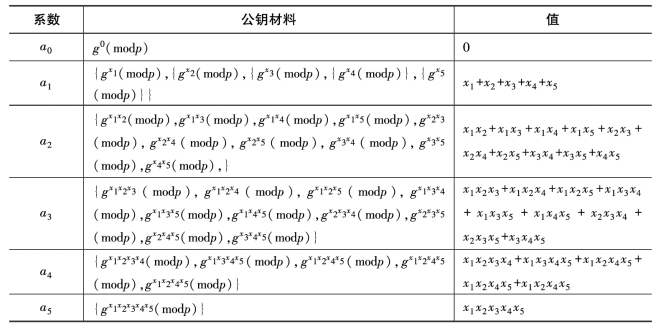
例如一个群组规模为5的网络中，共有31份公开加密密钥资料，每个成员ui具有一个解密密钥xi，则公钥材料为表5.1所示。

表5.1 群组规模为5的结构化公钥结构

群组规模为5的公钥立方体结构如图5.1所示。

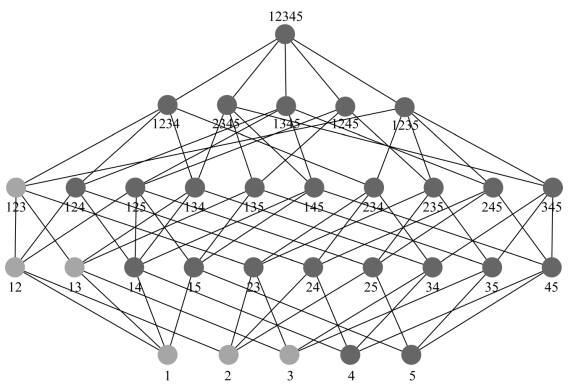
图5.1 群组规模为5的公钥立方体结构

定义5.1：公钥立方体结构是解密密钥集合的全排列组合的乘积集合。

定理5.1：已知n+1个解密密钥，可生成n+1层公钥立方体。(www.xing528.com)

证明：采用归纳法证明，解密密钥集合规模为1时，即｛x1｝，对应的公钥立方体为解密密钥集合｛x1，x2，…，xn｝规模为n时，可生成n层公钥立方体结论成立，立方体结构为（modp）｝｝。则规模为n+1的解密密钥集合，在n层公钥立方体的结构上，通过解密密钥xn+1计算n+1层公钥立方体，n+1层公钥立方体比n层公钥立方体增加部分为：

第一层计算并将该值加入n层公钥立方体的第一层密钥材料集合中。

第二层计算并将该值加入n层公钥立方体的第二层密钥材料集合中。

第三层计算n，｝，并将该值加入n层公钥立方体的第三层密钥材料集合中。

以此类推：

第n层计算并将该值加入n层公钥立方体的第n层密钥材料集合中。

第n+1层计算作为n+1层立方体的n+1层元素。

由此计算得到n+1层公钥立方体。

定理5.2：设存在n个解密密钥集合SKi，1≤i≤n，对应的公钥材料集合为和PKi，1≤i≤n，解密密钥集合和解密密钥任意两个集合满足关系SKi⊃SKj，1≤j＜i≤n，则对应的公钥立方体中密钥材料任意两个集合满足SKi⊃SKj，1≤j＜i≤n。

证明：由定理5.1得到。