平面度误差测量的示值数据处理方法

答：采用直接检测方法时，通过测量可直接获得测得平面各点坐标值；而采用间接检测方法时，所得示值则需进行数据处理，方可按误差评定方法求得其误差值。

当用水平仪、自准直仪法进行等跨距测量时，可直接用示值进行数据处理，最后将处理结果乘以系数K换算成线性值；也可先将示值乘以系数K换算成线性值后，再进行处理。

仪器分度值τ单位为毫米每米（mm/m）时，系数K=τ×L（K的单位为_μm）；仪器分度值τ′单位为角度值秒（″）时，系数K=0.048τ′×L（K的单位为μm）。式中L为桥板跨距（单位为mm）。

按照不同布点方式，分别将布点测量示值转换成坐标值。

（1）网格布点的测量示值转换成坐标值 方法是：以过起始点A的水平面作为转换基面，按测量顺序逐点累加，即可获得相对转换基面的坐标值Z_ij。如图284所示，测得一组测点的示值（图284a），按累加的办法得到各测点的坐标值（图284b）。

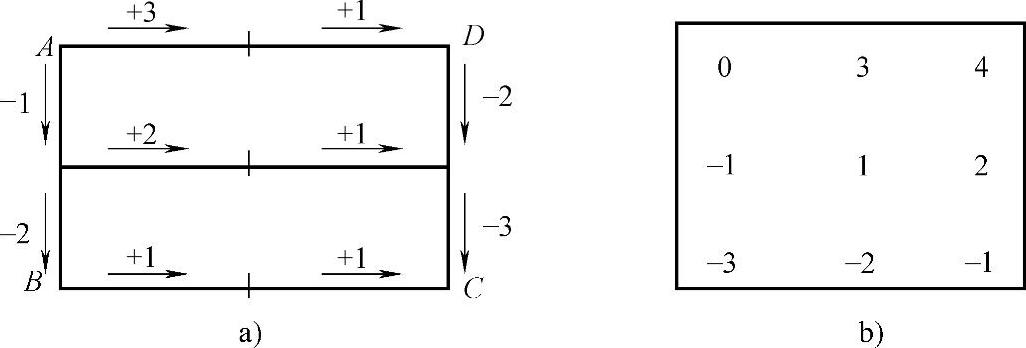
图284 网格布点的数据处理

网格布点整个测量过程是封闭的（图284a），从两个测量方向（A→D→C和A→B→C）累加所得C点坐标值Z_C理论上应相等。但因存在测量误差，两测量方向累加所得Z_C可能不同，其差值称为C点闭合差Δ。

当Δ（线性值）绝对值小于或等于不确定度允许值u₀时，可取两个Z_C的平均值为其坐标值，进行平差处理。平差处理后应将a′_ij重新转换成Z_ij。当Δ绝对值大于u₀时，一般应重新测量。

平差处理可按下式进行计算：

1）对A→D→C测量线：

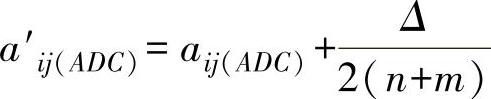
2）对A→B→C测量线：

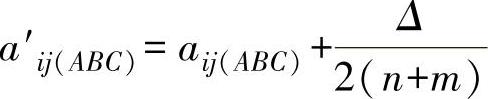
式中 a′_ij、a_ij——平差处理后与前各点示值。

n、m——纵、横方向布点数。

（2）对角线布点的测量示值转换成坐标值 如图279b所示，先将各测量线上测点的示值按测量顺序逐点累加的方法求得各点过渡坐标值Z′_i。通过平移和旋转，使AB测量线的B点末值与对角线BD的B点初始值相等；对角线BD的中点值与对角线AC的中点值相等，构成平行或通过A、B点和对角线交点H三点的一个平面，同时算出AB、AC、BD测量线上其余各点的坐标值。

通过平移和旋转，使AD、BC、DC测量线上的首末两点与转换后的AB、AC、BD测量线上的相应首末点等值，同时算出AD、BC、DC测量线上其余各点的坐标值。(www.xing528.com)

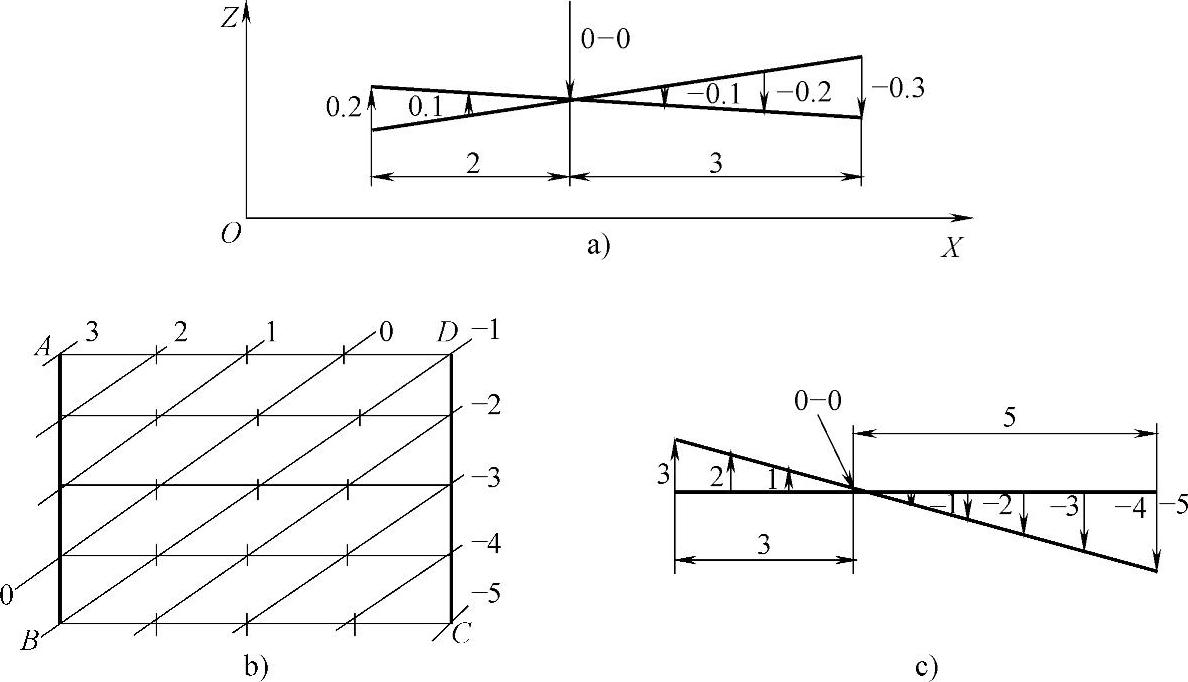
图285 坐标值旋转变化方法

通过平移和旋转，使P_iP′_i测量线上的首末点与转换后的AB、DC测量线上的相应点等值，同时算出P_iP′_i测量线上其余各点的坐标值。

上述坐标值旋转变化方法如图285所示，其变换步骤是：首先确定旋转轴0—0，按下式算出旋转系数K_a，即

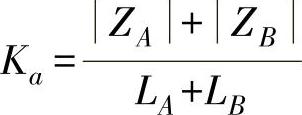
式中 Z_A——A点变换前后的坐标差之绝对值；

Z_B——B点变换前后的坐标差之绝对值；

L_A——A点距转轴0—0的距离；

L_B——B点距转轴0—0的距离。

按下式求出各测点的旋转量，升高者取正值，降低者取负值，即

Q_k=±K_aLk

式中 L_k——各旋转点至转轴的距离。

按下式求出各点旋转变换后的坐标值，即

Z_i′_j=Z_ij+Q_k

式中 Z_ij——各测点旋转变换前的坐标值。

面的旋转变换方法与上述基本相同，如图285b、c所示，以0—0为转轴面的旋转变换示例。