直线度误差评定的方法有哪些？

答：如上所述，通过各种检测方法，首先获得被测点坐标值，但并不能直接得到直线度误差值，而必须按照误差评定原则，根据误差评定精度需要（即满足生产要求）选用不同的评定方法，按作图法或计算法进行数据处理，方可求出相应的直线度误差值。

直线度误差评定方法有以下几种。

（1）最小包容区域法 以最小区域线作为评定基线的方法。此法最符合误差评定原则（最小条件），其评定结果小于下述最小二乘法和两端点连线法。

最小区域线是指构成直线度最小包容区域的两平行理想线之一或轴线。它根据测得要素按最小包容区域判别法来确定（见129题）。

最小包容区域的宽度或直径即为直线度误差值（具体评定方法见GB/T11336《直线度误差检测》6.1节）。

（2）最小二乘法 以最小二乘中线作为评定基线（或基线方向）求得直线度误差的评定方法。

最小二乘中线是指使实际直线上各点到该直线的距离平方和为最小的一条理想直线。它是根据测得点求得最小二乘中线，然后由实测点相对该线最大变动量求得直线度误差值（具体评定方法见GB/T11336《直线度误差检测》6.2节）。

（3）两端点连线法 以两端点连线作为评定基线（或基线方向）的直线度误差评定方法。

两端点连线是指实际直线上首末两点的连线。该评定方法简便，生产中应用最广泛。但由于其不符合最小条件判别原则，故在生产中出现争议时，仍应以最小包容区域法进行仲裁。

按两端点连线法评定直线误差的方法有：

1）作图法。将测点的坐标值，按一定比例绘制在坐标图上，并顺序连接各点得测得直线图形，按不同要求分别用下述方法求出直线度误差值。

①在给定平面上，如图260所示。首先在测得图形上绘出首末两点B、E的连线l_BE，然后沿Z方向量出各点在两端点连线l_BE上、下方最大、最小偏离量d_max和d_min。按下式计算得直线度误差值，即

图260 在给定平面上两端点连线法

f_BE=d_max-d_min

②在任意方向上，如图261所示。首先将各测点的坐标值（X_i、Y_i、Z_i）按一定比例分别绘制在XOZ坐标平面（图261a）和YOZ坐标平面（图261b）上，得到两个投影面内的测得直线图形，并分别连接两坐标图上首末两点B、E，得到两端点连线l_BE在两坐标平面上的投射线l_BE|XOZ和l_BE|YOZ。

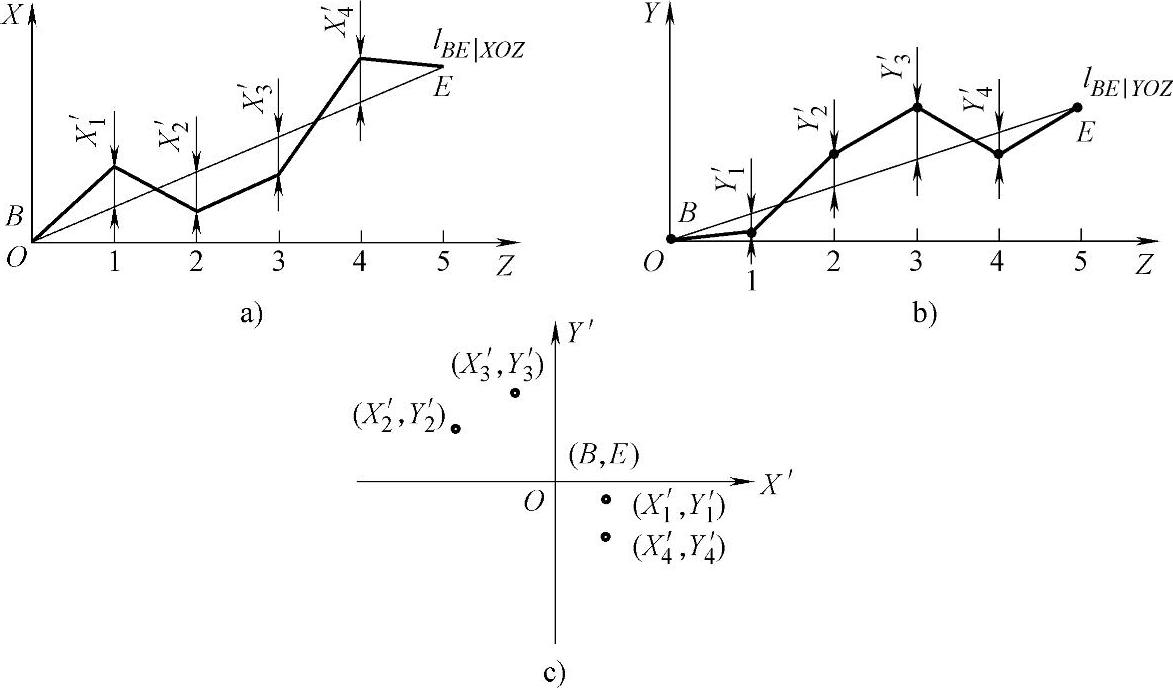
图261 在任意方向上两端点连线法

然后沿X、Y方向分别量取各测点到两端点连线l_BE的距离X_i′和Y_i′，且找出X′_i和Y′_i中的最大、最小值X′_max、X′_min、Y′_max、Y_m′_in。

将上述两投影面上最大、最小值点，投射到垂直于两端点连线l_BE的平面X′OY′上（图261c）。

按下述最大、最小值不同情况，采用不同作图方法，求出直线度误差值φf_BE。

a.两点情况。指两个坐标图中有一个坐标平面上的最大、最小值均为零，如图262所示。在XOZ坐标图上的最大、最小值为双向（图262a）或单向（图262b）分布，而在YOZ坐标图上最大/最小值均为零（图262c）。此时在单向或双向测得直线图形上，其纵坐标方向上的最大与最小值之差，即为其直线度误差值φf_BE（图262d、e）。

b.三点情况。在两个坐标平面上的最大、最小值均为单向分布，如图263所示。在XOZ坐标平面（图263a）和YOZ坐标平面（图263b）上的投影线均在两端点连线BE一个方向上。此时可按两坐标面内最大、最小值点在X′OY′投影面上的投影点来判别其误差值：当以距离最远两点的连线为直径作圆，如另一点位于该圆内时，则该圆直径即为其直线度误差值φf_BE（图263c）；如另一点不在圆内时，则应过三点作圆，其直径即为其直线度误差值φf_BE（图263d）。

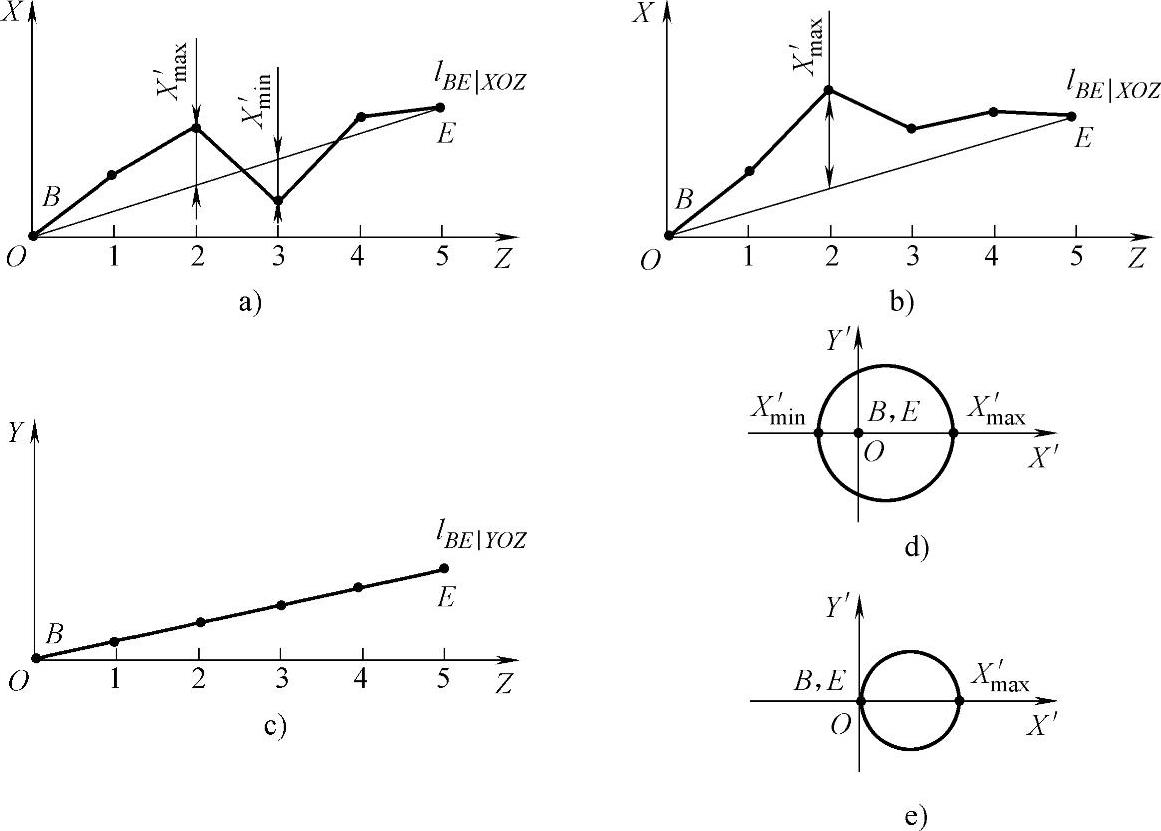
图262 两点情况

c.四点情况。一个坐标平面上最大、最小值为单向，而另外坐标平面上为双向分布，如图264所示。XOZ坐标平面上为单向（图264a）；YOZ坐标平面上为双向（图264b）。先在X′OY′坐标图上连接三个最大、最小值对应点和坐标原点构成四边形OA₃A₁A₂（图264c）。作四边形对角线，并以两对角线中较长者为直径作圆。若另外两对角点位于该圆内，则该圆的直径φf_BE即为直线度误差值；若另外两对角点中有一个位于圆外，则应以对角线两点与圆外点三点作圆，该圆直径为其直线度误差φf_BE。

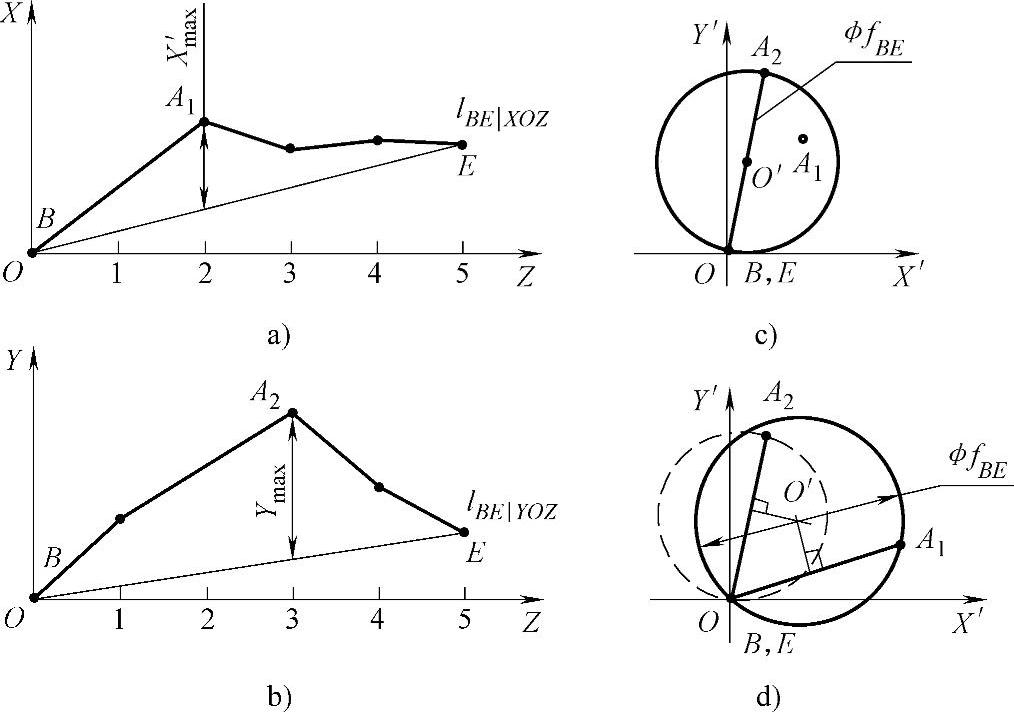
图263 三点情况

(www.xing528.com)

图264 四点情况

d.五点情况。两个坐标平面上的最大、最小值均为双向，如图265所示。XOZ坐标平面（图265a）和YOZ坐标平面（图265b）均为双向分布。评定其误差值时首先在X′OY′坐标图上连接四个最大、最小值点（图265c），形成一个四边形，若坐标原点在该四边形之内，则按上述四点作图方法求出直线度误差值φf_BE。

若坐标原点不在该四边形之内（图265d），则应连接五个点形成一个五边形，参照四点或三点作图法步骤，求出直线度误差值φf_BE。

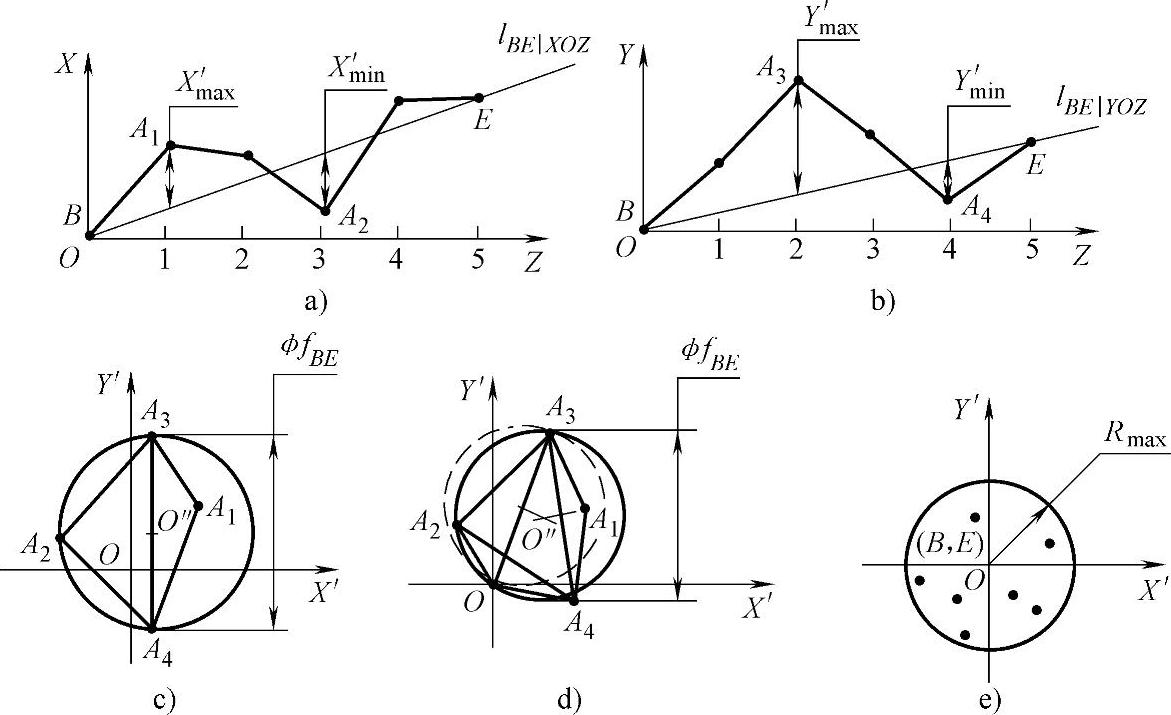
图265 五点情况

若各测点较均匀地落在X′OY′平面上多个象限内（图265e），则可求出各点距两端点连线的半径距离R_i，即

取其中最大值R_max的两倍，作为直线度误差φf_BE的近似值。

2）计算法。通过坐标转换求得直线度误差值。

①在给定平面（或给定方向、任意方向的投影）上。评定方法是：将两端点连线的始点定在原点上，列出各测点的坐标值，然后将测点坐标值Z_i，按下式转换为新的坐标值d_i，即

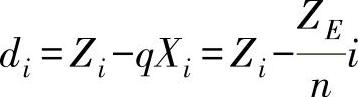
式中 Z_E——末端点坐标值；

q——方程系数，；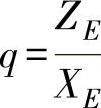

n——分段数。

根据各测点转换后新坐标值d_i，找出最大与最小值，两者之差即为该直线度误差值，即

f_BE=d_max-d_min

用两端点连线计算法求直线度误差过程示例见表36。

表36 用两端点连线计算法求直线度误差过程示例（单位：μm）

②在任意方向上。首先将起始点B定在原点上，如图266所示。然后根据各测点的坐标值，求出两端点连线l_BE的方程系数q、p，即

式中 X_E、Y_E、Z_E——末端点E的坐标值。

将各测点的坐标值代入下式，求出各测点距两端点连线l_BE的半径距离R_i，即

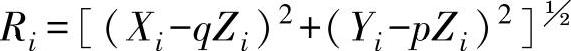
找出R_i中的最大值f₁，取其两倍（2f₁），即为该直线度误差值φf_BE。

图266 任意方向上计算法求直线度误差