案例设计步骤详解

1.数据的整理与描述

（1）编制各指标的综合数据表。

1）计算主要统计指标。使用Matlab、Excel软件，分别对三个地区以及综合统计表中的数据计算下面的统计指标：

样本总量：n

2）分析描述统计指标。比较平均数、中位数、众数的大小；偏度系数的大小、方向等。

（2）主要统计指标的分布。主要指标的符号说明：水资源价格P 1、资源出让价格P 2、政策处理费用X、水头Y、规模大小Z、水资源边际效益H、单位电能的投资I。

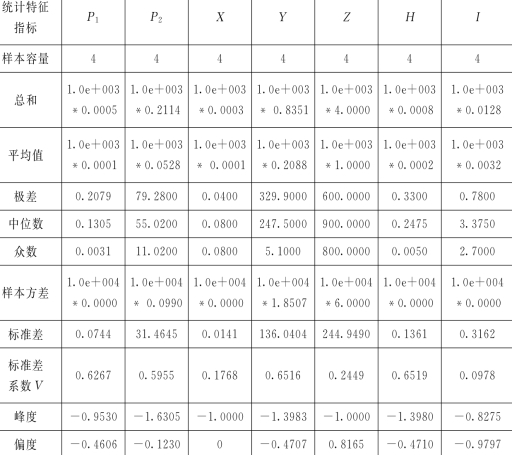
1）仙居县水权市场的主要统计指标见表1。从表1中可以看出，在仙居县水权市场中，指标P 1、P 2、X、Y、Z、H、I的最大 值 与 最 小 值 的 差 距 分 别 为0.2079，79.2800，0.0400，329.9000，600.0000，0.3300，0.7800。指标P 1、P 2、Y、H呈现轻度偏态，指标Z、I呈现一定偏态，指标X不呈现偏态，关于平均值对称。观察各指标的平均值与方差，了解各指标的平均水平及其偏离平均水平的程度。

表1　仙居县水权市场的主要统计指标

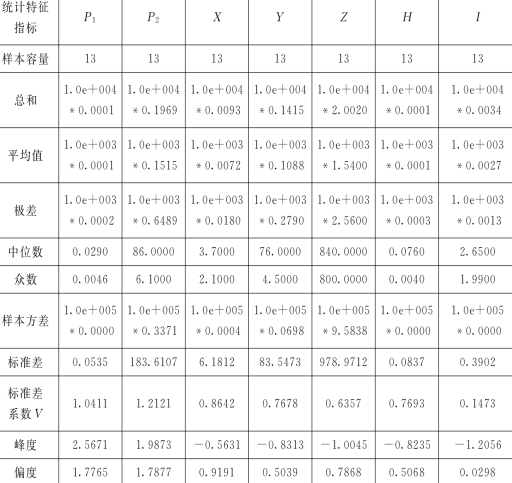
2）江山市水权市场的主要统计指标见表2。从表2中可以看出，在江山市水权市场中，指标P 1、P 2、X、Y、Z、H、I的最大值与最小值的差距分别为1.0e+003*0.0002，1.0e+003*0.6489，1.0e+003*0.0180，1.0e+003*0.2790，1.0e+003

*1.5400，1.0e+003*0.0003，1.0e+003*0.0013.指标P 1、P 2呈现较高偏态，指标X、Y、Z、H呈现一定偏态，指标I几乎不呈现偏态。

表2　江山市水权市场的主要统计指标

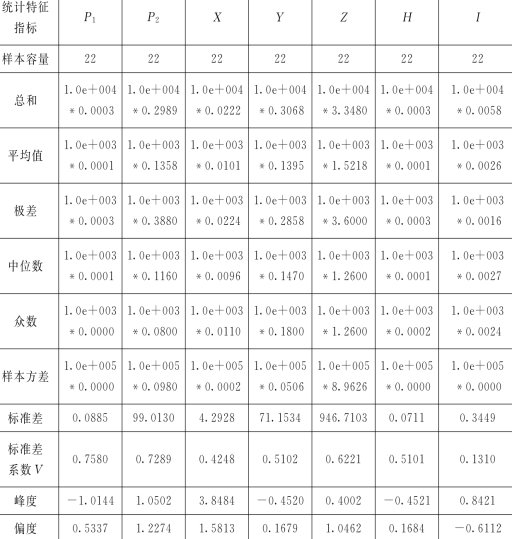
3）遂昌县水权市场的主要统计指标见表3。从表3中可以看出，在遂昌县水权市场中，指标P 1、P 2、X、Y、Z、H、I的最大值与最小值的差距分别为1.0e+003*0.0003，1.0e+003*0.3880，1.0e+003*0.0224，1.0e+003*0.2858，1.0e+003*3.6000，1.0e+003*0.0003，1.0e+003*0.0016.指标P 2、X、Z呈现较高偏态，指标P 1、I呈现轻度偏态，指标Y、H呈现轻度偏态。

表3　遂昌县水权市场的主要统计指标

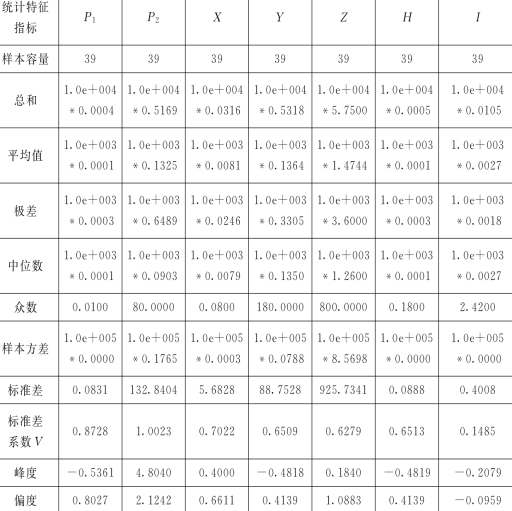
4）三个市场的综合统计指标见表4。从表3中可以看出，在水权市场中，指标P 1、P 2、X、Y、Z、H、I的最大值与最小值的差距分别为1.0e+003*0.0003，1.0e+003*0.6489，1.0e+003*0.0246，1.0e+003*0.3305，1.0e+003*3.6000，1.0e+003*0.0003，1.0e+003*0.0018.指标P 2呈现高偏态，指标P 1、X、Z呈现一定偏态，指标Y、H呈现轻度偏态，指标I几乎不呈现偏态。

表4　三个市场的综合统计指标

2.相关分析与线性回归分析

（1）水资源价格模型。该部分相关分析与线性回归分析的主要内容是研究6个主要指标P 1、X、Y、Z、H、I间的相互关系问题。这些指标之间有无关系？若有关系，关系的紧密度如何？存在的是什么样的关系？通过以下分析，可以知道影响各地区水资源价格的主要因素，以及变量间的变化趋势。

由于水权市场中数据量不足够多，从而对这些主要指标的认识不够深入，不能判断这些指标是否服从联合正态分布。在此情形下，使用惯用的正态相关分析显得有些缺乏理论支持。于是，下面使用等级相关分析，分别计算三个地区水权市场以及综合水权市场中6个指标间的相关系数。

斯皮尔曼等级相关系数公式

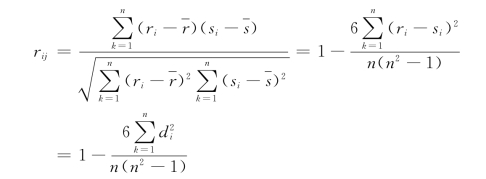
其中r P1（i）、r X（i）、rY（i）、r Z（i）、r H（i）、r I（i）分别表示在第i个水电站中P 1、X、Y、Z、H、I样本数据的等级。

1）仙居县水权市场。

a.水权价格相关指标间的关系研究见表5。

表5　仙居县水权市场中6个指标的等级数据

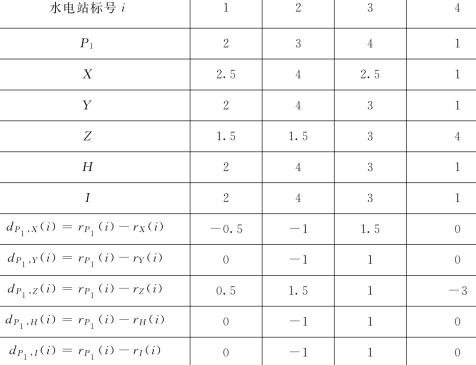
计算皮尔曼等级相关系数见表6。

表6　仙居县水权市场中的皮尔曼等级相关系数

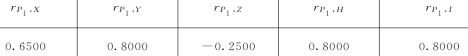
显著水平α=0.10，样本容量n=4，则r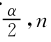=r0.05，4=0.8000。

结论：根据表6，在仙居县水权市场中，水资源价格P 1与水头Y、水资源边际收益H、单位电能投资I表现出较强相关性，与政策处理费用X表现出一定的相关性，与规模效应Z表现出微弱相关性，其中与水头Y、水资源边际收益H、单位电能投资I相关性的程度相当；与水头Y、水资源边际收益H、单位电能投资I、政策处理费用X表现出正相关，与规模效应Z表现出负相关。

b.线性回归分析。线性回归分析是用线性函数关系近似描述相关关系的表现形式，反映各变量间的变化趋势或规律，分为多元线性回归和一元线性回归。

多元线性回归分析：

根据上述分析，P 1与X、Y、Z、H、I间都表现出一定的相关性，所以建立下面的五元线性回归函数：

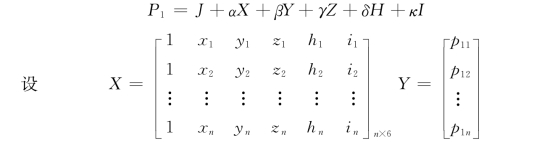
计算下面统计量：

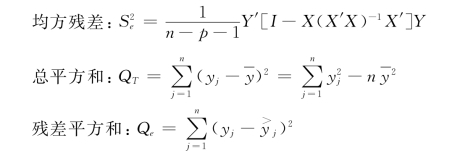
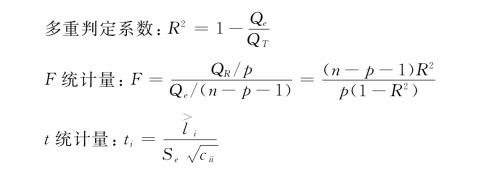
使用Excel及Matlab软件计算以上统计量，得到表7。

表7　线性回归统计量

各回归系数的t统计量为：

t=1.0e-006×[0+0.4796i，0.1673，0+0.2269i，-0.1439，0+0.1251i]

五元线性回归方程为：

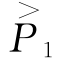=1.7500-7.7500X+0.0039Y-0.0004Z-4.0000H-0.3125I

以上数据中出现复数，这是不允许的。在检验回归系数显著性的t检验中，自由度γ=n-p-1，而此处γ=4-5-1=-2＜0，这是不可能的。所以，这里不适合使用多元线性回归。下面给出一元线性回归。

一元线性回归分析：

从相关性的分析不难知道，水资源价格P 1与水资源的边际效益H的相关系数较高，实际上水资源的边际效益直接影响了水资源的价格，建立如下的一元线性回归函数：

P 1=J+δH

使用Excel及Matlab软件计算相关的统计量，得到表8。各回归系数的t统计量为：

表8　线性回归统计量

t=2.7283

一元线性回归方程为：

回归系数说明，每增加一个单位水资源边际效益，水资源价格增加0.4857单位。从判定系数分析，水资源边际效益对水资源价格的影响中，有78.82%可以被该一元线性回归方程解释。

回归分析中，要求随机项均值为0，并服从正态分布。从统计量F分 析，查表得F 0.05（1，2）=18.51，因 为F=7.4438＜18.51，所以回归效果在水平α=0.05下不显著，即P 1与Z没有显著的线性关系。从统计量t分析，γ=4-1-1=2，α=0.05，查表得t0.05，2=4.303，所以回归系数在水平α=0.05下不显著。因此，线性回归方程不合适。

2）江山市水权市场。

a.水权价格相关指标间的关系研究见表9。

表9　江山市水权市场中6个指标的等级数据

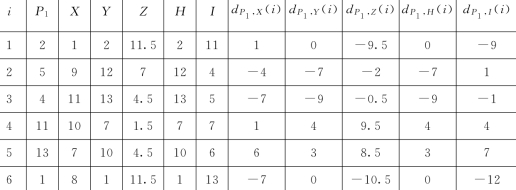
续表

计算皮尔曼等级相关系数见表10。

表10　江山市水权市场中的皮尔曼等级相关系数

显著水平α=0.05，样本容量n=13，则r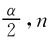=r0.025，13=0.5549。

结论：根据表9，江山市水权市场中，水资源价格P 1与水头Y、规模效应Z、水资源边际收益H、单位电能投资I表现出一定的相关性，与政策处理费用X表现出微弱相关性；其中与水头Y、水资源边际收益H相关性的程度相当；与政策处理费用X、水头Y、水资源边际收益H表现出正相关，与规模效应Z、单位电能投资I表现出负相关。

b.线性回归分析。使用Excel及Matlab软件计算以上统计量，得到表11，以及多元回归方程。

表11　线性回归统计量

各回归系数的t统计量为：

t=[-0.3375，-0.4755，-0.1415，0.4774，-0.1815]

五元线性回归方程为：

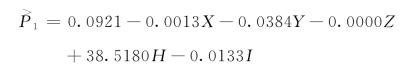
回归系数说明，每增加一个单位水资源边际效益，水资源价格就增加38.5180单位。从判定系数分析，各主要指标对水资源价格的影响中，只有15.10%可以被该五元线性回归方程解释，远小于1。

回归分析中，要求随机项均值为0，并服从正态分布。从统计量F分析，查表得F 0.05（5，7）=3.97，F=0.2490＜3.97，所以回归效果在水平α=0.05下不显著，即P 1与五个主要指标间没有显著的线性关系。从统计量t分析，γ=13-5-1=7，α=0.05，查表得t 0.05，7=2.365，所以各回归系数在水平α=0.05下不显著。因此，五元线性回归方程不合适。

3）遂昌县水权市场。

a.水权价格相关指标间的关系研究见表12。

表12　遂昌县水权市场中6个指标的等级数据

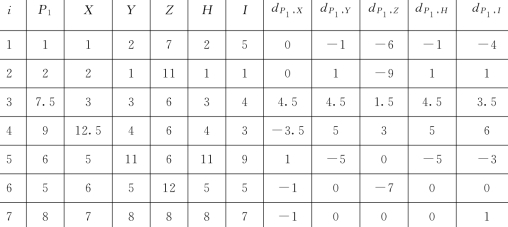
续表

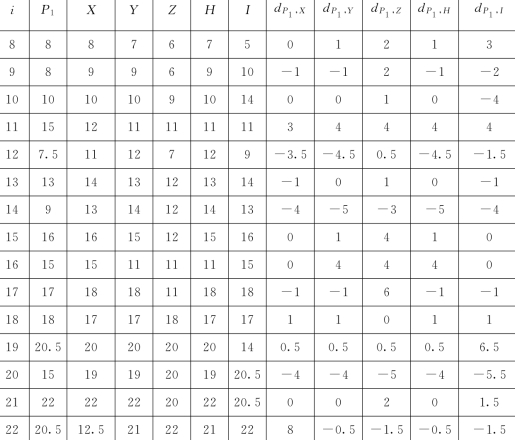
计算皮尔曼等级相关系数见表13。

表13　遂昌县水权市场中的皮尔曼等级相关系数

显著水平α=0.05，样本容量n=22，则r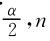=r0.025，22=0.4241。

结论：根据表13，在遂昌县水权市场中，水资源价格P 1与水头Y、水资源边际收益H表现出强相关性，与政策处理费用X表现出弱相关性，与规模效应Z、单位电能投资I几乎不相关，其中与水头Y、水资源边际收益H相关性的程度相当；与政策处理费用X、水头Y、水资源边际收益H表现出正相关。

b.线性回归分析。使用Excel及Matlab软件计算以上统计量，得到表14以及五元线性回归方程。

表14　线性回归统计量

各回归系数的t统计量为：

t=[0.4467，0.4252，-0.6411，-0.4177，1.2246]

五元线性回归方程为：

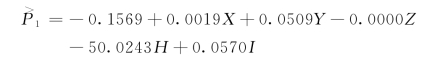
回归系数说明，每增加一个单位水资源边际效益，水资源价格就减少50.0243单位。从判定系数分析，各主要指标对水资源价格的影响中，有51.67%可以被该五元线性回归方程解释，与1相差较大。

回归分析中，要求随机项均值为0，并服从正态分布。从统计量F分析，查表得F 0.05（5，16）=2.85，F=3.4212＞2.85，回归效果在水平α=0.05下显著，即P 1与五个主要指标间的线性关系是显著的。因为R2=0.5167，所以五元线性回归拟合的效果不是很好，即五个主要指标对变量P1的解释能力不强。从统计量t分析，α=0.05，γ=22-5-1=16，查表得t0.05，16=2.120，所以各回归系数在水平α=0.05下都不显著。因此，五元线性回归方程不合适。

4）三个地区的综合水权市场。

a.水权价格相关指标间的关系研究见表15。

表15　综合水权市场中6个指标的等级数据

续表

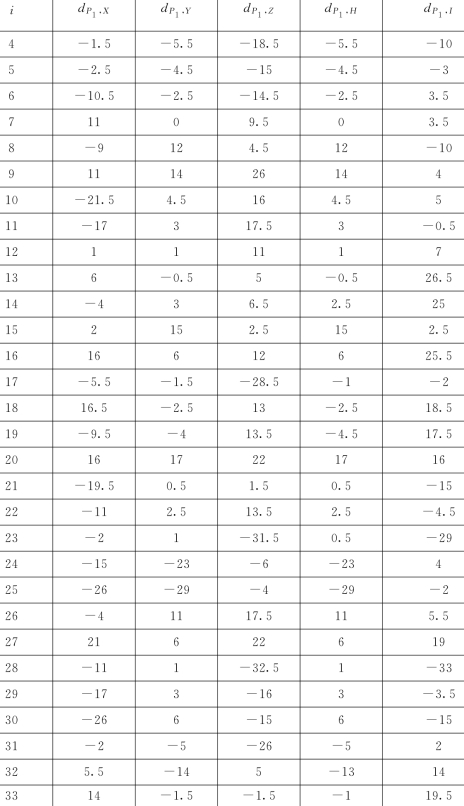
续表

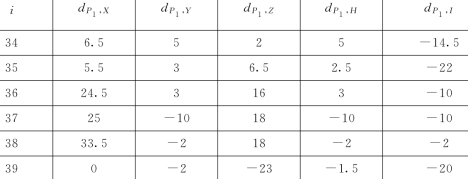
计算皮尔曼等级相关系数见表16。

表16　综合水权市场中的皮尔曼等级相关系数

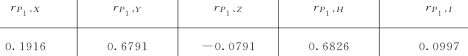
设显著水平α=0.05，样本容 量n=29，则=0.3180。

结论：根据表16，在三个地区的综合水权市场中，水资源价格P 1与水头Y、水资源边际收益H表现出强相关性，与政策处理费用X表现出弱相关性，与规模效应Z、单位电能投资I几乎不相关，其中与水资源边际收益H相关性的程度较与水头Y相关性略强一些；与政策处理费用X、水头Y、水资源边际收益H表现出正相关。(www.xing528.com)

b.线性回归分析。使用Excel及Matlab软件计算以上统计量，得到表17，以及多元线性回归方程。

表17　线性回归统计量

各回归系数的t统计量为：

t=[0.9831，0.4784，-0.2872，-0.4691，1.1774]

五元线性回归方程为：

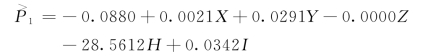
回归系数说明，每增加一个单位水资源边际效益，水资源价格就减少28.5612单位。从判定系数分析，各主要指标对水资源价格的影响中，有38.74%可以被该五元线性回归方程解释。

回归分析中，要求随机项均值为0，并服从正态分布。从统计量F分析，查表得2.45＜F 0.05（5，33）＜2.53，F=4.1738＞F 0.05（5，33），所以线性回归效果在水平α=0.05下显著，即P 1与五个主要指标间的线性关系是显著的。R 2=0.3847，所以五元线性回归的拟合的效果不是较差，即五个主要指标对变量P 1的解释能力较差。从统计量t分析，γ=39-5-1=33，α=0.05，查表2.021＜t 0.05，33＜2.042，所以各回归系数在水平α=0.05下不显著。因此，五元线性回归方程不合适。

（2）水权转让价格模型。该部分相关分析与线性回归分析的主要内容是研究4个主要指标P 2、X、Z、I间的相互关系问题。这些指标之间有无关系？若有关系，关系的紧密度如何？存在的是什么样的关系？通过以下分析，可以知道影响各地区水权转让价格的主要因素，以及变量间的变化趋势。

设r P2（i）、r X（i）、r Z（i）、r I（i）分别表示在第i个水站中P 1、X、Z、I样本数据的等级。

1）仙居县水权市场。

a.水权转让价格相关指标间的关系研究见表18。

计算皮尔曼等级相关系数见表19。

设显著水平α=0.10，样本容量n=4，则r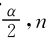=r0.05，4=0.8000。

结论：水权转让价格P 2与规模效应Z表现出强相关性，与政策处理费用X、单位电能投资I表现出弱相关性；与规模效应Z表现出正相关，与政策处理费用X、单位电能投资I表现出负相关。

表18　仙居县水权市场中4个指标的等级数据

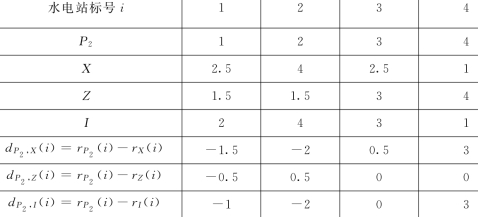
表19　仙居县水权市场中的皮尔曼等级相关系数

b.线性回归分析。线性回归分析是用线性函数关系近似描述相关关系的表现形式，反映各变量间的变化趋势或规律。

多元线性回归分析：

根据上述分析，P 2与X、Z、I间都表现出一定的相关性，所以建立下面的三元线性回归函数：

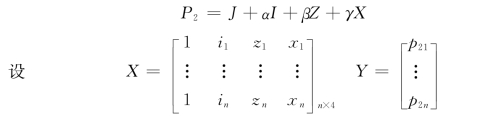
使用Excel及Matlab软件计算以上统计量，得到表20。

表20　线性回归统计量

各回归系数的t统计量为：

t=[0，0，0]

三元线性回归方程为：

从表20数据可以看出，F统计量为Na N说明回归效果非常差，t统计量为0说明回归系数的显著性很差。这是因为，在检验回归系数显著性的t检验中，自由度γ=n-p-1，而此处γ=4-3-1=0。所以，这里使用三元线性回归是不合适的。下面给出一元线性回归。

一元线性回归分析：

水权转让价格P 2与规模大小Z的一元线性回归函数为：

P 2=J+βZ

使用Excel及Matlab软件计算以上统计量，得到表21。

表21　线性回归统计量

回归系数的t统计量为：

t=2.5292

一元线性回归方程为：

回归系数说明，每增加一个单位水资源边际效益，水权转让价格增加0.1121单位。从判定系数分析，水资源边际效益对水资源价格的影响中，有76.18%可以被该一元线性回归方程解释。

回归分析中，要求随机项均值为0，并服从正态分布。从统计量F分 析，查 表 得F 0.05（1，2）=18.51，因 为F=6.3968＜18.51，所以回归效果在水平α=0.05下不显著。从统计量t分析，γ=4-1-1=2，α=0.05，查表得t0.05，2=4.303，所以各回归系数在水平α=0.05下不显著。因此，一元回归方程不合适。

二元线性回归分析：

水权转让价格P 2与规模大小Z、单位电能的投资I的一元线性回归函数为：

P 2=J+βZ+γI

使用Excel及Matlab软件计算以上统计量，得到表22。

表22　线性回归统计量

各回归系数的t统计量为：

t=[8.7927，15.1613]

二元线性回归方程为：

回归系数说明，规模大小每增加一个，水权转让价格增加103.4222个单位。从判定系数分析，水资源边际效益对水权转让价格的影响中，有99.70%可以被该二元线性回归方程解释。

回归分析中，要求随机项均值为0，并服从正态分布。从统计量F分析，查表得F 0.05（2，1）=199.50，因为F=163.8900＞199.50，所以回归效果在水平α=0.05下显著。R 2=0.9970，所以二元线性回归拟合的效果非常好，即Z、I对P 2的解释能力很强。从统计 量t分析，γ=4-2-1=1，α=0.05，查表得t 0.05，2=4.303，所以各回归系数在水平α=0.05下都显著，即Z、I对P 2有显著影响。

2）江山市水权市场。

a.水权转让价格相关指标间的关系研究见表23。

表23　江山市水权市场中6个指标的等级数据

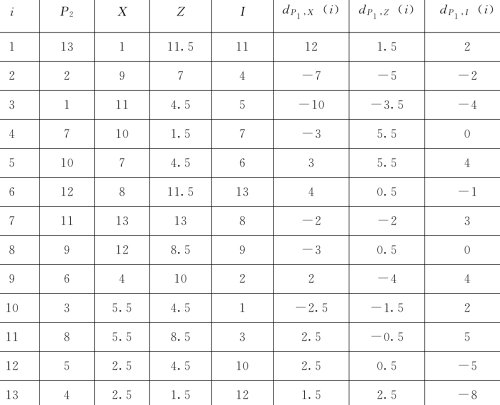
计算皮尔曼等级相关系数见表24。

表24　江山市水权市场中的皮尔曼等级相关系数

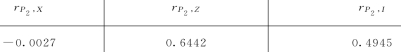
显著水平α=0.05，样本容量n=13，则r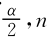=r0.025，13=0.5549。

结论：根据表24，江山市水权市场中，水权转让价格P 2与规模效应Z表现出强相关性，与单位电能投资I表现出弱相关性，与政策处理费用X几乎不相关；与规模效应Z、单位电能投资I表现出正相关。

b.线性回归分析。使用Excel及Matlab软件计算以上统计量，得到表25，以及三元线性回归方程。

表25　线性回归统计量

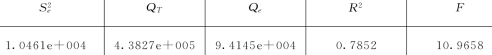
各回归系数的t统计量为：

t=[1.7111，4.2015，-1.6841]

三元线性回归方程为：

回归系数说明，每增加一个单位电能投资，水资源价格就增加137.4930个单位。从判定系数分析，各主要指标对水权转让价格的影响中，有78.52%可以被该三元线性回归方程解释。

回归分析中，要求随机项均值为0，并服从正态分布。从统计量F分析，查表得F 0.05（3，9）=3.86，因为F=10.9658＞3.86，所以回归效果在水平α=0.05下显著，即P 2与三个主要指标间的线性关系是显著的。R 2=0.7852，所以三元线性回归方程的拟合效果良好，即I、Z、X对P 2的解释能力良好。从统计量t分析，α=0.05，γ=13-3-1=9，查表得t0.05，9=2.262，所以Z的回归系数显著，I、X的回归系数在水平α=0.05下不显著。因此，Z对P 2有显著影响，I、X对P 2没有显著影响。

3）遂昌县水权市场。遂昌县水权市场等级数据见表26。a.水权价格相关指标间的关系研究。

表26　遂昌县水权市场中6个指标的等级数据

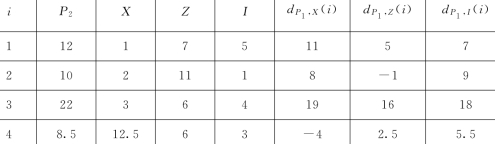
续表

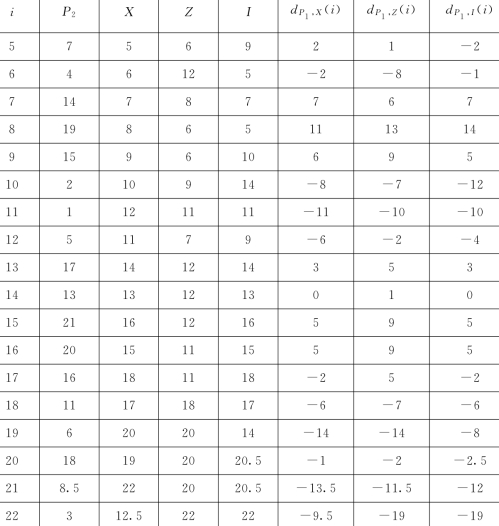
计算皮尔曼等级相关系数见表27。

表27　遂昌县水权市场中的皮尔曼等级相关系数

显著水平α=0.05，样本容量n=22，则r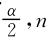=r0.025，13=0.4241。

结论：根据表27，水权转让价格P 2与规模效应Z表现出强相关性，与单位电能投资I表现出弱相关性，与政策处理费用X几乎不相关；与规模效应Z、单位电能投资I表现出正相关。b.线性回归分析。使用Excel及Matlab软件计算以上统计量，得到表28以及三元线性回归方程。

表28　线性回归统计量

各回归系数的t统计量为：

t=[1.0176，3.3687，1.1993]

三元线性回归方程为：

回归系数说明，每增加一个单位电能投资，水资源价格就增加52.7770个单位。从判定系数分析，各主要指标对水资源价格的影响中，有41.26%可以被该三元线性回归方程解释。

回归分析中，要求随机项均值为0，并服从正态分布。从统计量F分析，查表得F 0.05（3，18）=3.16，因为F=4.2153＞3.16，所以回归效果在水平α=0.05下显著，即P 2与三个主要指标间的线性关系是显著的。R 2=0.4126，相差1较大，所以I、Z、X对P 2的拟合效果不好，即I、Z、X对P 2的解释能力不强。从统计量t分析，α=0.05，γ=22-3-1=18，查表得t0.05，18=2.101，所以Z的回归系数显著，X、I的回归系数在水平α=0.05下不显著。因此，Z对P 2有显著影响，I、X对P 2没有显著影响。

4）三个地区的综合水权市场。三个地区的综合水权市场见表29。

a.水权转让价格相关指标间的关系研究。

表29　综合水权市场中指标的等级数据

续表

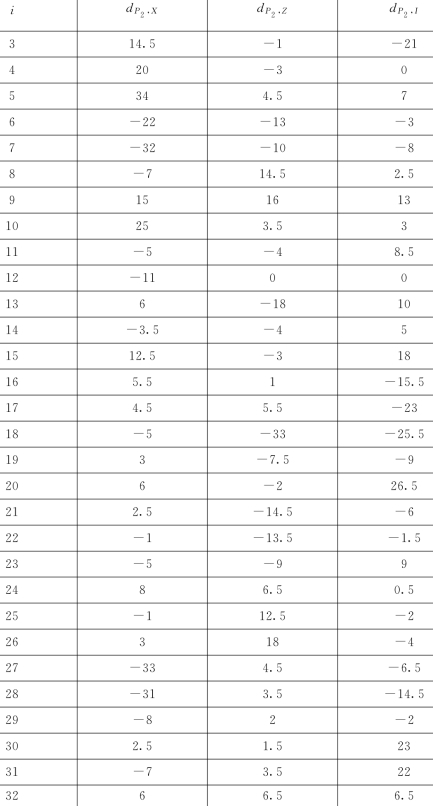
续表

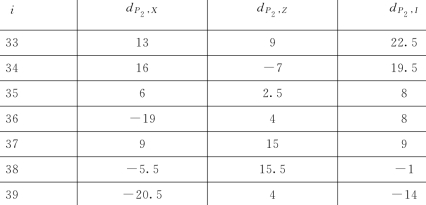
计算皮尔曼等级相关系数见表30。

表30　综合水权市场中的皮尔曼等级相关系数

设显著水平α=0.05，样本容量n=39，则

结论：根据表30，在三个地区的综合水权市场中，水权转让价格P 2与规模效应Z表现出强相关性，与单位电能投资I、政策处理费用X表现出微弱相关性；与政策处理费用X、规模效应Z、单位电能投资I都表现出正相关性。

b.线性回归分析。使用Excel及Matlab软件计算以上统计量，得到表31，及三元线性回归方程。

表31　线性回归统计量

各回归系数的t统计量为：

t=[1.7091，5.6862，0.6637]

三元线性回归方程为：

回归系数说明，每增加一个单位电能投资，水权转让价格就增加66.4700个单位。从判定系数分析，各主要指标对水权转让价格的影响中，有50.76%可以被该三元线性回归方程解释。

回归分析中，要求随机项均值为0，并服从正态分布。从统计量F分析，查表得2.84＜F 0.05（3，35）＜2.92，F=12.0267＞2.92，所以回归效果在水平α=0.05下显著，即P 2与三个主要指标间的线性关系是显著的。R 2=0.5076，相差1较大，所以I、Z、X对P 2的拟合效果不很好，即I、Z、X对P 2的解释能力不强。从统计量t分析，γ=39-3-1=35，α=0.05，查表得2.021＜t0.05，35＜2.042，所以Z的回归系数显著，X、I的回归系数在水平α=0.05下不显著。因此，Z对P 2有显著影响，I、X对P 2没有显著影响。