希尔伯特变换：保持能量不变的频谱分析方法

1.希尔伯特(Hilbert)变换的定义

希尔伯特交换简称希氏变换。对于一个实函数f(t),称为f(t)的希尔伯特变换,记作

称为g(t)的希尔伯特反变换,记作

可以证明

显然,希尔伯特变换可记为卷积形式

2.频域的变换

由式(B.4)可以看出,函数f(t)的希尔伯特变换可以看成是函数f(t)通过一个单位冲激响应为h(t)=的线性系统的输出,如图B.1所示。

图B.1　希尔伯特变换的等效

下面求函数f(t)的频谱H(ω)。为此,可以先求频率符号函数的傅里叶反变换。频率符号函数定义为

也可以表示为

式中,U(ω)=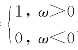为单位阶跃函数。频率符号函数的傅里叶反变换可表示为

即

由此得到

因此,函数f(t)的频谱H(ω)为

由于,所以希尔伯特变换实际上可以等效成一个理想相移器,即在ω＞0域相移,在ω＜0域相移

同样可以得到

由式(B.6)可以看出希尔伯特反变换也可以等效成一个相移器,在ω＞0域相移在ω＜0域相移

3.希尔伯特变换的性质(www.xing528.com)

(1)

证

因为H1(ω)H2(ω)=[-jsgnω][jsgnω]=1。

(2)

因为H1(ω)H1(ω)=[-jsgnω]2=-1。

(3)

证 令,则有

又知=-jsgnωF(ω),由此有,这表明函数f(t)的希尔伯特变换前与变换后的能量保持不变。

(4)若f(t)为偶函数,则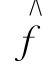(t)为奇函数;若f(t)为奇函数,则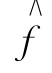(t)为偶函数。

证 令f(t)为偶函数,则有f(-t)=f(t)。根据定义:

令τ′=-τ,则

由此得证。

同理可证明第二个结论。

(5)

即f(t)与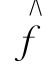(t)相互正交。利用性质4即可证明。

4.常用希尔伯特变换对