网格编码调制原理及应用技术

在传统的数字传输系统中,纠错编码与调制是各自独立设计并实现的,译码和解调也是如此。纠错编码需要冗余度,编码增益是依靠降低信息传输率来获得的。在功率受限信道中,功率利用率可以用频带利用率换取。在限带信道中,则可通过加大调制信号集来为纠错编码提供所需的冗余度,以避免信息传输速率因增加纠错编码而降低。因此,既希望能提高频带利用率,又希望在不增加信道传输带宽的前提下降低差错率。但若调制和编码仍按传统的相互独立的方法设计,则不能得到令人满意的结果。为了解决这个问题,近些年来发展起来了网格编码调制(TrellisCodedModulation,TCM)技术。它是利用编码效率为n/(n+1)的卷积码,并将每一码段映射为2n+1个调制信号集中的一个信号。在接收端信号解调后经反映射变换为卷积码,再送入维特比译码器译码。它有两个基本特点:

(1)在信号空间中的信号点数目比无编码的调制情况下对应的信号点数目要多,这些增加的信号点使编码有了冗余,而不牺牲带宽。

(2)采用卷积码的编码规则,使信号点之间引入相互依赖关系。仅有某些信号点图样或序列是允许用的信号序列,并可模型化成为网格状结构,因此又称为“格状”编码。

在信号星座图中,通常把信号点的几何距离称为欧几里德距离,简称欧氏距离。其中最短距离称为最小欧氏距离。当编码调制后的信号序列经过一个加性高斯白噪声的信道以后,在接收端采用最大似然解调和译码,用维持比算法寻找最佳格状路径,以最小欧氏距离为准则,解出接收的信号序列。这与卷积码维持比译码采用的汉明距离不一样。

一般TCM最优码是按照编码信号的网格图确定的。当一个TCM最优码确定后,其相应编码调制器的实现有两种方法,其一是先确定从编码符号到调制信号的映射函数,再根据网格图设计出相应的纠错编码器;另一个是先确定编码器结构,再根据网格图确定编码符号到调制信号的映射函数。

在设计和选择TCM最优码方案的网格图结构时,赋予信号的网格转移一种特性,即TCM方案通过一种特殊的信号映射可变成卷积码的形式。这种映射的原理是将调制信号集分割成子集,使得子集内的信号间具有更大的空间距离。

TCM的设计就是寻找与各种调制方式相对应的卷积码,当卷积码的每个分支与信号点映射后,使得每条信号路径之间有最大的欧氏距离。根据这个目标,对于多电平与多相位的二维信号空间,把信号点集不断地分解为2、4、8、…个子集,使它们中信号点的最小欧氏距离不断增大,这种映射规则称为集合划分映射。

图10.7.1给出了一种8PSK信号空间的集合划分,所有8个信号点分布在一个圆周上,都具有单位能量。连续3次划分后,分别产生2、4、8个子集,最小欧氏距离逐次增大,即

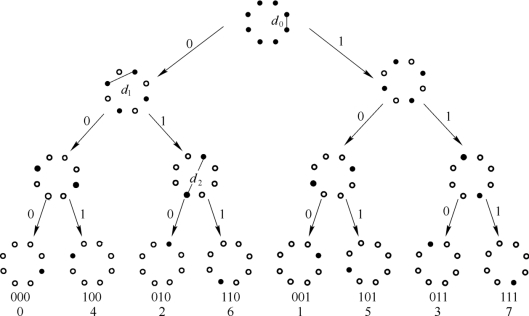
图10.7.1　8PSK信号空间的集合划分(www.xing528.com)

可以得到TCM编码调制器的系统方框图,如图10.7.2所示。

图10.7.2　TCM编码调制器的系统方框图

设输入码字有n比特,在采用多电平与多相位调制时,有同相分量和正交分量,因此在无编码的调制时,在二维信号空间中应有2n个信号点与它对应。在应用编码调制时,为增加冗余度,有2n+1个信号点。在图10.7.1中,可划分为4个子集,对应于码字的1bit加到编码效率为1/2的卷积码编码器输入端,输出2bit,选择相应的子集。码字的剩余的未编码数据比特确定信号与子集中信号点之间的映射关系。

在接收端采用维特比算法执行最大似然检测。编码网格状图中的每一条支路对应于一个子集,而不是一个信号点。检测的第一步是确定每个子集中的信号点,在欧氏距离意义下,这个子集是最靠近接收信号的子集。

图10.7.3(a)描述了最简单的传输2bit码字的8PSKTCM编码方案。它采用了效率为1/2的卷积码编码器,对应的网格图如图10.7.3(b)所示。该结构有4个状态,每个状态对应于图10.7.1中距离为d2的4个子集。

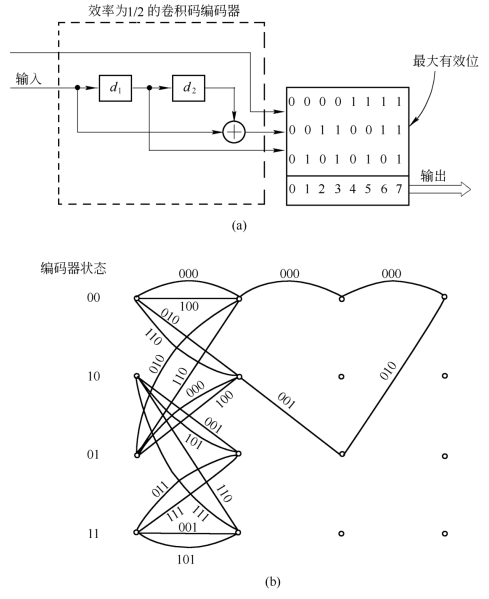
图10.7.3　传输2bit码字的8PSKTCM编码方案

通常,TCM方案的最优码是通过手算或计算机搜索的方法获得的。对一些状态数较小的常见TCM码,人们已找出了其最优码。