系统循环码的编译码技巧

1.系统循环码的编码

对于码组前k位是信息码元的系统码,用多项式表示则为

式中,m(x)是不大于k-1次的多项式,代表信息码元;r(x)是不大于r-1次的多项式,代表监督码元。

若令式(10.4.6)中的信息码元为m′(x),则码组多项式可写成

联立式(10.4.26)和式(10.4.27)得

即

这就是循环码编码的数学依据,式中m′(x)为商,r(x)为余式。

利用生成多项式g(x)作除法运算的循环码编码方法归纳如下:

(1)信息多项式m(x)左移n-k位,即相当于m(x)乘因子xn-k;

(2)以g(x)为除式作模运算,得余式r(x),即

(3)余式的系数作监督码元,附加在信息码元之后形成系统码,相当于令余式r(x)和已经左移n-k位的信息码多项式作按位模2加运算,即

例10.4.2 已知(7,4)系统循环码的生成多项式为g(x)=x3+x2+1,若信息码为1001,求编码后的循环码组。

解 信息码多项式为m(x)=x3+1,由式(10.4.28)可得

可见r(x)=x+1,因此由(10.4.30)得(www.xing528.com)

其对应的码组为1001011。

以上编码方法的实现电路并不复杂,多项式除法可以用带反馈的线性移位寄存器来实现。有两种不同的除法电路即采用“内接”的模2和(异或门)电路与采用“外接”的模2和电路,生成多项式为g(x)=x6+x5+x4+x3+1的两种除法电路如图10.4.2中(a)(b)所示,一般多采用内接模2和的除法电路。内接模2和除法电路的工作过程与采用手算进行长除的过程完全一致。

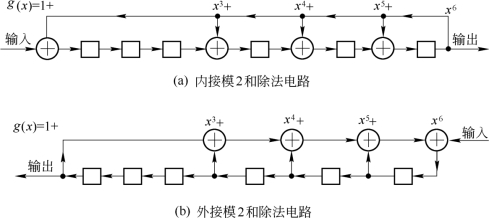
图10.4.2　两种除法电路

2.系统循环码的译码

设发送码组为A、接收码组是B,如果对译码电路只要求检错不纠错,那么将式(10.4.27)改为

以式(10.4.31)为依据,接收机译码器用g(x)除接收码组B(x),若余数为0则B=A,否则表示B中有错,需发重传指令。利用除法电路实现的检错译码器原理框图如图10.4.3所示(图中除法电路与编码器中的除法电路相同)。

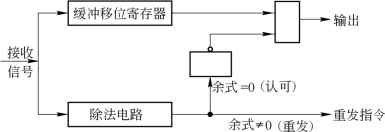
图10.4.3　检错译码器原理框图

为纠错而采用的译码方法比较复杂。循环码的译码步骤如下:

(1)由接收码组B计算S;

(2)由校正子S确定错误图样E;

(3)将错误图样E与接收码组B模2加,即纠正错误。

由式(10.3.18)、式(10.3.19)可知

对于循环码而言,校正子多项式

即用接收码多项式除以生成多项式g(x)得到的余式,就是循环码的校正子多项式S(x),这就大大简化了校正子的计算。同时,由于循环码的校正子多项式S(x)与循环码组一样也具有循环移位特性(某码组循环移位i次的校正子,等于原码组校正子在除法电路中循环移位i次所得到的结果)。因此,对于只纠一位错误码元的译码器,可以针对接收码组中单个错误出现在首位的错误图样及其相应的校正子来设计组合逻辑电路;然后利用除法电路中移位寄存器的循环移位去纠正任何位置上的单个错误。这种基于错误图样识别的译码器称为梅吉特译码器。