汉明码及其电路设计与优化

汉明码是一种可以纠正单个随机错误的线性分组码。它的最小码距dmin=3,监督码元位数r=n-k(r是一个大于或等于2的正整数),码长n=2r-1,信息码元位数k=2r-1-r。编码效率R=k/n=(2r-1-r)/(2r-1)=1-r/(2r-1)。当r很大时,R的极限趋于1,所以是一种高效码。

汉明码的监督矩阵H有n列r行,它的n列由不全为0的二进制r位码的不同组合构成,即每种组合只在某列中出现一次。以r=3为例,它的码长n=23-1=7,所以前面所说的(7,4)线性分组码就是汉明码,并且任意调换H矩阵中各列的位置,不会影响码的纠、检错能力。例如,可以构造出与式(10.3.9)不同的监督矩阵,即

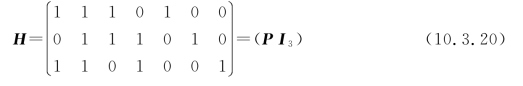
其相应的生成矩阵为

因此,汉明码H矩阵中各列的位置还可以有其他多种排列形式。

汉明码的译码方法可以采用计算校正子,然后确定错误图样并加以纠正的方法。图10.3.1中给出了式(10.3.20)所示(7,4)汉明码的编码器和译码器电路图。(www.xing528.com)

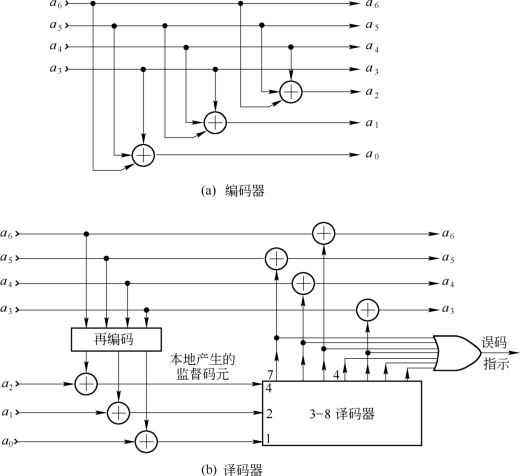
图10.3.1　(7,4)汉明码的编码器和译码器电路图

纠正单个错误的汉明码中,r位校正子码组与误码图样一一对应,最充分地利用了监督位所能提供的信息,这种码称为完备码。在一般情况下,对于能纠正t个错误的线性分组码(n,k),应满足不等式

式中,Cin为n中取i的组合,其物理意义是n位码组中有i个误码的错误图样数目(i≠0)。式(10.3.22)取等号时,校正子与误码不超过t个的所有错误图样一一对应,监督码元得到最充分的利用,这种(n,k)码即为完备码。

除汉明码外,迄今为止已找到的唯一能纠正多个错误的完备码是(23,12)非本原BCH码,常称为戈雷(Golay)码。