监督矩阵与生成矩阵简介

1.监督矩阵H

改写式(10.3.1)所示(7,4)线性分组码的3个线性方程式

写成矩阵形式为

或

分别记作

或

式中,是r×n阶矩阵,称为线性分组码的一致监督矩阵(或校验矩阵);

AT、0T、HT分别是矩阵A、0、H的转置。

对于码字A来说,恒有

或

(www.xing528.com)

成立,即当监督矩阵H给定时,利用式(10.3.7)可以验证接收码是否正确。

H矩阵可以分成两部分:

式中,P为r×k阶矩阵,Ir为r×r阶单位方阵,具有(PIr)形式的H矩阵称为典型矩阵。由线性代数的基本理论可知,监督矩阵各行一定是线性无关的,否则不可能得到r个独立的监督位。非典型形式的监督矩阵可以经过线性变换化为典型形式。

2.生成矩阵G

改写式(10.3.1)为矩阵形式,有

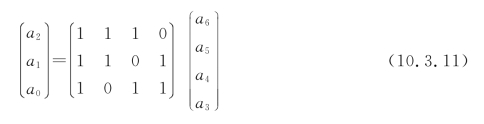
或者

式中,Q为k×r阶矩阵。该式表明,已知Q矩阵,同样可以由信息位算出监督码元。不难看出,Q是P的转置,即

如果在Q的左边放上一个k×k阶单位方阵,就构成了生成矩阵

称G为生成矩阵,是因为利用它可以产生码组A,即

符合(IkQ)形式的生成矩阵称为典型形式的生成矩阵,由该矩阵得到的码组是系统码。利用此生成矩阵同样可以得到表10.3.1中给出的(7,4)线性分组码的全部码字。

同样,生成矩阵的各行也必定是线性无关的,每行都是一个许用码组,k行许用码组经过行运算可以生成2k个不同的许用码组。非典型形式的生成矩阵经过运算也一定可以化为典型形式。若生成矩阵各行中有线性相关的,则不可能由其生成2k种不同码组。

典型监督矩阵和典型生成矩阵之间存在以下关系: