基本概念解析

一个长为n的分组码,码字由两部分构成,即信息码元(k位)+监督码元(r位)。监督码元是根据一定规则由信息码元变换得到的,变换规则不同就构成不同的分组码。如果监督位为信息位的线性组合,则称其为线性分组码。

要从k个信息码元中求出r个监督码元,必须有r个独立的线性方程。根据不同的线性方程,可得到不同的(n,k)线性分组码。

例如,已知一个(7,4)线性分组码,4个信息码元a6、a5、a4、a3和3个监督码元a2、a1、a0之间符合以下规则

计算式(10.3.1)得到此(7,4)线性分组码的全部码组,列于表10.3.1中(许用码组的个数等于k个信息码元的全部组合数2k个)。

表10.3.1　(7,4)线性分组码的全部码组

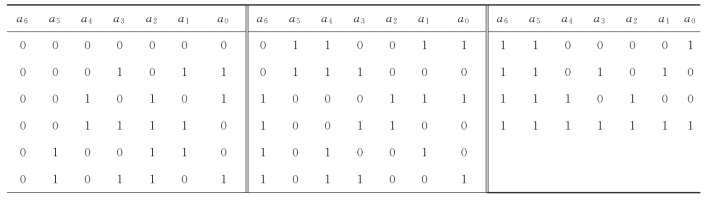
奇偶监督码是一种最简单的线性码。改写式(10.2.5)、式(10.2.6)可以得到监督码元a0和信息码元之间的关系。

奇校验(www.xing528.com)

偶校验

线性码各许用码组的集合构成了代数学中的群,因此又称为群码。它有如下性质:

(1)任意两许用码组之和(按位模2加)仍为一许用码组,即线性码具有封闭性。

(2)集合中的最小距离等于码组中非全“0”码字的最小重量。

在群中只存在一种运算,即模2加,通常四则运算中的加、减法在这里都是模2加的关系。所以后面将运算符号⊕简化为“+”。

为了说明(n,k)线性分组码的编码原理,下面引入监督矩阵H和生成矩阵G的概念。