帧同步性能优化探究

帧同步系统的性能指标有漏同步概率P1、假同步概率P2、帧同步平均建立时间ts等。一般要求系统的同步建立时间要短,漏同步概率P1和假同步概率P2要小。但是,要达到三项指标都小是不可能的,通过分析,可以看出它们之间是互相矛盾的。下面主要以连贯式插入法为例,说明帧同步性能指标的计算。

1.漏同步概率P1

在通信系统中,由于噪声和干扰的影响,会引起帧同步码组中一些码元发生错误,从而识别器会漏识已发出的帧同步码组,出现这种情况的概率称为漏同步概率,用符号P1表示。仍然以7位巴克码识别器为例,设判决门限为6,此时7位巴克码中只要有一位码发生错码,7位巴克码全部进入识别器时加法器的输出电平会由7变为5,此时就会出现漏同步,只有一位码都不发生错误时,才不会出现漏同步。

假设数字通信系统的误码率为P,7位码中一个码元都不错的概率为(1-P)7,因此判决门限电平为6时漏同步概率为P1=1-(1-P)7。如果为了减少漏同步,判决门限改为4,此时容许在帧同步码组中有一个错码,则出现一个错码的概率为C17P1(1-P)7-1,漏同步概率为P1=1-[(1-P)7+C17P1(1-P)7-1]。

如果设帧同步码组的码元数目为n,判决器允许帧同步码组中最大错码数为m,则漏同步概率P1的一般表达式为

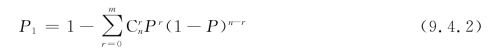
例如,7位巴克码识别器,系统误码率为1/1000,在m=0和1时,漏同步概率P1分别为

当m=0时,

当m=1时,

2.假同步概率P2(www.xing528.com)

在信息码元中,自然也可能会出现与所要识别的帧同步码组相同的码组,这时识别器会把它误认为是帧同步码组而出现假同步。发生这种情况的概率称为假同步概率,用符号P2表示。

假同步概率P2的计算,可以通过计算信息码元中能被判为同步码组的组合数与所有可能的码组数之比来获得。设二进制信息码中1、0码等概率出现,P(0)=P(1)=0.5,则由该二进制码元组成n位码组的所有可能的码组数为2n个,而其中能被判为同步码组的组合数也与判决器允许帧同步码组中最大错码数m有关。若m=0,则只有C0n个码组能识别;若m=1,则有C0n+C1n个码组能识别。依此类推,信息码中可被判为同步码组的组合数为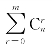,由此得到假同步概率的一般表达式为

例如,7位巴克码识别器n=7,在判决器允许帧同步码组中最大错码数m=0和1时,假同步误码率分别为

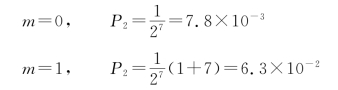
从式(9.4.2)和式(9.4.3)以及例题可以看出,当判决器允许帧同步码组中最大错码数m增大时,P1下降,而P2增大,显然二者是矛盾的;另外还可以看出,当巴克码组数n变大时,P1增大,而P2下降,二者也是矛盾的。因此对m和n的选择要兼顾对P1、P2的要求。

3.平均同步建立时间ts

在连贯式插入法实现帧同步的情况下,设一帧的码元数为N,帧同步码组长为n,码元时间间隔为Tb。假设漏同步和假同步都不发生,即P1=0,P2=0,在最不利的情况下,实现帧同步最多需要一帧的时间,则最长的帧同步时间为NTb。考虑到出现漏同步或假同步时要多花费同步建立的时间,因此,帧同步的平均建立时间近似为

在间歇式插入法中采用逐码移位法实现帧同步时,从帧同步建立的原理来看,如果信息码中所有的码都与帧码不同,那么最多只要连续经过N次调整,经过NTb的时间就可以建立同步。但实际上信息码中“1”“0”码均会出现,当出现“1”码时,例如上面帧同步过程举的例子,第1个位同步码对应的时间内信息码为“1”,图9.4.8中异或门输出c⊕d=0,e=0,f=0,禁门不起作用,不扣除第2位同步码。因此,本地帧码不会右移展宽,这一帧调整不起作用,一直要到下一帧才有可能调整。假如下一帧本地帧码d还是与信码中“1”码相对应,则调整又不起作用。当信息码中“1”“0”码等概率出现时,即P(1)=P(0)=0.5时,经过计算,帧同步平均建立的时间近似为