如何非均匀量化？

在均匀量化中,量化误差与被量化信号电平大小无关。量化误差的最大瞬时值等于量化间隔的一半,所以信号电平越低,信噪比越小。例如,量化间隔为0.1V时,最大量化误差是0.05V。信号幅度为5V时,量化误差为信号幅度的0.05/5=1%;信号幅度为0.5V时,量化误差就达到信号幅度的0.05/0.5=10%。

为了解决上述问题,可以考虑让量化间隔的大小随输入信号电平的大小而改变。在被量化信号小时,让量化间隔小,则量化误差也小;在被量化信号大时,让量化间隔大,则量化误差就大。但不论在何时,量化信噪比基本保持不变,且满足要求,与此同时,量化级数也未增加,这就是非均匀量化的思路。

1.压扩特性

在实践中,人们利用压扩技术来实现非均匀量化。在发送端首先让输入信号通过一个具有如图8.3.7(a)所示的压缩特性的部件,然后再进行均匀量化和编码。在接收端利用图8.3.7(b)所示的扩张器来完成相反的操作,使压缩后的波形复原。压缩和扩张特性分别具有把信号幅度范围压缩与扩张的作用,只要压缩和扩张特性恰好相反,则压扩过程就不会引起失真。压缩器和扩张器合在一起称为压扩器。为了简化,图8.3.7所示的压缩和扩张特性通常只画出第一象限的图形。

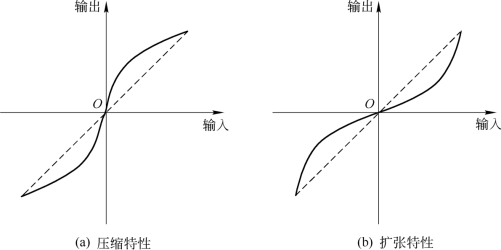
图8.3.7　压缩和扩张特性

为了进一步理解压扩技术的基本过程,图8.3.8(a)画出了采用压扩技术的系统框图,图8.3.8(b)画出了非均匀量化原理示意图。

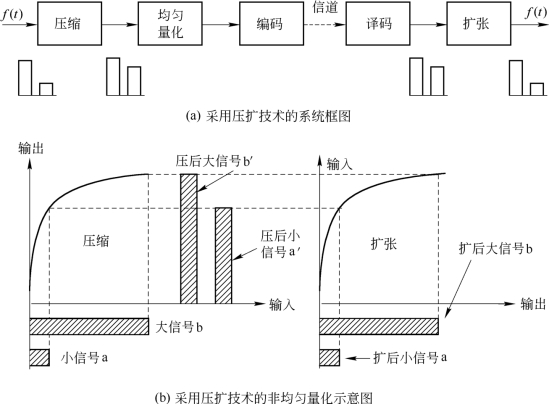
图8.3.8　采用压扩技术的系统框图和量化示意图

在图8.3.8中,发送端依次输入了一个小信号a和一个大信号b,信号经过压缩器后,对小信号a进行了较大的放大成为a′,对大信号b进行压缩变成了b′。由于小信号的幅度得到较大的放大,从而使小信号的信噪比大为改善,这就相当于把信号的动态范围展宽了,经此压缩处理之后,再进行均匀量化、编码,送入信道传输。在接收端,译码后输出的信号分别是a′、b′,它们经过具有与发送端压缩特性相反的扩张特性的扩张器,将其恢复成原来输入的信号a和b。可直观地看出:非均匀量化是以牺牲大信号的信噪比来改善小信号的信噪比。

动态范围可定义为满足信噪比要求的输入信号的取值范围。图8.3.9给出了没有压缩处理和经压缩处理后的信噪比随信号变化的曲线示意图。从图中可以看出,在7位编码时,没有进行压缩处理的输入信号需要大于-18dB左右才能满足信噪比大于26dB的要求;经压扩后,输入信号只要大于-38dB左右就能满足信噪比大于26dB的要求。这相当于信号动态范围提高了近20dB。同时还可以看出,采用压扩技术后,只用7位编码就能把小信号的量化噪声控制在11位编码相同的水平上。

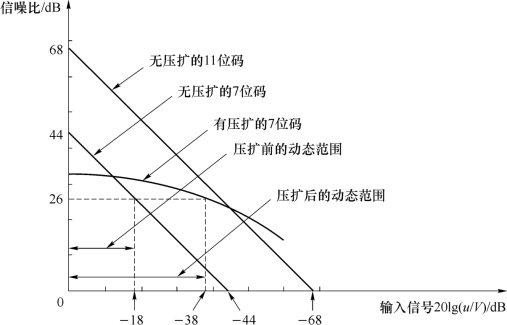
图8.3.9　无压缩和有压缩信噪比随信号变化的比较曲线

2.实际中采用的两种压扩特性

压扩特性的选择与信号的统计特性有关。理论上,具有不同概率分布的信号都有其相对应的最佳压扩特性,使量化噪声达到最小。但是在实际中还应考虑压扩特性易于在电路中实现以及压扩特性的稳定性等问题。例如:人们曾经应用和建议试用过的特性就有对数特性、指数特性、双曲线特性和改进型双曲线特性等。对于语音信号来说,在实际中常用对数压扩特性,但对数曲线在自变量趋于零时,函数趋于无穷大,这显然是不满足要求的,为此需要修正对数曲线,以使其满足在输入为零时,压扩的输出也为零,实际中采用的修正方法有两种,分别被称为μ律和A律压扩特性,它们接近于最佳的压扩特性,并且易于进行二进制编码。下面分别给出归一化的μ律和A律特性。

(1)归一化的μ律压缩特性

(www.xing528.com)

式中,x和y分别是归一化的压缩器输入和输出电压。假设输入信号u和输出信号v的最大取值范围是-V～V,则归一化后,x=u/V,y=v/V。μ为压扩参数,表示压扩程度,μ越大,压缩效果越明显。μ=0对应于均匀量化,无压扩,一般取μ=100左右,也有用μ=255的。μ特性在小输入电平时,即当μ|x|≪1时,近似于线性;而在大输入电平时,即μ|x|≫1时,它的特性近似对数关系。μ律压缩特性如图8.3.10(a)所示,且满足奇对称,图中只画了第一象限的图形。

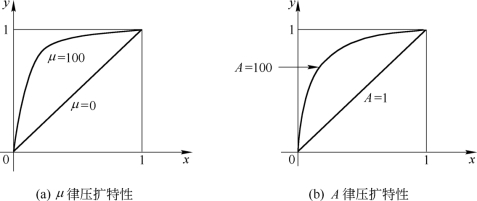
图8.3.10　压缩特性

(2)归一化的A律压缩特性

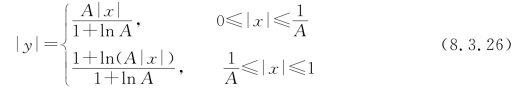
式中,x和y的含义与μ律相同;A是压扩参数,表示压扩的程度,A越大,压缩的效果越明显。A的取值一般也在100左右,A=1时对应着不压缩的均匀量化。显然,A律压缩特性是分段定义的,当1/A≤|x|≤1时是对数曲线;当0≤|x|≤1/A时是过原点的直线,该直线是后半段对数曲线的切线,切点在A律压缩特性如图8.3.10(b)所示,且满足奇对称。

(3)非均匀量化的量化噪声功率

当量化级数m较大时,非均匀量化间隔的大小如图8.3.11所示,约为

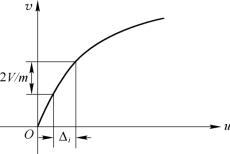
图8.3.11　没有归一化的压缩特性

由式(8.3.27)、式(8.3.7)、式(8.3.10),以及各量化电平上的量化噪声可以近似地认为在量化间隔范围内均匀分布等条件,非均匀量化未过载的量化噪声功率可近似地表示为

式中,p(u)为输入信号的概率密度。对于语音信号,其概率密度可用式(8.3.5)及图8.3.4所示的指数函数来近似。

称为非均匀量化对均匀量化噪声的改善系数。从式(8.3.28)和(8.3.12)可以看出,非均匀量化的量化噪声功率是均匀量化噪声功率与改善系数之积,dv/du=dy/dx越大,β越小,非均匀量化的量化噪声功率Nq就越小,对量化噪声的改善越好。