二进制最佳接收优化提升接收性能

匹配滤波器最佳接收机(如图7.4.1(a)所示)和相关最佳接收机(如图7.4.1(b)所示)两者是等效的,这里取k=1。下面从匹配滤波器接收机的角度来讨论二进制最佳接收机的接收性能。

接收端收到的信号为y(t)=si(t)+n(t),i=1,2,其中si(t)(i=1,2)是发送信号,n(t)是信道上产生的加性零均值高斯白噪声。单边功率谱密度函数为n0,匹配滤波器的单位冲激响应为h(t)↔H(ω),匹配滤波器最佳接收机框图如图7.4.1(a)所示。

图7.4.1　二进制最佳接收机

显然,抽样判决的最佳时刻为t0=T,T是码元周期。此时的抽样值为

由高斯过程的性质可知,y0(T)是一高斯随机变量,均值为

方差为

式(7.4.4)用到帕斯瓦尔定理:

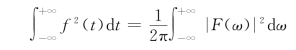
接收电路依据y0(T)判决,它等效于依据最大似然函数判决(设发送端等概率发送信号s1(t)、s2(t),即P(s1)=P(s2)),因此有

其中,似然函数分别为

将式(7.4.6)代入式(7.4.5),且设m2＞m1,经整理可得

因此,二进制最佳接收的平均误码率为

将P(s1)=P(s2)=1/2代入式(7.4.8),同时将式(7.4.6)代入式(7.4.8),经推导有

式中,Q函数的定义如下(见附录C):

(www.xing528.com)

整理式(7.4.9)可得

式(7.4.11)说明,二进制最佳接收的平均误码率Pe取决于归一化距离

d越大,平均误码率Pe越小。

将式(7.4.2)、式(7.4.3)、式(7.4.4)代入式(7.4.12),再平方得

利用施瓦兹不等式,当

时,d2达到最大,为

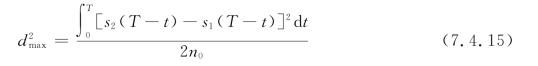
整理式(7.4.15)的分子,得

式中,

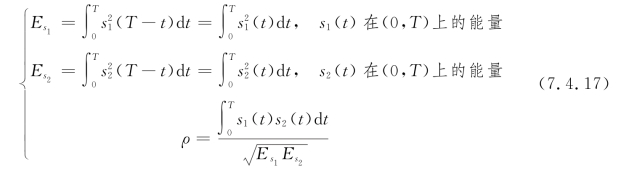
式中,ρ称为s1(t)、s2(t)两波形的波形系数,在[-1,1]内取值,它反映了这两个波形的相似程度。

先将式(7.4.16)代入式(7.4.15),然后再将式(7.4.15)代入式(7.4.11),由此得到二进制最佳接收的平均错误概率为

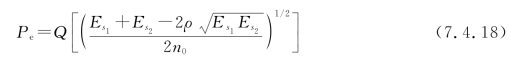
当Es1=Es2=E时,式(7.4.18)可以简化为

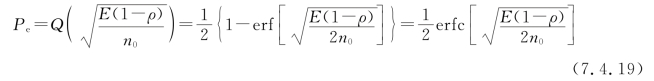
式中,erf(x)是误差函数,erfc(x)是误差互补函数(见附录C)。

式(7.4.19)说明,错误概率Pe与信号的能量E、噪声n0和信号的相关系数ρ有关,当信号的能量E和噪声n0一定时,错误概率Pe随信号的相关系数ρ增大而增大。ρ的取值范围是[-1,1],因此,ρ=-1时,Pe最小;ρ=1时,Pe=1/2最大,此时,系统无法正常工作。