1.给出设计任务
假设发送的确知信号为s(t),它是(0,T)上的时间受限信号;信号在信道上受到加性白噪声n(t)的干扰,它的双边功率谱密度函数是n0/2。下面要求设计一个线性滤波器,使输出的有用信号在某一时刻达到最大,以便在该时刻抽样后正确地判决所发送的信号,实现正确接收。接收系统的原理框图如图7.3.1所示。
依据设计任务的要求,用最大的输出信噪比作为判决准则。而理论和实践也都证明了在白噪声干扰下,如果线性滤波器的输出端在某时刻t0使信号的瞬时功率与噪声的平均功率之比最大,就可以使判决电路产生错误判决的概率极小。称这样的线性滤波器为
图7.3.1 接收系统的原理框图
满足最大输出信噪比准则的最佳线性滤波器。
(1)最大输出信噪比准则下的最佳线性滤波器的传递函数
设线性滤波器的单位冲激响应是h(t),其传递函数H(ω)↔h(t)。接收机收到的信号y(t)是发送信号s(t)↔S(ω)和白噪声n(t)的叠加,即
由图7.3.1可知,接收信号y(t)就是线性滤波器的输入信号。
因此,线性滤波器的输出信号为
式中,输出的有用信号为
线性滤波器输出噪声的平均功率为
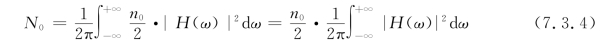
下面求在t0时刻线性滤波器的输出信噪比:
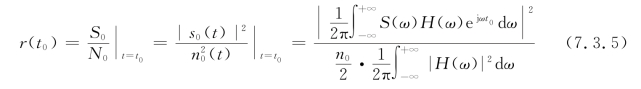
仔细研究式(7.3.5),发现信噪比r(t0)与线性滤波器的传递函数H(ω)有关系,如果能找到使r(t0)最大的H(ω),则就找到了要设计的滤波器。
在此引入施瓦兹不等式,
当X(ω)=KY*(ω)时,等号成立,其中K为常数,“*”表示共轭。
将施瓦兹不等式代入式(7.3.5),其中,X(ω)=H(ω),Y(ω)=S(ω)ejωt0,得
式中,
|S(ω)|2dω是所发送的有用信号的能量。
由式(7.3.6)可以看出,线性滤波器在t=t0时刻存在最大的输出信噪比,最大可以达到r(t0)|max=
,且达到这个最大信噪比的条件是
这就是最大输出信噪比准则下的最佳线性滤波器的传递函数。
结论:在加性白噪声信道干扰下,按照式(7.3.7)来设计的最佳线性滤波器,可使滤波器输出在t=t0时刻达到最大信噪比2E/n0。
仔细观察式(7.3.7)可以发现,线性滤波器的传递函数H(ω)是所发送有用信号的共轭频谱的K倍,且附加有ωt0的相移。这种与发送信号间的关系称为“匹配”,因此,这样的最佳线性滤波器称为匹配滤波器。
(2)匹配滤波器的单位冲激响应h(t)(www.xing528.com)
由式(7.3.7)可以求出匹配滤波器的单位冲激响应
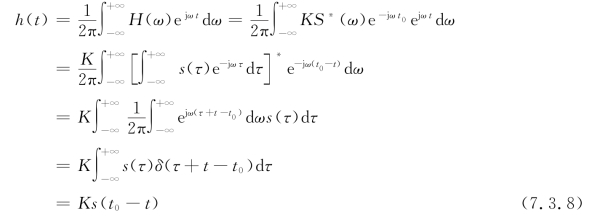
由此可以得出这样的结论:匹配滤波器的单位冲激响应h(t),等于发送信号s(t)先翻转s(-t),再向右平移t0的结果的K倍,即h(t)=Ks(t0-t),如图7.3.2所示。
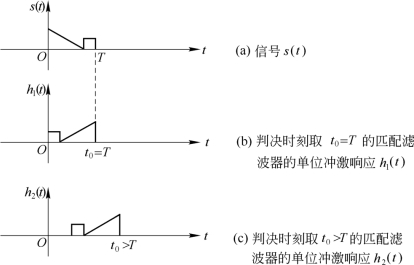
图7.3.2 匹配滤波器的单位冲激响应h(t)与匹配信号s(t)
值得注意的是,一个物理可实现的系统,应该是因果系统,因此就要有:当t＜0时,h(t)=0,也就是有当t0＜t时,s(t)=0,这说明对于物理可实现的匹配滤波,发送信号s(t)必须在匹配滤波器输出最大信噪比时刻t0到来之前消失为零。从物理意义上可以理解为,发送信号未结束,就不能得到信号的全部能量E,因而也不能得到最大信噪比。一般希望t0尽量的小,所以常把发送信号持续时间的末尾取作判决时刻t0。如图7.3.2(b)所示,取t0=T。由此可得匹配滤波器结构如图7.3.3所示。
图7.3.3 匹配滤波器结构
(3)匹配滤波器的输出s0(t)
因为匹配滤波器是线性滤波器,因此发送信号s(t)经该滤波器的输出为
从式(7.3.9)可以看出,匹配滤波器的输出信号与输入信号的自相关函数成比例,且在t=T时,有:s0(T)=KR(0)为最大。
在数字通信中,s(t)是(0,T)上的时间受限信号,接收信号是y(t),因此,匹配滤波器的输出为
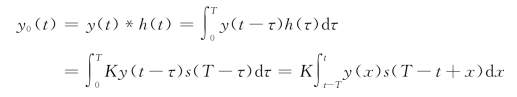
取判决时刻为t=T,代入上式,得
由以上推导可得出这样的结论:匹配滤波器可以用另一种形式表示,与式(7.2.23)相比较可以看出,匹配滤波器实质上是相关器,其结构如图7.3.4所示。可以用相关器来等效匹配滤波器,这里取K=1。
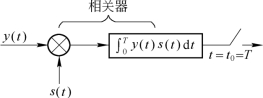
图7.3.4 匹配滤波器的结构
例7.3.1 已知信号s(t)=U(t)-U(t-T),如图7.3.5(a)所示。试分别画出t0=T和t0=1.5T的匹配滤波器单位冲激响应和输出波形,取K=1。
解 匹配滤波器单位冲激响应h(t)为
t0=T时,h1(t)=s(T-t)=U(t)-U(t-T),如图7.3.5(b)所示。
t0=1.5T时,h2(t)=s(1.5T-t)=U(t-0.5T)-U(t-1.5T),如图7.3.5(d)所示。
通过匹配滤波器h1(t)的输出为
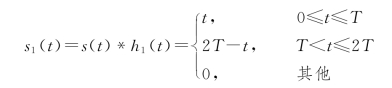
波形如图7.3.5(c)所示。
通过匹配滤波器h2(t)的输出为
波形如图7.3.5(e)所示。
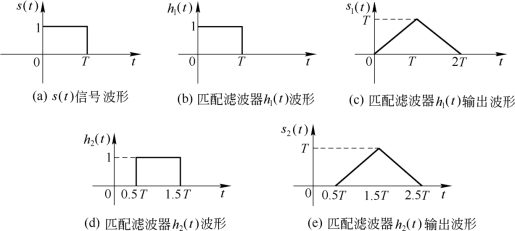
图7.3.5 匹配滤波器单位冲激响应和输出波形
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
