随信号的最佳接收方案优化：

假设接收端收到的两个等概率出现的随相信号为

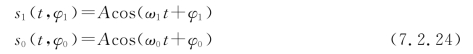
式中,ω1、ω0是使两个余弦信号互不相关的载频;φ1、φ0是随机相位变量,它们在观察周期(0,T)上(T是码元周期)取值从0～2π,且服从均匀分布;两个信号有相等的能量,即

因此,在接收端收到的信号为

(1)求解发送s1(t)或s0(t)时,接收信号的似然函数f(y|s1)和f(y|s0)

要利用最小差错概率准则建立最大似然函数结构的接收机,就必须先求出接收信号的似然函数。仔细分析现在的随相信号与前面确知信号的不同,就会发现随相信号似然函数不仅有发送信号这个条件,还多了一个随机相位变量的条件。由式(7.2.6)可以得到

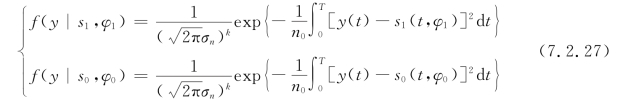
由第2章式(2.2.4),可以得到接收信号y和随机相位φ的联合概率密度函数

根据假设,φ1、φ0在(0,2π)内服从均匀分布,因此,求边际概率分布,就可以得到接收信号的似然函数f(y|s1)和f(y|s0):

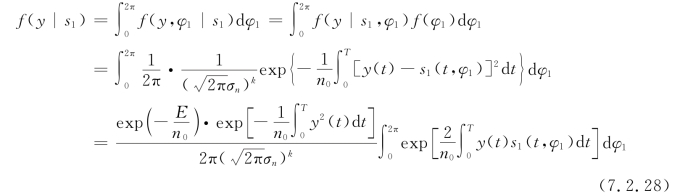
设

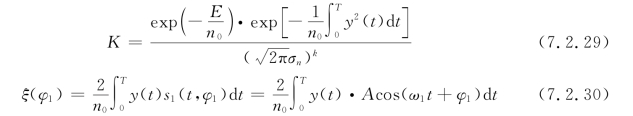
将式(7.2.29)和式(7.2.30)代入式(7.2.28),得

下面来研究式(7.2.30)。

设

(www.xing528.com)

将式(7.2.33)代入式(7.2.32),则

其中,

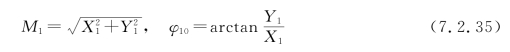
将式(7.2.34)代入式(7.2.31),得

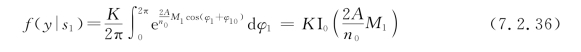
同理可以求得

在式(7.2.36)和式(7.2.37)中,I0(u)是零阶修正贝塞尔函数,

(2)用最大似然函数准则构建随相信号最佳接收机

依据最大似然函数准则,比较式(7.2.36)和式(7.2.37),谁大判谁。即

通过比较,可以发现,对似然函数的比较,可以转化为对零阶修正贝塞尔函数的比较;而又因零阶修正贝塞尔函数的单调增特性,可以将对零阶修正贝塞尔函数的比较,变为对M1和M0的比较,即

由式(7.2.41),就可以构建二进制随相信号最小差错概率准则下的最佳接收机,如图7.2.5所示。

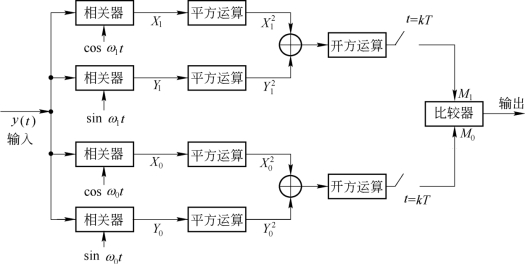
图7.2.5　二进制随相信号最小差错概率准则下的最佳接收机

同理,可以推出m进制随相信号最小差错概率准则下的最佳接收机如图7.2.6所示。

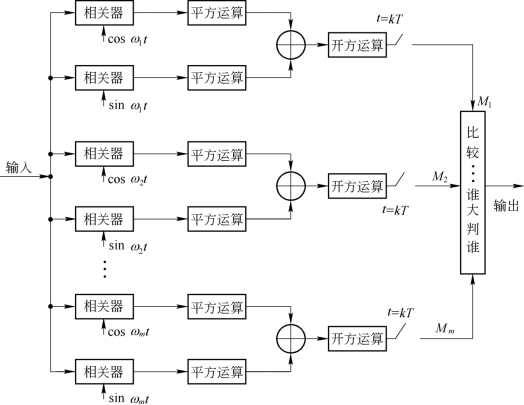
图7.2.6　m进制随相信号最小差错概率准则下的最佳接收机