最小化差错率的最佳接收机设计

在数字通信系统中,差错概率(即误码率)是衡量其质量的指标,因此,让差错概率最小就成为最直接的准则。参照这样的准则设计的接收机称为最小差错概率的最佳接收机。

1.最小差错概率准则

假设研究的是二进制的数字通信系统,发送的消息只有两种x1=1,x0=0,相应的发送信号也只有两种:s1对应x1,s0对应x0,在观察时刻对s1和s0的抽样分别为a1和a0。因此,发送信号为s1或s0时,接收信号为

接收信号y(t)在观察时刻的似然函数根据式(7.2.6)分别为

以上两个似然函数曲线如图7.2.2所示。

图7.2.2　二进制数字通信系统接收似然函数曲线

由图7.2.2可以看出,如果假设判决门限设定为V,则接收信号y(t)判决如下:

因此,发s1却被判为s0的错误概率P(s0|s1)和发s0却被判为s1的错误概率P(s1|s0)为

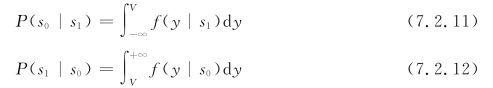
P(s0|s1)是图7.2.2中左边阴影的面积,P(s1|s0)是图7.2.2中右边阴影的面积。

由式(7.2.11)和式(7.2.12)可以得到二进制数字通信系统的平均差错概率为

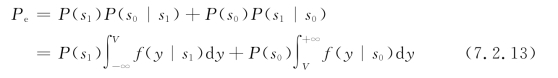
式中,P(s1)和P(s0)分别为发送s1和s0的概率,一般可以事先得到,是已知的。因此,在式(7.2.13)中,影响平均差错概率Pe的只有门限V,选择一个使Pe最小的最佳门限,就成为能否实现最佳判决的关键。为使Pe最小,对式(7.2.13)进行求导,令其为零,从而求出最佳门限V0。

由式(7.2.14)知,最佳判决时必须满足:

因此,当y＞V0,判为s1时,从图7.2.2和式(7.2.14)可得

同理,当y＜V0,判为s0时,从图7.2.2和式(7.2.14)可得

由式(7.2.15)、(7.2.16)和(7.2.17)可得到,满足最小差错概率准则的判决规则为

常称式(7.2.18)中不等号左边两个似然函数之比为似然比。(www.xing528.com)

当发送端信源两信号s1和s0的发送概率相等,即P(s1)=P(s0)=1/2时,式(7.2.18)可简化为

此判决规则习惯上称为最大似然判决法则。就是在收到接收信号y后,分别带入求解两个似然函数,哪个大就判大的那个对应的发送信号。

可以将最大似然法则推广到m进制的数字系统去,在发送m个等概率信号时,由最小差错概率准则得到的最大似然判决法则如下:

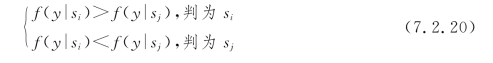
式中,i=1,2,…,m;j=1,2,…,m;i≠j。

2.最佳接收机结构

由最小差错概率准则的判决法则式(7.2.18),可以得到最佳接收机结构。

将式(7.2.6)代入式(7.2.18),则有

即:左大于右,则判收到的是s1;左小于右,则判收到的是s2。对式(7.2.21)整理、取对数,再整理,得

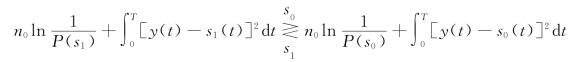
将中括号展开,并假设有

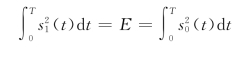
即发送信号等能量。令

判决规则整理成为

依据式(7.2.22),画出满足最小差错概率准则的最佳接收机结构如图7.2.3(a)所示。当发送信号等概率时,U1=U0,判决规则式(7.2.22)可以简化为

最佳接收机结构也可以简化为如图7.2.3(b)所示的形式。

由图7.2.3可见,接收机是依据y(t)与s1(t)或s0(t)的乘积、再积分这样的相关运算来构造的,因此也称该结构的接收机为相关检测器或相关性接收机。图中积分是在一个码元周期内进行的,比较器是对积分结束的kT时刻的抽样值进行比较,上支路大于下支路则判收到s1,反之判收到s0。需要注意的是,抽样后应立即对积分器清零,为下一次积分做好准备。

此外,还可以将发送信号的种类从2个增加到m个,当发送m种等概率信号时,最小错误概率准则下的最大似然判决最佳接收机如图7.2.4所示。

图7.2.3　最小差错概率准则的二进制最佳接收机

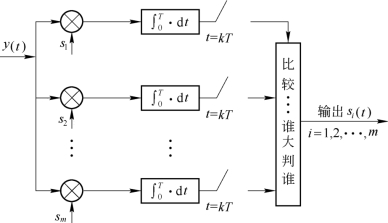
图7.2.4　发送m种等概率信号时,最小差错概率下的最大似然准则最佳接收机