数字信号接收的统计模型解析

在通信系统中,发送端所发的信号对接收端来说是不确定的,从信息论的概念来看,也正是因为不确定才有意义。而由于这些不确定,就要用统计学的方法来研究问题。为此可以建立一个数字通信系统的统计模型,如图7.2.1所示。

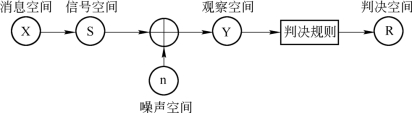
图7.2.1　数字通信系统的统计模型

在图7.2.1中,消息空间、信号空间、噪声空间、观察空间、判决空间分别代表着发送的消息、发送的信号、信道引入的噪声、接收端收到的波形和最终判决的所有可能状态的集合。

(1)消息空间:设有一个m种消息的离散信源,

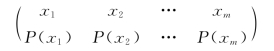
式中,P(xi)是消息xi发生的概率,i=1,2,…,m,因此有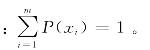

(2)信号空间:将消息变换为与其一一对应的信号,以便传输。用信号si表示消息xi,因此信号空间的信号也有m种,可以表示为

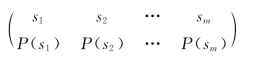
且有P(si)=P(xi),i=1,2,…,m和

(3)设在传输中引入的是加性零均值高斯白噪声n(t),功率谱密度为n0/2,它在抽样点上所得的样值为相互独立的随机变量,且具有相同的高斯分布规律,均值都为零,方差也都等于高斯白噪声n(t)的方差σ2n。因此,在一个码元周期(0,T)的观察区间上的k个噪声样值随机变量n1,n2,…,nk的k维联合概率密度函数f(n)为

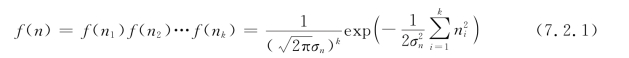
假设所发信号的最高截止频率为fm,理想的抽样频率为2fm,因此,在(0,T)观察时间上共抽取了2fmT个样值,其平均功率为

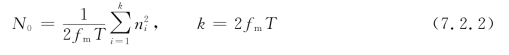
用Δt表示抽样间隔:Δt=,在Δt≪T时,式(7.2.2)可以表示为积分的形式:(www.xing528.com)

先整理式(7.2.1),再代入式(7.2.3),得

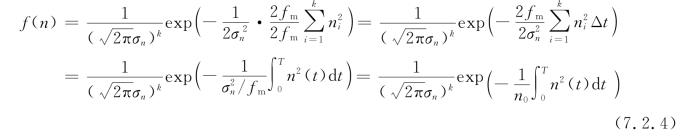
式中,n0=σ2n/fm是噪声的单边功率谱密度。

(4)在观察空间里,接收信号y(t)是信号空间的某一确知信号si(t)(但不知是哪一个,要判决的正是这一点)与噪声n(t)的和,即

因为n(t)是高斯过程,si(t)是确知信号,因此,y(t)也是一均值为si(t)、方差为σ2n的高斯过程。由此可以看出,发送信号为si(t)时,接收信号y(t)的条件概率密度函数为

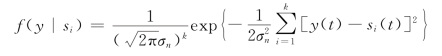
将式(7.2.5)代入上式,得

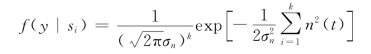
将式(7.2.4)代入上式,得

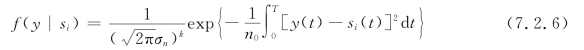
称式(7.2.6)的概率密度函数f(y|si)为似然函数。

(5)依据接收信号y(t)的统计特性,在相应的判决准则之下,就可以在判决空间中进行正确的判决。显然,判决空间中的元素r1,r2,…,rm,应与消息空间的消息x1,x2,…,xm一一对应。