多进制数字的相位调制方法优化

多进制数字相位调制又称多相制,是二相制的推广。它用多个相位状态的正弦振荡分别代表不同的数字信息。通常,相位数用M=2n计算,有2、4、8、16相制等(n分别为1、2、3、4等)M种不同的相位,分别与n位二进制码元的不同组合(简称n比特码元)相对应。多相制也有绝对相移MPSK和相对相移MDPSK两类。

多相制信号可以看作M个振幅及频率相同、初相不同的2ASK信号之和,当已调信号码元速率不变时,其带宽与2ASK、MASK及二相制信号是相同的。此时信息速率与MASK相同,是2ASK及二相制的log2M倍。可见,多相制是一种频带利用率较高的高效率传输方式,再加之有较好的抗噪声性能,因而得到广泛的应用,而MDPSK比MPSK用得更广泛一些。

设载波为cosωct,相对于参考相位的相移为φk,则M相制调制波形可表示为

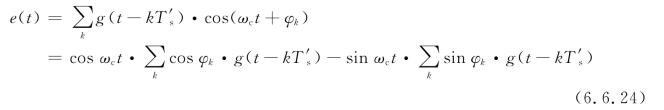
式中,g(t)是高度为1、宽度为T′s的门函数。

由于一般都是在0～2π范围内等间隔划分相位的,因此相邻相移的差值为

令

且

这样式(6.6.24)变为

可见,多相制信号可等效为两个正交载波进行多电平双边带调制所得信号之和。这样,就把数字调相和线性调制联系起来,给M相制波形的产生提供了依据。

根据以上的分析,相邻两个相移信号的矢量偏移为2π/M。但是,用矢量表示各相移信号时,其相位偏移有两种形式。如图6.6.4所示,它就是相位配置的两种形式。图中注明了各相位状态所代表的n比特码元,虚线为基准位(参考相位)。对绝对相移而言,参考相位为载波的初相;对差分相移而言,参考相位为前一已调载波码元的末相(当载波频率是码元速率的整数倍时,也可认为是初相)。各相位值都是对参考相位而言的,正为超前,负为滞后。两种相位配置形式都采用等间隔的相位差来区分相位状态,即M进制的相位间隔为2π/M,这样造成的平均差错概率将最小。图6.6.4所示的形式一称为π/2体系,形式二称为π/4体系。两种形式均分别有2相、4相和8相制的相位配置。

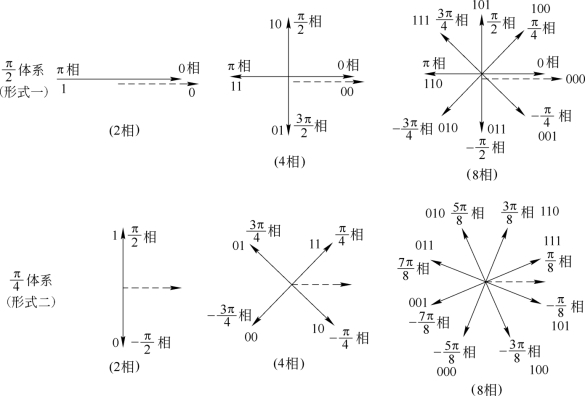
图6.6.4　相位配置矢量图

图6.6.5是四相制信号的波形图。图中示出了4PSK的π/4及π/2配置的波形和4DPSK的π/4及π/2配置的波形图。图中的T′s是四进制码元的周期,一个T′s周期是由两个二进制比特数构成的。载波周期在这里选取与四进制码元周期相等。

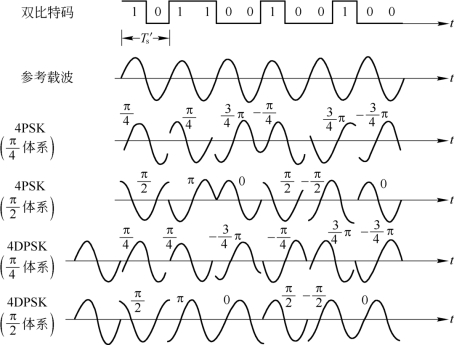
图6.6.5　四相制信号波形图

多相制信号中最常用的是4PSK,又称QPSK,还有8PSK信号。这里着重介绍四相制。产生多相制信号常用的方法有三种:直接调相法、相位选择法及脉冲插入法。

(1)直接调相法

①4PSK信号的产生(π/4体系)

4PSK常用正交调制法来直接产生调相信号,其原理方框图如图6.6.6(a)所示,它属于π/4体系。二进制数码两位一组输入,习惯上把双比特的前一位用A代表,后一位用B代表。经串/并变换后变成宽度为二进制码元宽度两倍的并行码(A、B码元时间上是对齐的)。再分别进行极性变换,把单极性码变成双极性码(0变为-1,1变为+1),如图6.6.6(b)中I(t)、Q(t)波形所示。然后分别与互为正交的载波相乘,两路乘法器输出的信号是互相正交的双边带调制信号,其相位与各路码元的极性有关,分别由A、B码元决定,见图6.6.6(a)中的矢量图。经相加电路(也可看作是矢量相加)后输出两路的合成波形,对应的相位配置见4PSK的π/4体系矢量图。

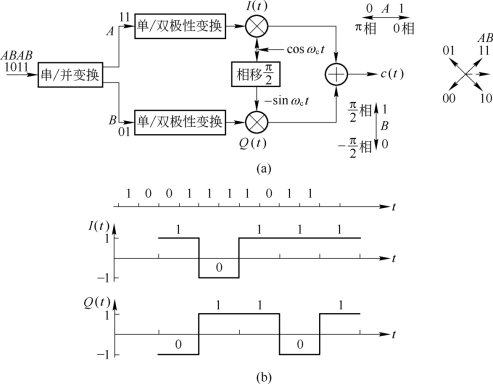
图6.6.6　直接调相法产生4PSK信号方框图及码变换波形

若要产生4PSK的π/2体系,只需适当改变相移网络就可实现。

②4DPSK信号的产生(π/2体系)

在直接调相的基础上加码变换器,就可形成4DPSK信号。图6.6.7示出了4DPSK的π/2体系信号方框图。图中的单/双极性变换的规律与4PSK情况相反,即0变为+1,1变为-1,相移网络也与4PSK不同,其目的是要形成π/2体系矢量图。图中的码变换器比差分编码器复杂得多,但可以用数字电路实现。

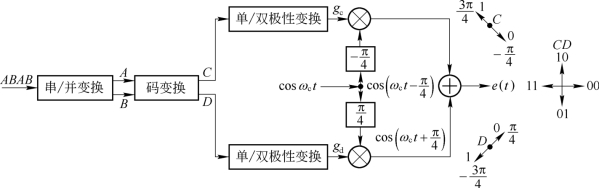
图6.6.7　直接调相法产生4DPSK信号的方框图

③8PSK信号的产生(π/4体系)

8PSK调制器方框图如图6.6.8所示。输入二进制信号序列经串/并变换每次产生一个3bit的码组b1b2b3,因此符号率为比特率的1/3。在b1b2b3控制下,同相路和正交路分别产生四电平的基带信号I(t)和Q(t)。b1用于决定同相路信号的极性,b2用于决定正交路信号的极性,b3则用于确定同相路和正交路信号的幅度。不难算出,若8PSK信号幅度为1,则b3=1时同相路基带信号幅度为0.924,而正交路幅度为0.383;b3=0时同相路幅度为0.383,而正交路幅度为0.924。因此,同相路与正交路的基带信号幅度是互相关联的,不能独立选取。例如,当3比特二进制序列b1b2b3=101时,同相路b1b3=11,其幅度在水平方向为+0.924,正交路b2b3=01,这时的正交路产生的幅度在垂直方向为-0.383。将这两个幅度不同而互相正交的矢量相加,就可得到幅度为1的矢量101,其相移为-π/8。

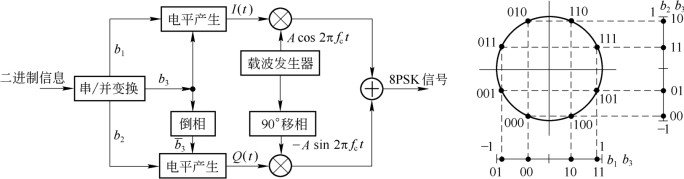(www.xing528.com)

图6.6.8　8PSK正交调制器(π/4体系)

(2)相位选择法

直接用数字信号选择所需相位的载波以产生M相制信号。4PSK的方框图见图6.6.9。在这种调制器中,载波发生器产生四种相位的载波,经逻辑选相电路根据输入信息每次选择其中一种相移的载波作为输出,然后经带通滤波器滤除高频分量。显然这种方法比较适合于载频较高的场合,此时,带通滤波器可以做得很简单。

若逻辑选相电路还能完成码型变换的功能,就可形成4DPSK信号。

图6.6.9　相位选择法产生四相制信号方框图

(3)脉冲插入法

图6.6.10所示是脉冲插入法方框图,它可实现π/2体系相移。主振频率为4倍载波频率的定时信号,经两级二分频输出。输入信息经串/并变换逻辑控制电路,产生π/2推动脉冲和π推动脉冲。在π/2推动脉冲作用下,第一级二分频电路相当于分频链输出提前π/2相位;在π推动脉冲作用下,第二级二分频多分频一次,相当于提前π相位。因此可以用控制两种推动脉冲的办法得到不同相位的载波。显然,分频链输出也是矩形脉冲,需经带通滤波才能得到以正弦波作为载波的QPSK信号。用这种方法也可实现4DPSK调制。

图6.6.10　脉冲插入法原理方框图

下面介绍几种具有代表性的多相制信号的解调方法。

(1)相干正交解调(极性比较法)

这里介绍4PSK(QPSK)信号的解调方法,其相干解调器如图6.6.11所示。因为4PSK(π/4体系)信号是两个正交的2PSK信号合成的,因此,可仿照2PSK相干检测法,在同相路和正交路分别设置两个相关器,即用两个相互正交的相干信号分别对两个二相信号进行相干解调,得到I(t)和Q(t),再经电平判决和并/串变换即可恢复原始数字信息。此法也称为极性比较法。

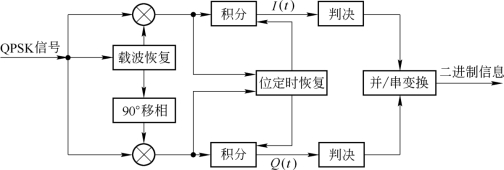
图6.6.11　QPSK信号的相干解调

(2)差分正交解调(相位比较法)

对于4DPSK信号往往使用差分正交解调法。多相制差分调制的优点就在于它能够克服载波相位模糊的问题。因为多相制信号的相位偏移是相邻两码元相位的偏差,因此,在解调过程中,也可同样采用相干解调和差分译码的方法。

4DPSK的解调是仿照2DPSK差分检测法,用两个正交的相干载波,分别检测出两个分量A和B,然后还原成二进制双比特串行数字信号。此法也称为相位比较法。

解调4DPSK(π/2体系)信号的方框图如图6.6.12所示。由于相位比较法比较的是前后相邻两个码元载波的初相,因而图中的延迟和相移网络以及相干解调就完成了π/2体系信号差分正交解调的过程,且这种电路仅对载波频率是码元速率整数倍时的4DPSK信号有效。

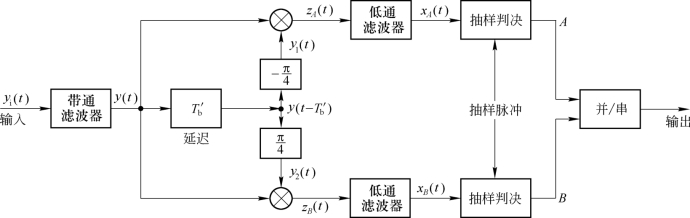
图6.6.12　4DPSK信号的解调方框图

(3)8PSK信号的解调

8PSK信号也可采用相干解调器,区别在于电平判决由二电平判决改为四电平判决。判决结果经逻辑运算后得到了比特码组,再进行并/串变换。通常使用的是双正交相干解调方案,如图6.6.13所示。此解调器由两组正交相干解调器组成,其中一组参考载波信号相位为0和π/2;另一组参考载波信号相位为-π/4和π/4。四个相干解调器后接四个二电平判决器,对其进行逻辑运算后即可恢复出图6.6.8中的b1、b2、b3,然后进行并/串变换,得到原始的串行二进制信息。图中载波φ=0对应cosωct;载波φ=-π/4对应着cos(ωct-π/4),c1、c2、c3、c4就是这两个相干载波的移相信号,也就是上面所说的二组参考载波的四个相移信号。

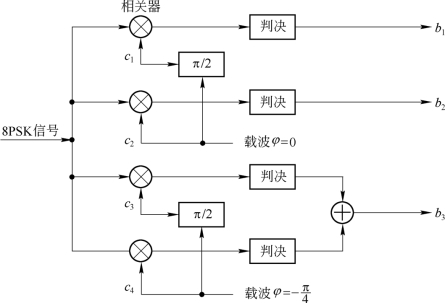
图6.6.13　8PSK信号的双正交相干解调

通过计算可得MPSK及MDPSK的误码率公式。对于MPSK信号,若采用相干解调器,可计算出系统总的误码率为

式中,r为接收信噪比。对于MDPSK方式的误码率为

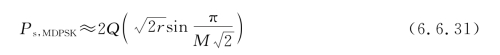
MPSK和MDPSK采用相干解调时的误码率性能曲线如图6.6.14所示。图中实线为MPSK,虚线为MDPSK。当采用格雷码时,误比特率与误码率之间的关系如下

由以上结论和图6.6.14可以看出,当误码率一定时,M越大则所要求的接收信噪比r就越大;当接收信噪比r一定时,M越大则误码率就越大;相同的M和误码率,MDPSK比MPSK所要求的接收信噪比r要大,即当M很大时,差分移相和相干移相比较大约损失3dB的功率。当M=4时,大约损失2.3dB的功率。

图6.6.14　MPSK和MDPSK相干解调时的误码率性能曲线