提升二进制频移键控系统性能的方法

1.相干解调时系统的误比特率

2FSK信号相干解调抗噪声性能的分析方法和2ASK信号相干解调时很相似,而且得到的结论也相似。将2FSK信号表示为

当发送数字信号为1,即2FSK信号的载波频率为ω1时,信号能通过上支路的带通滤波器,带通滤波器的输出是信号和窄带噪声的叠加,即

则低通滤波器的输出为

式中未计入系数1/2。v1(t)的概率密度函数为

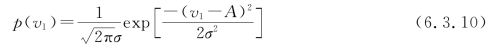
与此同时,信号Acosω1t不能通过下支路中的带通滤波器,于是下支路中的带通滤波器的输出就是窄带高斯噪声,即

低通滤波器的输出为

式中未计入系数1/2。v2(t)的概率密度函数为

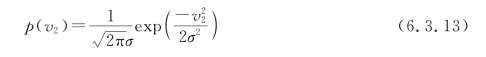
设v1(t)和v2(t)的差为v(t),可得

如果这个电压比零小,则判决器将产生一个错误。这样一个错误的概率就是v(t)＜0的概率。由于n1(t)和n2(t)都是均值为0,方差为σ2的高斯噪声,所以v(t)是均值为A、方差为σ2v=2σ2的高斯随机变量。v(t)的概率密度函数可写成

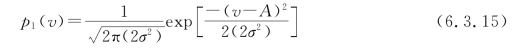
同理,当发送数字信号为0,即2FSK信号的载波频率为ω2时,也可得到类似的结果。这时的v(t)为

这种情况下可得到v(t)的概率密度函数为

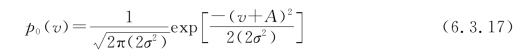
与分析2ASK信号同样的道理,只是这里最佳判决门限为0。当两种发送信号等概率,即P0=P1=1/2时,则2FSK的误比特率为

(www.xing528.com)

由于ω1和ω2相隔不远,它们的传输条件及接收条件类似,可认为两种情况下信号的错误概率相同,因此有

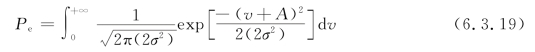
对式(6.3.19)进行变量代换,引入新变量z,令代入得

式中,r=为接收信噪比。将式(6.3.20)和(6.2.19)相比可知,当误比特率相同时,相干接收2FSK系统所要求的峰值信噪比要比相干接收2ASK系统低3dB。

2.非相干解调时系统的误比特率

用包络检波器代替图6.3.8中的相干解调器,就得到2FSK非相干解调的方框图,如图6.3.7所示。

参照2ASK非相干解调的分析方法,在传号及空号情况下,需要求出上、下两个支路中包络检波器输入端的概率密度函数。当收到频率为ω1的信号时,在上支路中带通滤波器的输出端是信号和窄带高斯噪声的叠加。上支路中包络检波器输入端的包络概率密度函数为莱斯分布,由式(6.2.21)有

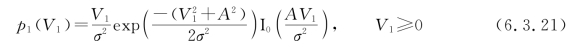
由于这个频率的信号不能通过下支路中的带通滤波器,因此在下支路只有噪声存在,则下支路中包络检波器输入端的包络概率密度函数为瑞利分布。由式(6.2.22)有

收到传号信号时,只有当V1＞V2才会有正确的判决,只要V1＜V2就会产生错误。在发送信号1和0等概率(即P1=P0=1/2)的条件下,由于传输条件和接收条件类似,可以认为在收传号时误判为空号的概率与收空号时误判为传号的概率相同。这样,非相干解调的2FSK的误比特率为

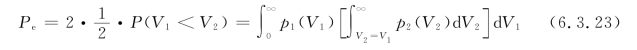
将式(6.3.21)和(6.3.22)代入上式,得

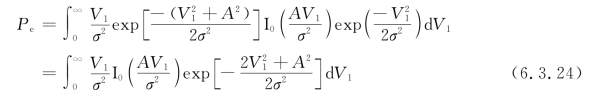
令x=,则上式可写为

引入这样一个结论:且设a=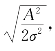则式(6.3.25)变为

式中的为接收信噪比。

将相干解调与包络(非相干)解调系统误码率做比较,可以发现:

①两种解调方法均可工作在最佳门限电平。

②在输入信号信噪比r一定时,相干解调的误码率小于非相干解调的误码率;当系统的误码率一定时,相干解调比非相干解调对输入信号的信噪比要求低。所以相干解调2FSK系统的抗噪声性能优于非相干的包络检测。但当输入信号的信噪比r很大时,两者的相对差别不明显。

③相干解调时,需要插入两个相干载波,因此电路较为复杂,但包络检测就无须相干载波,因而电路较为简单。一般而言,大信噪比时常用包络检测法,小信噪比时才用相干解调法,这与2ASK的情况相同。