二进制幅移键控系统的性能分析

1.相干解调时系统的误比特率

2ASK信号的相干解调如图6.2.5所示。为了求出相干接收时的误比特率,需要分别求出解调器输出的信号和噪声。为了讨论方便,将2ASK信号表示为

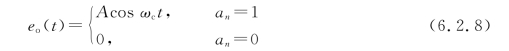
为简明起见,设信道传输没有损耗,在接收端收到的信号仍如式(6.2.8)所表示。

信道的高斯白噪声经带通滤波器后形成窄带高斯噪声,其表达式为

带通滤波器的输出是2ASK信号和窄带高斯噪声的叠加。当发送信号不为0时,带通滤波器的输出为

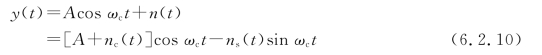
y(t)和相干载波相乘,然后由低通滤波器滤除高频分量。解调器输出为

式(6.2.11)中未计入系数1/2。由于nc(t)也是均值为0的窄带高斯噪声,其均方值即噪声功率为,所以x(t)是一个均值为A的高斯随机过程,其一维概率密度函数为

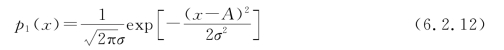
当发送信号为0时,解调器的输出只有噪声nc(t),x(t)的概率密度函数为

式(6.2.12)和式(6.2.13)所表示的概率密度曲线如图6.2.6所示,VT为判决门限值。

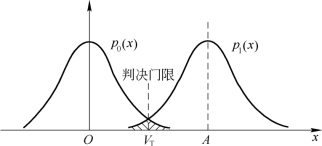
图6.2.6　概率密度曲线

由于噪声影响,发送端发送1信号,而接收端错判为0信号;或发送端发送0信号,而接收端错判为1信号,都会造成接收端发生误码。当两种发送信号等概率,即P0=P1=1/2时,平均误比特率为

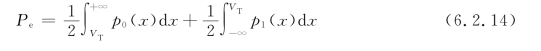
显然,最佳判决门限选在两条曲线的交点处,Pe最小,这时有

将式(6.2.12)和式(6.2.13)代入式(6.2.14)可计算Pe值。由图6.2.6可以看出,Pe就是图中阴影面积总和的一半,由于两块面积相等,Pe等于其中任意一块面积,因此有

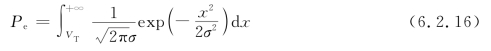
对式(6.2.16)进行变量代换,引入新变量z,令z=x/σ,则dz=dx/σ,将新变量z和式(6.2.15)代入式(6.2.16),得

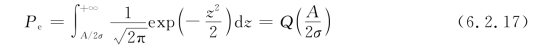
式中,Q(·)为Q函数(见附录C)。载波不为0时的2ASK信号称为峰值信号,解调器输入的信号功率为A2/2,噪声功率为σ2,则峰值信噪比为

r简称为接收信噪比。于是2ASK相干解调的误比特率又可表示为

2.非相干解调时系统的误比特率(www.xing528.com)

用一个包络检波器代替相干接收机中的相干解调器就构成了非相干接收机,如图6.2.4所示。求2ASK非相干接收系统的误比特率比相干接收系统要复杂得多,因为要先求出包络检波器输入端的包络概率密度函数。

白色高斯噪声经带通滤波器后变为窄带高斯噪声。窄带高斯噪声经包络检波非线性处理后,其抽样值已不是高斯分布。当发送信号不为0时,包络检波器的输入为余弦信号和窄带高斯噪声的叠加,即

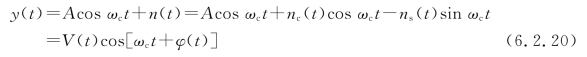
包络V(t)的概率密度函数呈莱斯分布,有

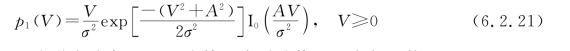
式中,A为信号幅度;σ2为噪声功率;I0(·)为第一类零阶修正贝塞尔函数。

当发送信号为0,即A=0时,输入端只有噪声存在,这时I0(0)=1,包络V的概率密度函数呈瑞利分布,有

p1(V)和p0(V)随V变化的曲线如图6.2.7所示,VT为判决门限值。

当两种发送信号等概率,即P0=P1=1/2时,平均误比特率为

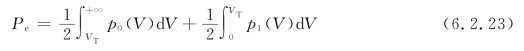
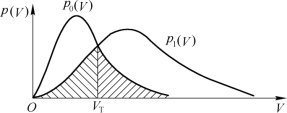
图6.2.7　包络值的概率密度曲线

最佳判决电平VT应在两条概率密度函数曲线的交点处,因此有

将式(6.2.21)和式(6.2.22)代入式(6.2.24)对VT求解,显然,要直接求解很困难,一个较好的近似解为

实际上,采用包络检波法的接收系统都应用在大信噪比的情况下,此时有VT≈A/2,而且具有近似关系

考虑到以上近似式,并将式(6.2.21)和式(6.2.22)代入式(6.2.23),可得

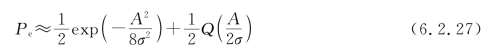
在信噪比很高的条件下,上式可进一步近似为

式中是接收信噪比。此时错误主要发生在发送信号为0的时候。

式(6.2.28)说明,对于2ASK非相干接收系统,在大信噪比及最佳判决门限时,误比特率随信噪比的增大而近似地按指数规律下降。

将2ASK信号非相干解调与相干解调相比较,可以得出以下几点结论:

(1)相干解调比非相干解调容易设置最佳判决门限电平。因为相干解调时最佳判决门限仅是信号幅度的函数,而非相干解调时最佳判决门限是信号和噪声的函数。

(2)最佳判决门限时,r一定,Pe相＜Pe非,即信噪比一定时,相干解调的误码率小于非相干解调的误码率;Pe一定时,r相＜r非,即系统误码率一定时,相干解调比非相干解调对信号的信噪比要求低。可见,相干解调2ASK系统的抗噪声性能优于非相干解调系统。这是由于相干解调利用了相干载波与信号的相关性,起了增强信号抑制噪声作用的缘故。

(3)相干解调需要插入相干载波,而非相干解调不需要。可见,相干解调时设备要复杂一些,而非相干解调时设备要简单一些。

一般而言,对2ASK系统,大信噪比条件下使用包络检测,即非相干解调;而小信噪比条件下使用相干解调。