扰码和解扰的原理简介

扰码原理是以线性反馈移位寄存器理论作为基础的。以5级线性反馈移位寄存器为例,在反馈逻辑输出与第一级寄存器输入之间引入一个模2和相加电路,以输入序列作为模2和相加电路的另一个输入端,即可得到图5.9.6(a)所示的扰码器电路,相应的解扰电路如图5.9.6(b)所示。

图5.9.6　5级移位寄存器构成的扰码器和解扰器

若输入序列{cn}是信源序列,扰码电路输出序列为{bn},则bn可表示为

经过信道传输,接收序列为,解扰电路输出序列为}可表示为

当传输无差错时,有,由式(5.9.20)和(5.9.21)可得,这说明扰码和解扰是互逆运算。

以图5.9.6构成的扰码器为例,假设移位寄存器的初始状态除an-5=1外其余均为0,设输入序列cn是周期为6的序列000111000111…,则各反馈抽头处an-3、an-5及输出序列bn如下所示:(www.xing528.com)

bn是周期为186的序列,这里只列出开头的一段。由此例可知,输入周期性序列经扰码器后变为周期较长的伪随机序列。如果输入序列中有连1或连0串时,输出序列也会呈现出伪随机性。如果输入序列为全0,只要移位寄存器初始状态不为全0,扰码器就是一个线性反馈移位寄存器序列发生器,当有合适的反馈逻辑时就可以得到m序列伪随机码。

扰码器和相应的解扰器的一般形式分别如图5.9.7(a),(b)所示。接收端采用的是一种前馈移位寄存器结构,可以自动地将扰码后的序列恢复为原始的数据序列。

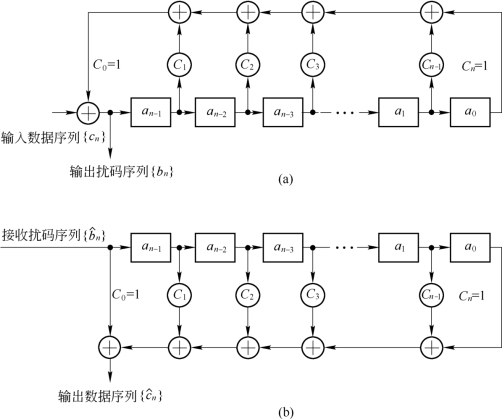
图5.9.7　扰码器和解扰器的一般形式

由于扰码器能使包括连0或连1在内的任何输入序列变为伪随机码,所以在基带传输系统中作为码型变换使用时,能限制连0码的个数。

采用扰码方法的主要缺点是对系统的误码性能有影响。在传输扰码序列过程中产生的单个误码会在接收端解扰器的输出端产生多个误码,这是因为解扰时会导致误码的增值。误码增值是由反馈逻辑引入的,反馈项数愈多,差错扩散也愈多。

m序列是周期的伪随机序列。在调试数字设备时,m序列可作为数字信号源使用。如果m序列经过发送设备、信道和接收设备后仍为原序列,则说明传输是无误的;如果有错误,则需要进行统计。在接收设备的末端,由同步信号控制,产生一个与发送端相同的本地m序列。将本地m序列与接收端解调出的m序列逐位进行模2加运算,一旦有错,就会出现1码,用计数器计数,便可统计错误码元的个数及比率。发送端m序列发生器及接收端的统计部分组成的成套设备称为误码测试仪。