如何生成和理解m序列

随机噪声在通信技术中首先是作为有损通信质量的因素受到人们重视的。在许多章节中都已指出,信道中存在的随机噪声会使模拟信号产生失真,或使数字信号解调后出现误码;同时,它还是限制信道容量的一个重要因素。因此,人们最早是企图设法消除或减小通信系统中的随机噪声。但是,有时人们也希望获得随机噪声。例如,在实验室中对通信设备或系统进行测试时,有时要故意加入一定的随机噪声,这时则需要产生它。

在20世纪40年代末,香农指出,在某些情况下,为了实现最有效的通信,应采用具有白噪声统计特性的信号。另外,为了实现高可靠的保密通信,也希望利用随机噪声。但是,利用随机噪声的最大困难是它难以重复产生和处理。直到60年代,伪随机噪声的出现才使这一困难得到解决。

伪随机噪声具有类似于随机噪声的一些统计特性,同时又便于重复产生和处理。由于它具有随机噪声的优点,又避免了随机噪声的缺点,因此获得了广泛的实际应用。被广泛应用的伪随机噪声都是由数字电路产生的周期序列得到的,这种周期序列称为伪随机序列。

通常产生伪随机序列的电路为一反馈移存器。它又可分为线性反馈移存器和非线性反馈移存器两类。由线性反馈移存器产生的周期最长的二进制数字序列称为最大长度线性反馈移存器序列,通常简称为m序列。由于它的理论比较成熟,实现比较简便,实际应用也较广泛,因此这里主要讨论m序列。

m序列是由带线性反馈的移位寄存器产生的序列,并且具有最长的周期。

由n级串接的移位寄存器和反馈逻辑线路可组成动态移位寄存器,如果反馈逻辑线路只用模2和构成,则称为线性反馈移位寄存器;如果反馈线路中包含“与”“或”等运算,则称为非线性反馈移位寄存器。

带线性反馈逻辑的移位寄存器设定初始状态后,在时钟触发下,每次移位后各级寄存器状态会发生变化。其中任何一级寄存器的输出,随着时钟节拍的推移都会产生一个序列,该序列称为移位寄存器序列。

以图5.9.2所示的4级移位寄存器为例,图中线性反馈逻辑服从以下递归关系式:

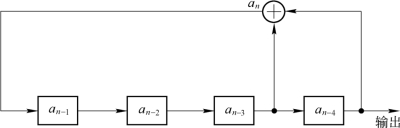
图5.9.2　式(5.9.13)对应的4级移位寄存器

即第3级与第4级输出的模2和运算结果反馈到第1级去。假设这4级移位寄存器的初始状态为0001,即第4级为1状态,其余3级均为0状态。随着移位时钟节拍,各级移位寄存器的状态转移流程图如表5.9.1所示。在第15节拍时,移位寄存器的状态与第0拍的状态(即初始状态)相同,因而从第16拍开始必定重复第1至第15拍的过程。这说明该移位寄存器的状态具有周期性,其周期长度为15。如果从末级输出,选择3个0为起点,便可得到如下序列:

表5.9.1　m序列发生器状态转移流程图

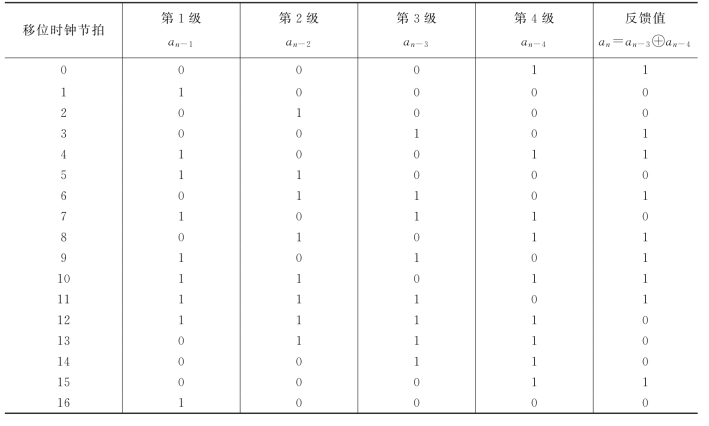
可以看出,对于n=4的移位寄存器共有24=16种不同的状态。上述序列中出现了除全0以外的所有状态,因此是可能得到的最长周期的序列。只要移位寄存器的初始状态不是全0,就能得到周期长度为15的序列。其实,从任何一级寄存器的输出所得到的序列都是周期为15的序列,只是节拍不同,这些序列都是最长线性反馈移位寄存器序列。

将图5.9.2中的线性反馈逻辑改为

如图5.9.3所示。如果4级移位寄存器的初始状态仍为0001,可得末级输出序列为

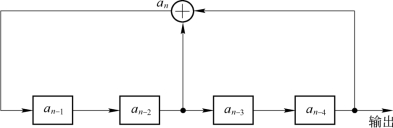
图5.9.3　式(5.9.14)对应的4级移位寄存器

其周期为6。如果将初始状态改为1011,输出序列是周期为3的循环序列,即

当初始状态为1111时,输出序列是周期为6的循环序列,其中一个周期为

以上4种不同的输出序列说明,n级线性反馈移位寄存器的输出序列是一个周期序列,其周期长短由移位寄存器的级数、线性反馈逻辑和初始状态决定。但在产生最长线性反馈移位寄存器序列时,只要初始状态非全0即可,关键要有合适的线性反馈逻辑。

n级线性反馈移位寄存器如图5.9.4所示。

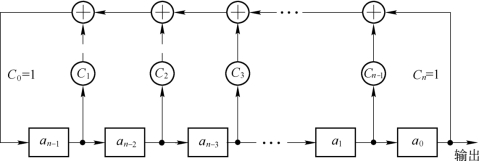
图5.9.4　n级线性反馈移位寄存器

图5.9.4中Ci表示反馈线的两种可能连接状态,Ci=1表示连接线接通,第n-i级输出加入反馈中;Ci=0表示连接线断开,第n-i级输出未参加反馈。因此,一般形式的线性反馈逻辑表达式为(www.xing528.com)

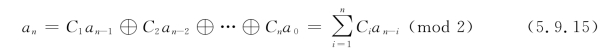
将等式左边的an移至右边,并将an=C0an(C0=1)代入上式,则上式可改写为

定义一个与式(5.9.16)相对应的多项式

式中,x的幂次表示元素相应的位置。式(5.9.17)称为线性反馈移位寄存器的特征多项式,特征多项式与输出序列的周期有密切关系。可以证明,当F(x)满足下列3个条件时,就一定能产生m序列:

(1)F(x)是不可约的,即不能再分解因式;

(2)F(x)可整除xp+1,这里p=2n-1;

(3)F(x)不能整除xq+1,这里q＜p。

满足上述条件的多项式称为本原多项式。这样,产生m序列的充要条件就变成如何寻找本原多项式了。以前面提到的4级移位寄存器为例。4级移位寄存器所能产生的m序列,其周期为p=24-1=15,其特征多项式F(x)应能整除x15+1。将x15+1进行因式分解,有

以上共得到5个不可约因式,其中有3个4阶多项式,而x4+x3+x2+x+1可整除x5+1,即

故不是本原多项式。其余2个是本原多项式,而且是互逆多项式,只要找到其中的一个,另一个就可写出。例如F1(x)=x4+x3+1就是图5.9.2对应的特征多项式,另一个F2(x)=x4+x+1是与其互逆的多项式。

表5.9.2　本原多项式系数表

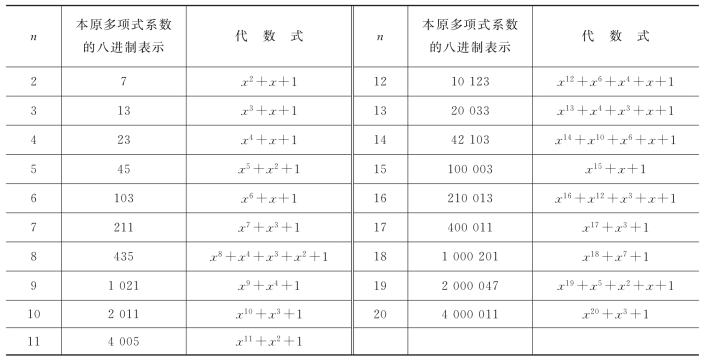
寻求本原多项式是一件烦琐的工作,计算得到的结果列于表5.9.2。表中给出其中部分结果,每个n只给出一个本原多项式。为了使m序列发生器尽量简单,常用的是只有3项的本原多项式,此时发生器只需要一个模2和加法器。但对于某些n值,不存在3项的本原多项式。表中列出的本原多项式都是项数最少的,为简便起见,用八进制数字表示本原多项式的系数,由系数写出本原多项式非常方便。例如n=4时,本原多项式系数的八进制数字表示为23,将23写成二进制数字010与011,从左向右第1个1对应于C0,按系数可写出F1(x);从右向左的第1个1对应于C0,按系数可写出F2(x),其过程如下:

F1(x)和F2(x)为互逆多项式。

m序列有如下性质:

(1)由n级移位寄存器产生的m序列,其周期为2n-1。

(2)除全0状态外,n级移位寄存器可能出现的各种不同状态都在m序列的一个周期内出现,而且只出现一次。因此,m序列中1和0的出现概率大致相同,1码只比0码多1个。

(3)在一个序列中连续出现的相同码称为一个游程,连码的个数称为游程的长度。m序列中共有2n-1个游程,其中长度为1的游程占1/2,长度为2的游程占1/4,长度为3的游程占1/8,依此类推,长度为k的游程占2-k。其中最长的游程是n个连1码,次长的游程是n-1个连0码。

(4)m序列的归一化自相关函数R(j)只有两种取值。对于周期为p的m序列有

式中,A、D分别是m序列与其j次移位的序列在一个周期中对应元素相同和不相同的数目。可以证明,一个周期为p的m序列与其任意次移位后的序列模2相加,其结果仍是周期为p的m序列,只是原序列某次移位后的序列。所以对应元素相同和不相同的数目就是移位相加后m序列中0和1的数目。由于一个周期中0比1的个数少1,因此j为非零整数时A-D=-1;j为零时A-D=p,这样可得到

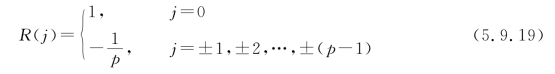
m序列的归一化自相关函数在j为整数的离散点上只有两种取值,所以它是一种双值自相关序列。R(j)是周期长度与m序列周期p相同的周期性函数。将归一化自相关函数的离散值用虚线连接起来,便得到图5.9.5所示的图形。

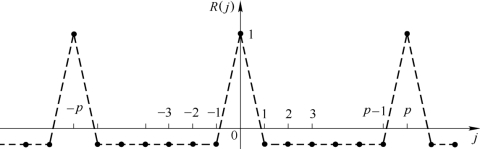
图5.9.5　m序列的归一化自相关函数

由以上特性可知,m序列是一个周期性确定序列,又具有类似于随机二元序列的特性,故常把m序列称为伪随机序列或伪噪声序列,记作PN序列。由于m序列有很强的规律性和伪随机性,因此得到了广泛的应用。