正交编码：数字通信技术中的重要技术

在数字通信技术中,正交编码是十分重要的技术。正交编码不仅可用做纠错码,而且可用来实现码分多址通信等。

先来看什么是正交。若两个周期为T的模拟信号s1(t)和s2(t)互相正交,那么

同理,若M个周期为T的模拟信号s1(t),s2(t),…,sM(t)构成一个正交信号集合,就有

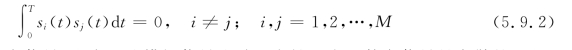
对于二进制数字信号,也有上述模拟信号这种正交性。由于数字信号是离散的,可以把它看成是一个码组,并且用一个数字序列来表示这一码组。这样的码组种类很多,这里只讨论码长相同的二进制码组集合。这时,两个码组的正交性可用互相关系数来表述。

设长为n的码组集合中码元取值为+1和-1,以及x和y是其中两个码组,即

式中,xi和yi取值为+1或-1,i=1,2,…,n,则x和y间的互相关系数定义为

若码组x和y正交,则必有ρ(x,y)=0。例如,图5.9.1所示的4个数字信号可以看作是如下4个码组:

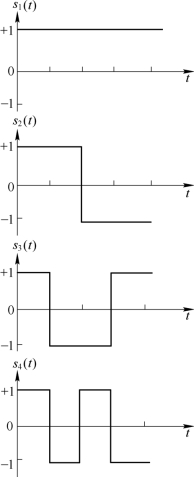
图5.9.1　正交编码信号

按式(5.9.5)计算可知,这4个码组中任意两者之间的相关系数都为零,也就是说这4个码组两两正交。这种两两正交的编码称为正交编码。

类似上述互相关系数的定义,还可以对于一个长为n的码组x定义其自相关系数为

式中,x的下标按模n运算,即有xn+k≡xk。(www.xing528.com)

在二进制编码理论中,经常采用二进制数字“0”和“1”表示码元的可能取值。这时,若规定用二进制数字“0”代替上述码组中的“+1”,用二进制数字“1”代替“-1”,则上述互相关系数定义式(5.9.5)将变为

式中,A为x和y中对应位码元相同的个数;D为x和y中对应位码元不同的个数。这样式(5.9.6)可以写成

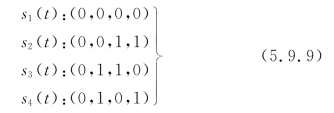
将其代入式(5.9.8),计算出的互相关系数仍为零。

式(5.9.8)中,若用x的j次循环移位代替y,就得到x的自相关系数ρx(j)。即令

代入式(5.9.8),就得到自相关系数ρx(j)。

有了正交编码的概念,可以引入超正交码和双正交码的概念。前面讲过,相关系数ρ的取值范围在±1之间。若两个码组间的相关系数ρ＜0,则称这两个码组互相超正交。

如果一种编码中任意两码组间都是超正交的,则称这种编码为超正交编码。例如,在式(5.9.9)中,若仅取后3个码组,并且删去其第一位,构成如下新的编码:

不难验证,由这3个码组所构成的编码是超正交码。

由正交编码和其反码便可以构成所谓双正交编码。例如,式(5.9.9)中正交码的反码为

式(5.9.9)和式(5.9.11)共同构成如下双正交码:

这种码中共有8种码组,码长为4,任两码组间的相关系数为0或-1。