时域均衡的原理解析

一般缺少信道的统计特性,所以很难设计最佳的有限长滤波器,通常利用一定形式的可调网络来实现。最有用的可变网络是横向滤波器。

当发送端发送单个脉冲时,由于系统传输特性不理想,接收端接收的信号波形会出现拖尾,在其他抽样时刻上的样值将不为0,即在nTs(n≠0)时刻会对其他码元进行串扰,如图5.8.1(a)中的实线所示。均衡的目的是要在其他抽样点上形成与拖尾相反的波形,如图5.8.1(a)中的虚线所示。均衡后得到图5.8.1(b)所示的波形,这样就不会形成码间串扰。

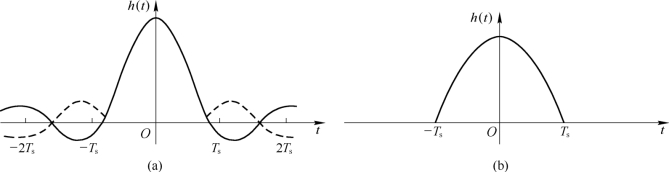
图5.8.1　均衡前后的波形

如果在未加入横向滤波器之前的基带传输系统的总传输特性不满足无码间串扰的条件,则在接收滤波器之后插入一个如图5.8.2所示的横向滤波器。它由带抽头的延迟线、加权系数为Cn的乘法器和加法器组成,每节延迟时间为码元周期Ts,共有2N个延迟单元,2N+1个抽头。每个抽头的加权系数分别为C-N,C-N+1,…,C-1,C0,C1,…,CN-1,CN,它们都是可调的。

当输入为单位冲激信号时,设均衡中心抽头处的响应波形为x(t),由图可知,均衡器的输出为

在抽样时刻t=kTs时,

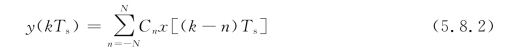
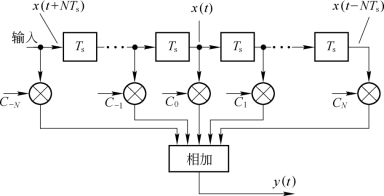
图5.8.2　横向滤波器

简写为

表明,均衡器输出波形在第k个抽样时刻得到的样值yk将由2N+1个值来确定,其中各个值是x(t)经过延迟后与相应的加权系数相乘的结果。对于有码间串扰的输入波形x(t),可以用选择适当的加权系数的方法,使输出y(t)在一定程度上减小码间串扰。设滤波器输出的波形如图5.8.3所示,除了y0以外,其余yk的值均属于波形失真引起的码间串扰。为了反映这些失真的大小,通常用峰值失真或均方失真作为度量标准。

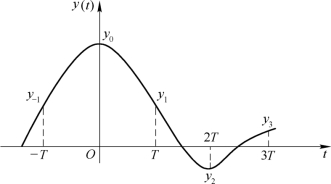
图5.8.3　有失真的冲激响应波形

峰值失真D定义为

式中,除k=0以外的各个样值绝对值之和反映了码间串扰的最大值,y0是有用信号的样值,所以峰值失真就是峰值码间串扰与有用信号样值之比,其比值愈小愈好。

同样也可将未均衡前的输入峰值失真表示为

均方失真定义为

它的物理意义与峰值失真类似。

根据式(5.8.4)和式(5.8.6)均可设计加权系数使失真最小,这两种设计准则分别称为最小峰值失真准则和最小均方失真准则。(www.xing528.com)

由最小峰值失真准则可知,峰值失真D是抽头系数C的函数。理论分析指出,当起始失真D0≤1时,调整2N个抽头系数CN,使2N个抽头的样值yk=0,这样能得到最小失真D。这时y(t)的2N+1个样值满足下式要求:

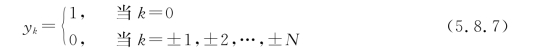
从这个结论出发,利用式(5.8.3)和式(5.8.7),列出2N+1个联立方程,可解出2N+1个抽头系数。将联立方程组用矩阵形式表示为

如果x-2N,…,x0,…,x2N已知,则求解上式线性方程组可以得到C-N,C-N+1,…,C-1,C0,C1,…,CN-1,CN2N+1个抽头系数值。使yk在k=0的两边各有N个零值的调整叫做“迫零”调整,按这种方法设计的均衡器称为“迫零”均衡器,此时D取得最小值,调整达到了最佳效果。

例5.8.1 已知输入信号的样值序列为x-2=0,x-1=0.2,x0=1,x1=-0.3,x2=0.1。试设计三抽头的“迫零”均衡器。求三个抽头的系数,并计算均衡前后的峰值失真。

解 因为2N+1=3,根据式(5.8.8),列出矩阵方程为

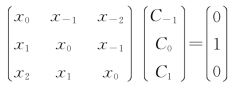
将样值代入上式,得

由矩阵方程可列出方程组

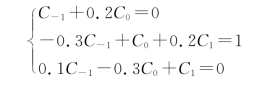
解联立方程组可得

再利用式(5.8.3)计算均衡器的输出响应,有

输入峰值失真为

输出峰值失真为

均衡后使峰值失真减小了7.5倍。

均衡前x(t)的波形和均衡后y(t)的波形分别如图5.8.4(a)、(b)所示。由图可以看出,在峰值两侧可以得到所期望的零点,但远离峰值上的一些抽样点上仍会有码间串扰。这是因为仅有3个抽头,只能保证样值两侧各一个零点。一般来说抽头有限时,总不能完全消除码间串扰,但当抽头数较多时可以将串扰减小到相当小的程度。

图5.8.4　例5.8.1中x(t)和y(t)的波形