多元码的差错率分析

多元码基带信号的幅度取值有多种选择。对M元码来说,每个码元周期内所发送的码元可以有M种幅度。一般来说,多元码是一种多进制传输信号,它并不限于是幅度电平的变化,也可以是载波频率、相位和别的变化。

通常M元码基带信号幅度电平的间隔是均匀的,为了排除直流功率的损耗,M种幅度电平的均值一般取为0。

以三元码为例,设相邻幅度间隔为A,则信号幅度选为-A、0、+A。若这三种幅度等概率出现,最佳判决电平选为-A/2、+A/2,则其幅度概率密度函数如图5.6.4所示。

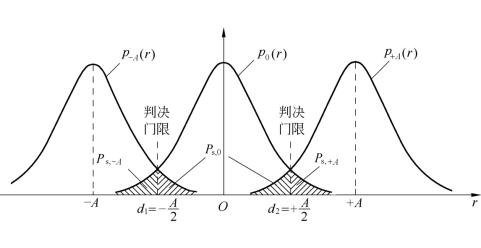
图5.6.4　三元码幅度概率密度函数

由图可知,-A电平发生错误判决的概率为

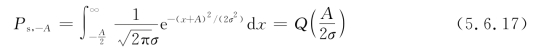
式中,σ2为加性高斯白噪声的方差。同理有

及

当时,可得总误码率为

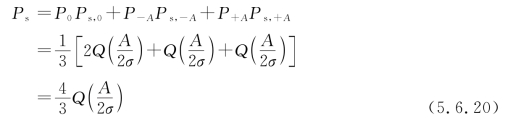
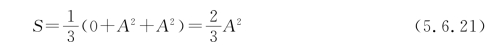
这样的三元码的信号功率为噪声功率为N=σ2。由式(5.6.20)可得

比较式(5.6.22)与式(5.6.16)知,要得到相同的误码率,需要的信号功率三元码要比双极性二元码的大,也就是说需要的信噪比三元码要比双极性二元码的大。

如果在某些三元码中三种幅度的出现概率不相等,最佳判决门限也不等于-A/2和A/2,那么误码率就不是式(5.6.22)了。例如,当AMI码的信码0、1等概率时,-A、0、+A三种幅度的出现概率分别为1/4、1/2、1/4,则判决门限应取为d1＞A/2、d2＜-A/2。这样Ps,-A、Ps,+A、Ps,0与式(5.6.17)、(5.6.18)、(5.6.19)都不一样,所以总误码率也不一样。

对于M元码来说,若M种幅度等概率出现,即每种幅度的出现概率为1/M,而且出现在不同时间的幅度是相互独立的,在加性高斯噪声影响下造成码元判决错误的概率为图5.6.4中所示阴影部分的面积。除了M个幅度中最高幅度和最低幅度以外,每个幅度都可能错判到上下两个方向的幅度上,所以涉及的阴影部分有2(M-1)个。于是,由式(5.6.20)可以推广到M元码误码率的一般表达式为

可见,如果幅度间隔A不变,误码率随着M的增大而缓慢增加。(www.xing528.com)

M元码有可能为奇数或偶数两种情况,其幅度取值不同。当M为偶数时,不同幅度值应选为

若它们等概率出现,则平均信号功率为

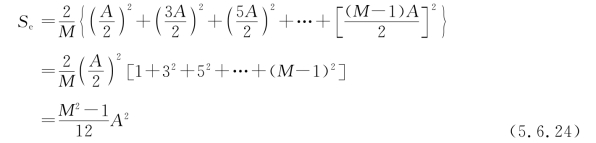
当M为奇数时,幅度值选为

它们等概率出现时的平均信号功率为

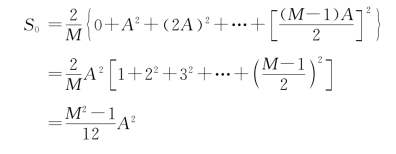
由式(5.6.24)和(5.6.25)可知,根据上述幅度选取原则,M元码的平均信号功率为

因此,M元码误码率可用信噪比表示为

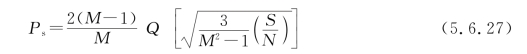
由于多元码的每个码元可以用来表示一个二进制码组,对于n位二进制码组来说,可以用M=2n元码来传输。与二元码传输相比,M元码传输时所需信道频带可降为而且由式(5.6.23)和(5.6.27)计算得到的是M元码的误码率,而不是二进制信码的误比特率。由此再来看M元码的误码率与二进制信码的误比特率之间的关系:由于M元码的二进制表示形式很多,所以误码率与误比特率之间的关系不是唯一的,必须结合二进制表示形式进行讨论。常用的二进制表示形式主要有普通二进制码和格雷码。

通过计算可得,当用普通二进制码表示时,二进制的误比特率Pb与M元码的误码率Ps之间的关系为

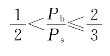
即误比特率略小于误码率。

采用格雷码时,二进制的误比特率Pb与M元码的误码率Ps之间的关系为

当n增大时,误比特率减小,与普通二进制码相比稍有改善,因此格雷码在多元码传输中得到广泛的应用。