部分响应波形分析

如果信号波形是具有持续1bit以上,且有一定长度码间干扰的波形,则称这种波形为部分响应波形。利用部分响应波形进行传送的基带传输系统称为部分响应系统。

部分响应信号波形的类型很多,一般常用的有五类部分响应波形。下面以第Ⅰ类部分响应波形为例来讨论一下其中的机理。

对相邻码元的取样时刻产生同极性串扰的波形,称为第Ⅰ类部分响应波形。为了推导表达式的方便,令前一个码元取样时刻在t=-T/2处,当前码元的取样时刻在T/2处,其余码元的取样时刻在±3T/2,±5T/2,…。用两个相隔一位码元间隔T的sinx/x的合成波形来代替sinx/x波形,如图5.5.1所示。合成波的数学表达式为

图5.5.1　第Ⅰ类部分响应信号

经数学变换后,得

由式(5.5.2)可知,s(t)的幅度约与t2成反比,而sinx/x的波形幅度与t成反比,因此波形拖尾的衰减速度加快了。从图5.5.1可以看出,相距一个码元间隔sinx/x波形的拖尾正负相反而相互抵消,使得合成波形拖尾迅速衰减。

对式(5.5.1)进行傅里叶变换,可以求出s(t)的频谱函数为

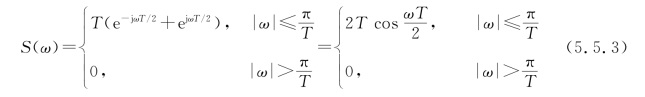
由式(5.5.3)画出的频谱函数如图5.5.1(b)所示。s(t)的频谱限制在±π/T之内,而且呈余弦型。这种缓变的滚降过渡特性与陡峭衰减的理想低通特性有明显的不同。此时的传输带宽为

频带的利用率为

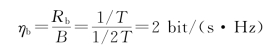
达到了基带传输系统在传输二元码时的理论最大值。

如果用s(t)作为传输信号的波形,在抽样时刻上,发送码元的样值将受到前一个发送码元的串扰,而对其他码元不会产生串扰。s(t)的形成过程可分为两步,首先形成相邻码元的串扰,然后再经过响应的网络形成所需的波形。通过有控制地引入串扰,使原先互相独立的码元变成了相关码元,这种串扰所对应的运算称为相关编码。

这种部分响应信号虽然解决了sinx/x波形的缺点,但它是以相邻码元抽样时刻出现一个与发送码元抽样值相同幅度的串扰作为代价的。由于存在这种固定幅度的串扰,使部分响应信号序列中出现新的抽样值,一般称它为伪电平。

设输入二进制信码序列为{an},并设an的取值为+1和-1,对应于二进制数字“1”和“0”,若采用这样的部分响应信号作为接收波形,它的抽样值将有-2、0、+2三种取值,即成为一种伪三元序列。因为发送信码为an时,接收波形在抽样时刻上的抽样值cn应是an与前一串扰值an-1之和,即cn=an+an-1。其形成过程可举例如下:

(www.xing528.com)

它的波形如图5.5.2所示。为简单起见,图中忽略了波形中的振荡部分。

在接收端,经过再生判决得到,再通过反变换得到an的估计值是前一码元的估计值。这样不断推算下去,显然,这种递推运算会带来严重的差错扩散问题。如果在传输过程中,{cn}序列中某个抽样值因干扰发生错误,不仅会造成当前恢复的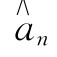值的错误,还会影响到以后所有的

图5.5.2　第Ⅰ类部分响应信号序列

差错传播的过程可举例如下:

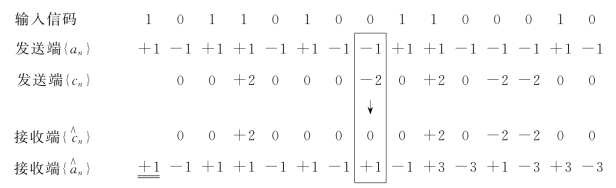
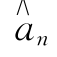可见,自{}出现错误之后,接收端恢复出来的{}全部是错误的。此外,在接收端恢复{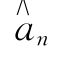}时还必须有正确的起始值(上例中第一个“+1”值),否则,即使没有传输差错也不可能得到正确的{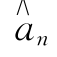}序列。

为了避免因相关编码而引起的差错传播问题,可以在发送端相关编码之前先进行预编码。对于单极性的二元码an,预编码的规则为

即

其中⊕为模2加。将bn转换为双极性二元码,然后再按以下规则进行相关编码,得

由式(5.5.4)和式(5.5.6)可得

由此式可知,预编码后的部分响应信号各抽样值之间已解除了相关性,由当前cn值可直接得到当前的an值。下面的例子说明了这一过程。

这里判决的规则为

由此例可知,当接收到的{}有错误时,恢复出来的{}中不发生错误传播现象,而只影响发生错误的这些位。