无码间干扰对传输条件的影响

首先假设传输系统中没有噪声,此时需要研究的就是在什么条件下,才会没有码间的干扰。在数字信号的传输过程中,码元波形是周期性发送的,信息携带在幅度上。接收端如果经过再生判决能准确地恢复出幅度信息,说明信码的传送是无误的。因此只需要研究在一些特定的时刻上无码间干扰的条件就可以了,并不要求波形在所有时间轴上都无延伸。

接收波形在特定时刻无码间干扰的充要条件是仅在本码元的抽样时刻上有最大值,而对其他码元抽样时刻的信号值无影响,也就是在抽样点上不存在码间干扰。对于一种典型的波形如图5.4.2所示,接收信号的抽样周期为T,接收波形s(t)除在t=0时抽样值为S0外,在t=kT(k≠0)的其他抽样时刻皆为0,因而不会影响其他抽样值。用数学表达式可以写为

其中,

只要满足上述关系,在抽样点上是无码间干扰的。

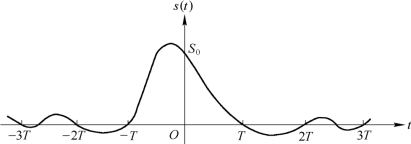
图5.4.2　抽样点上不存在码间干扰的波形

s(kT)是s(t)的一部分值,s(t)是经过基带系统后形成的波形。由于有

则可得到

当右边一致收敛时,求和与积分次序可以互换,则有

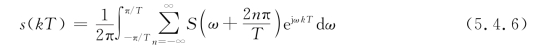
由傅里叶展开系数公式可知,s(kT)为的傅里叶展开系数。

由式(5.4.2)和式(5.4.6)得出在抽样时刻无码间干扰时,有

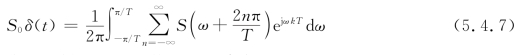
通过数学变换可以得到抽样时刻无码间干扰的充要条件为

即无码间干扰的基带传输特性应满足

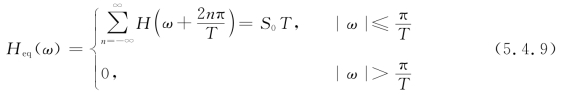
则基带系统的总特性H(ω)凡是能符合Heq(ω)要求的,均可消除码间干扰。这就为设计无码间干扰的基带系统提供了一个准则,称为奈奎斯特第一准则。

从式(5.4.9)很容易看出其物理意义,把传递函数在ω轴上以2π/T为间隔切开,然后分段沿ω轴平移到[-π/T,π/T]区间内,将它们叠加起来的结果应当为一常数,如图5.4.3所示。一般称为等效低通特性。(www.xing528.com)

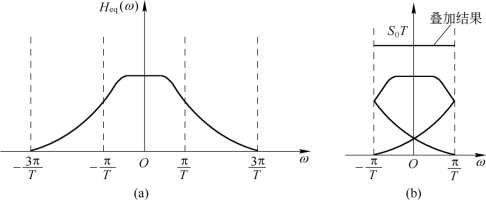
图5.4.3　Heq(ω)特性的构成

满足等效低通特性的传递函数有无数多种。通过分析可知,只要传递函数在±π/T处满足奇对称的要求,不管H(ω)的形式如何,都可以消除码间干扰。

以上是从抽样值无失真的条件出发得出的无码间干扰的准则。还有无失真恢复信码的另外一种办法,就是以一定电平对接收波形限幅,由此再生的脉宽正好等于码元间隔的矩形波。例如在图5.4.4中限幅电平为1/2抽样值。我们把判断信号幅度与限幅电平是否相等的判决时刻称为转换点。显然在其他转换点处串扰不应造成本来低于限幅电平的信号等于或超出限幅电平,即要求在其他转换点无串扰。这种基于转换点无失真的条件称为奈奎斯特第二准则。图5.4.4中例子的奈奎斯特第二准则的数学表示式为

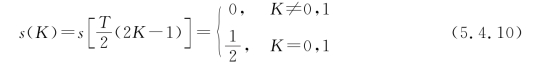
采用推导奈奎斯特第一准则过程中的类似办法,可以求出转换点无失真的充要条件为

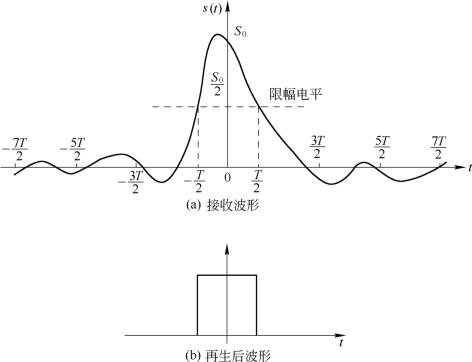
图5.4.4　满足转换点无失真条件的波形

此时的基带传输特性应满足

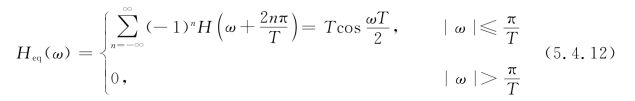
它的物理意义是把传递函数在ω轴上以2π/T为间隔切开,乘上符号因子(-1)n后分段平移到(-π/T,π/T)区间内,它们的叠加结果应为Tcos(τT/2),如图5.4.5所示。与奈奎斯特第一准则不同的是这里乘了一个符号因子(-1)n。

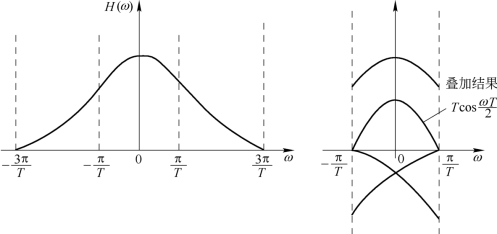
图5.4.5　满足转换点无失真条件的传输函数

如果传输函数在|ω|＞π/T时恒为0,则在|ω|≤π/T时必须有

才能满足转换点无失真的条件,这是一个特殊情况。

奈奎斯特第三准则表述为,如果在一个码元间隔内接收波形的面积正比于发送矩形脉冲的幅度,而其他码元间隔的发送脉冲在此码元间隔内的面积为零,则接收端也能无失真地恢复原始信码。

要满足这一准则,研究表明传递函数应为x/sinx函数的截短形式,其表达式为

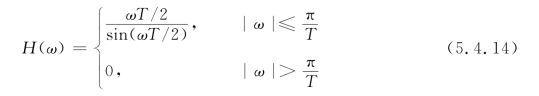
而它的冲激响应为